浙江省杭州市萧山区2023年九年级上学期数学期中试卷3

试卷更新日期：2023-12-20 类型：期中考试

进入出卷网下载

一、选择题（每小题3分，共30分）

1. 若 $\frac{a}{b} = \frac{2}{3}$ ，则 $\frac{a + b}{a}$ 的值是（）

A、2 B、 $\frac{1}{2}$ C、 $\frac{3}{2}$ D、 $\frac{5}{2}$

查看试题解析
2. 已知☉O的半径为5，点P在☉O外，则OP的长可能是（）

A、3 B、4 C、5 D、6

查看试题解析
3. 如图，两个三角形是位似图形，它们的位似中心是（）

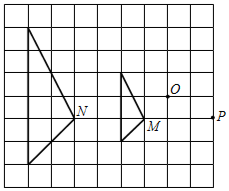A、点N B、点O C、点M D、点P

查看试题解析
4. 在△ABC中，∠C=90°，如果tanA= $\frac{3}{4}$ ，那么sinB的值等于（）

A、 $\frac{5}{3}$ B、 $\frac{3}{5}$ C、 $\frac{5}{4}$ D、 $\frac{4}{5}$

查看试题解析
5. 已知不透明的袋中只装有黑、白两种球，这些球除颜色外都相同，其中白球有30个，黑球有n个．随机地从袋中摸出一个球，记录下颜色后，放回袋子中并摇匀，再从中摸出一个球，经过如此大量重复试验，发现摸出的黑球的频率稳定在0.4附近，则n的值约为（）

A、20 B、30 C、40 D、50

查看试题解析
6. 如图，AB是半圆O的直径，AC、BC是弦，OD⊥AC于点D，若OD=1.5，则BC=（）

A、4.5 B、3 C、2 D、1.5

查看试题解析
7. 已知A=x²+a，B=2x，若对于所有的实数，A的值始终比B的值大，则a的值可能是（）

A、-1 B、0 C、1 D、2

查看试题解析
8. 如图，在 $△ A B C$ 中， $∠ C = 90 °$ ， $∠ B = 40 °$ ，将三角形ABC绕点A按顺时针方向旋转到三角形 $A B_{1} C_{1}$ 的位置，使得点 $C$ 、 $A$ 、 $B_{1}$ 在一条直线上，那么旋转角等于（）

A、145° B、130° C、135° D、125°

查看试题解析
9. 已知二次函数y=ax²+bx+c的图象如图所示，则下列结论中错误的是（）

A、a-b+c＞1 B、abc＞0 C、4a-2b+c＜0 D、c-a＞1

查看试题解析
10. 如图，在矩形ABCD中，AB=2，BC=4，P是对角线AC上的动点，连接DP，将直线DP绕点P顺时针旋转，使旋转角等于∠DAC，且DG⊥PG，即∠DPG=∠DAC．连接CG，则CG最小值为（）

A、 $\sqrt{5}$ B、 $\frac{6}{5}$ C、 $\frac{4}{5}$ D、 $\frac{36}{25}$

查看试题解析

二、填空题（每小题4分，共24分）

11. 已知抛物线y=ax²的开口向下，且|a|=3，则a= ．

查看试题解析
12. 已知点C为线段AB的黄金分割点（AC＞BC），已知AB＝2，则AC＝．

查看试题解析
13. 如图，已知AD是△ABC的中线，G为AD上一点，GF//BC且AG：GD=2：1，若△ABC的面积是12，则△AFG的面积是．

查看试题解析
14. 如图是由边长相同的小正方形组成的网格，A，B，P，Q四点均在正方形网格的格点上，线段AB，PQ相交于点E，则tan∠AEP= ．

查看试题解析
15. 在Rt△ABC中，∠ACB=90°，AC=3，BC=4，过点B作射线BM//AC．动点D从点A出发沿射线AC方向以每秒4个单位的速度运动，同时动点E点从点C沿射线AC方向以每秒3个单位的速度运动．过点E作EF⊥AC交射线BM于F，G是EF中点，连接DG．设点D运动的时间为t，当△DEG与△ACB相似时，t的值为．

查看试题解析
16. 已知函数y=x²-4ax+5(a为常数），当x≥4时，y随x的增大而增大．

(1)、实数a的取值范围为；

(2)、若P(x₁ ， y₁)，Q(x₂ ， y₂)是该函数图象上的两点，对任意的2a-1≤x₁≤5和2a-1≤x₂≤5，y₁ ， y₂总满足y₁-y₂≤5+4a² ，则实数a的取值范围是．

查看试题解析

三、解答题（共66分）

17. 将分别标有数字1，2，3的三张卡片洗匀后，背面朝上放在桌上，随机抽取一张作为十位上的数字（不放回），再抽取一张作为个位上的数字．

(1)、能组成哪些两位数？（请用树状图表示出来）

(2)、恰好是偶数的概率是多少？

查看试题解析
18.

(1)、求二次函数y=-2x²-4x+5的顶点坐标．

(2)、计算：2sin²45°+sin60°·tan30°-cos60°．

查看试题解析
19. 如图所示，有一圆弧形拱桥，其跨度AB=10m，拱高（圆弧中点到弦的距离）为1m．

(1)、请你用尺规确定圆弧所在圆的圆心；

(2)、求拱桥所在圆的半径长．

查看试题解析
20. 如图，某大楼的顶部竖有一块广告牌CD，小马同学在山坡的坡脚A处测得广告牌底部D的仰角为53°，沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°，已知山坡AB的坡比i=1： $\sqrt{3}$ ， AB=10米，AE=21米．（测角器的高度忽略不计，参考数据： $\sqrt{2}$ ≈1.41， $\sqrt{3}$ ≈1.73，sin53°≈ $\frac{4}{5}$ ， cos53°≈ $\frac{3}{5}$ ， tan53°≈ $\frac{4}{3}$ .）

(1)、求点B距水平地面AE的高度．

(2)、若市政规定广告牌的高度不得大于7米，请问该公司的广告牌是否符合要求，并说明理由．

查看试题解析
21. 如图，在△ABC中，∠C=90°，AC=3，CB=5，D是BC边上一点，且DB=1，点E是AC边上的一个点，且AE= $\frac{3}{5}$ ，过点E作EF//CB交AD于点F．

(1)、求EF的长．

(2)、求证：△DEF∽△ABD．

查看试题解析
22. 已知，点M为二次函数y=-x²+2bx-b²+4b+1图象的顶点，直线y=mx+5分别交x轴正半轴和y轴于点A，B．

(1)、判断顶点M是否在直线y=4x+1上，并说明理由；

(2)、如图1，若二次函数图象也经过点A，B，且mx+5＞-x²+2bx-b²+4b+1，结合图象，求x的取值范围；

(3)、如图2，点A坐标为(5，0)，点M在△AOB内，若点C( $\frac{1}{4}$ ， y₁)，D( $\frac{3}{4}$ ， y₂)都在二次函数图象上，试比较y₁与y₂的大小．

查看试题解析
23. 如图1，在△ABC中，AD⊥BC于点D，正方形PQMN的边QM在BC上，顶点P，N分别在AB，AC上，BC=a，AD=h．

(1)、求正方形PQMN的边长（用a和h的代数式表示）；

(2)、如图2，在△ABC中，在AB上任取一点P'，画正方形P'Q'M'N'，使Q'，M'在BC边上，N'在△ABC内，连接BN并延长交AC于点N，画NMBC于点M，画NP⊥NM交AB于点P，再画PQ⊥BC于点Q，得到四边形PQMN，证明四边形PQMN是正方形；

(3)、在（2）中的线段BN该线上截取NE=NM连接EQ，EM（如图3)，当∠QEM=90°时，求线段BN的长（用a，h表示）

查看试题解析