浙江省金华市东阳六校2023-2024学年九年级第一学期数学期中试卷
试卷更新日期：2023-12-20 类型：期中考试
一、选择题（本题有10小题，每小题3分，共30分）
-
1. 抛物线y＝3x2+2开口方向是（ ）A、向上 B、向下 C、向左 D、向右2. 下列成语或词语所反映的事件中，属于随机事件的是（ ）A、瓜熟蒂落 B、旭日东升 C、缘木求鱼 D、守株待兔3. 剪纸是我国民间艺术，入选“人类非物质文化遗产”，如图剪纸图案是一个中心对称图形，将其绕中心旋转一定角度后，依然与原图形重合，这个角度不可以是（ ）
A、60° B、90° C、120° D、180°4. 已知 ， 则的值是（ ）A、3 B、-3 C、 D、-5. 如图是2022年杭州亚运会徽标的示意图，若AO＝5，BO＝2，∠AOD＝120°，则阴影部分面积为（ ）
A、14π B、2π C、 D、7π6. 如图，四边形ABCD内接于⊙O ， 已知点C为的中点，若∠A＝50°，则∠CBD的度数为（ ）
A、50° B、40° C、30° D、25°7. 表格列出的是一个二次函数的自变量x与函数y的几组对应值：其中，a的值为（ ）x
…
-5
-4
-3
-2
-1
0
…
y
…
4
0
-2
-2
0
a
…
A、4 B、3 C、2 D、18. 如图，⊙O的半径是2，直线l与⊙O相交于A、B两点，M、N是⊙O上的两个动点，且在直线l的异侧，若∠AMB=45°，则四边形MANB面积的最大值是（ ）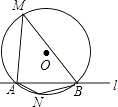
A、2 B、4 C、4 D、89. 大自然是美的设计师，即使是一片小小的树叶，也蕴含着“黄金分割”，如图，P为AB的黄金分割点（AP＞PB），则下列结论中正确的是（ ）
A、AB2＝AP2+BP2 B、BP2＝AP•BA C、 D、10. 已知抛物线y＝-x2+bx+3的顶点坐标为（1，4），若关于x的一元二次方程-x2+bx+3-t＝0（t为实数）在-1≤x≤5范围内有两个不同的实数根，则实数t的取值范围是（ ）A、-12≤t＜4 B、t＜4 C、-12＜t≤0 D、0≤t＜4二、填空题（本题共6小题，每小题4分，共24分）
-
11. 已知⊙O的半径为6cm ， 线段OP的长为4cm ， 则点P在⊙O（填“内”、“外”、“上”）．12. 在一个不透明的袋子里装有红球、黄球共20个，这些球除颜色外其他都相同．小明通过多次重复试验发现，摸出红球的频率稳定在0.4左右，则袋子中红球的个数最有可能是个。13. 如图，直线y＝x-1与抛物线y＝x2-3x+2都经过点A（1，0）和B（3，2），则不等式x-1≥x2-3x+2的解集是 ．
14. 如图，在边长为的正方形网格中，、、、为格点，连接、相交于点 ， 则的长为.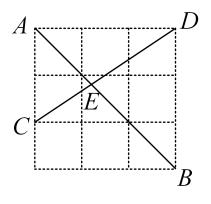
15. 如图，一个扇形纸片的圆心角为90°，半径为6，将这张扇形纸片折叠，使点A与点O恰好重合，折痕为CD，则阴影部分的面积为.
16. 图1是一个瓷碗，图2是其截面图，碗体DEC呈抛物线状（碗体厚度不计），碗口宽CD＝12cm ， 此时面汤最大深度EG＝8cm ．
(1)、当面汤的深度ET为4cm时，汤面的直径PQ长为；(2)、如图3，把瓷碗绕点B缓缓倾斜倒出部分面汤，当∠ABM＝45°时停止，此时碗中液面宽度CH＝ ．三、 解答题（共题共8小题，共66分，各小题都必须写出解答过程）
-
17. 有一张明星演唱会的门票，小明和小亮都想获得这张门票，亲自体验明星演唱会的热烈气氛，小红为他们出了一个主意，方法就是：从印有1、2、3、4、5、4、6、7的8张扑克牌中任取一张，抽到比4大的牌，小明去；否则，小亮去．(1)、求小明抽到4的概率；(2)、你认为这种方法对小明和小亮公平吗？请说明理由；18. 已知线段a、b、c满足 ，且a+2b+c＝26.(1)、求a、b、c的值；(2)、若线段x是线段a、b的比例中项，求x.19. 如图，在平面直角坐标系中，△ABC的三个顶点坐标分别为A（-1，3），B（-3，0），C（-1，0），把△ABC绕点C按顺时针方向旋转90°后得到△A1B1C ． （每个方格的边长均为1个单位）
(1)、画出△A1B1C并直接写出：A1的坐标为 ， B1的坐标为 ；(2)、判断直线AB与直线A1B1的位置关系为 ．20. 如图，AB是⊙O的直径，点C ， D是⊙O上的点，且OD∥BC ， AC分别与BD ． OD相交于点E ， F ．
(1)、求证：点D为弧AC的中点；(2)、若DF＝4，AC＝16，求⊙O的直径．21. 如图，一位同学通过调整自己的位置，设法使三角板的斜边保持水平，并且边DE与点B在同一直线上，已知两条边DE＝0.4m ， EF＝0.2m ， 测得边DF离地面AC＝1.5m ， CD＝8m ， 求树高．
22. 足球训练中球员从球门正前方8米的A处射门，球射向球门的路线呈抛物线．当球飞行的水平距离为6米时，球达到最高点，此时球离地面3米．现以O为原点建立如图所示直角坐标系．
(1)、求抛物线的函数表达式；(2)、已知球门高OB为2.44米，通过计算判断球能否射进球门（忽略其他因素）；(3)、已知点C为OB上一点，OC＝2.25米，若射门路线的形状、最大高度均保持不变，当时球员带球向正后方移动n米再射门，足球恰好经过OC区域（含点O和C），求n的取值范围．23.【模型呈现：材料阅读】
如图1，点B ， C ， E在同一直线上，点A ， D在直线CE的同侧，△ABC和△CDE均为等边三角形，AE ， BD交于点F ， 对于上述问题，存在结论（不用证明）：
⑴△BCD≌△ACE ．
⑵△ACE可以看作是由△BCD绕点C旋转而成．
(1)、【模型改编：问题解决]点A ， D在直线CE的同侧，AB＝AC ， ED＝EC ， ∠BAC＝∠DEC＝50°，直线AE ， BD交于F ， 如图1：点B在直线CE上，
①求证：△BCD∽△ACE ．
②求∠AFB的度数．
③如图2：将△ABC绕点C顺时针旋转一定角度．
补全图形，则∠AFB的度数为 ▲ ．
④若将“∠BAC＝∠DEC＝50°”改为“∠BAC＝∠DEC＝m°”，则∠AFB的度数为 ▲ ． （直接写结论）
(2)、【模型拓广：问题延伸】如图3：在矩形ABCD和矩形DEFG中，AB＝2，AD＝ED＝2 ， DG＝6，连接AG ， BF ， 求的值．
24. 已知，直角△ABC中，∠BAC＝90°，BC＝10，AB＝6，过A，B两点作圆交射线CA于点D ， 交射线CB于点E。
(1)、如图1，当点D在线段AC中点时，求BD的长。(2)、如图2，当点D在线段AC上时，若点D为中点，求BD的长。(3)、如图3，连接AE，若△AEC为等腰三角形，求所有满足条件的BD的值。