浙江省金华市金华四中2023-2024学年九年级第一学期数学期中试卷
试卷更新日期：2023-12-20 类型：期中考试
一、选择题（本大题有10小题，每小题3分，共30分.请选出各题中一个符合题意的正确选项.不选、多选、错选均不给分）
-
1. 一个数的相反数是5，则这个数是（ ）．A、 B、±5 C、-5 D、52. 下列计算，结果等于a4的是（ ）．A、(a2)2 B、a5-a C、a+3a D、a8÷a23. 已知三角形三边长分别为2，3，x ， 若x为奇数，则x的值为（ ）．A、1 B、3 C、5 D、74. 如图所示的是某地12月28日的天气预报，图中关于温度的信息是（ ）．
A、下降19℃ B、下降10℃ C、最低零下10℃ D、最低零下19℃5. “概率”的英文单词是“Probability”，如果在组成该单词的所有字母中任意取出一个字母，则取到字母“b”的概率是（ ）A、 B、 C、 D、16. 北京大兴国际机场采用“三纵一横”全向型跑道构型，如图，侧向跑道AB在点O南偏东70°的方向上，则这条跑道所在射线OB与正北方向所成角的度数为（ ）．
A、160° B、110° C、70° D、20°7. 把一元二次方程x2-4x+1=0配方得（ ）．A、(x-2)2=3 B、(x-2)2=-3 C、(x+2)2=3 D、(x+2)2=-38. 如图，以O为圆心，半径为1的弧交坐标轴于A ， B两点，M是上一点不与A ， B重合 ， 连接OM ， 设∠MOB=α，则点M的坐标为（ ）．
A、(sinα ， cosα) B、(cosα ， sinα) C、(cosα ， cosα) D、(sinα ， sinα)9. 如图，从一块半径为20cm的圆形铁皮上剪出一个圆心角是60°的扇形ABC ， 则此扇形围成的圆锥的侧面积为（ ）．
A、50πcm2 B、100πcm2 C、100πcm2 D、200πcm210. 勾股定理是人类最伟大的科学发现之一，在我国古算书《周髀算经》中早有记载．如图1，以直角三角形的各边为边分别向外作正方形，再将较小的两个正方形分别绕直角三角形斜边上的两顶点旋转得到图2．则图2中阴影部分面积等于（ ）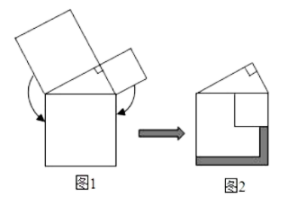
A、直角三角形的面积 B、最大正方形的面积 C、最大正方形与直角三角形的面积和 D、较小两个正方形重叠部分的面积二、填空题（本大题共6小题，共24分）
-
11. 请写出一个比π大的无理数 ．12. 某同学连续五次考试的数学成绩分别是93、79、85、95、90，则这组数据的中位数是 ．13. 如果a+b＝10，ab＝19，则a2b+ab2的值为 ．14. 如图，一个长方体木箱沿斜面下滑，当木箱滑至如图位置时，AB=3m，已知木箱高BE=m，斜坡角为30°，则木箱端点E距地面AC的高度EF为
15. 已知二次函数y＝x2﹣2x+2在t≤x≤t+1时的最小值是t，则t的值为.16. 如图是一种手机三脚架，它通过改变锁扣C在主轴AB上的位置调节三脚架的高度，其它支架长度固定不变，已知支脚DE=AB ． 底座CD⊥AB ， BG⊥AB ， 且CD=BG ， F是DE上的固定点，且EF：DF=2：3．
(1)、当点B ， G ， E三点在同一直线上（如图1所示）时，测得tan∠BED=2；设BC=5a ， 则FG=(用含a的代数式表示)；(2)、在(1)的条件下，若将点C向下移动24cm，则点B ， G ， F三点在同一直线上（如图2），此时点A离地面的高度是cm．三、解答题（本大题共8小题，共66分）
-
17. 计算：(－2)－1－4sin60°++()0 ．18. 解方程： ．19. 一个三位正整数，将它的个位数字与百位数字交换位置，所得的新数恰好与原数相同，我们把这样的三位正整数称为“对称数”，如555，323，191都是“对称数”．(1)、请你写出2个“对称数”；(2)、嘉琪说：“任意一个“对称数”减去其各位数字之和，所得的结果都是9的倍数．”他的说法是否正确，请说明理由．20. 某市旅游景区有A、B、C、D、E等著名景点，该市旅游部门统计绘制出今年“五•一”长假期间旅游情况统计图，根据以下信息解答下列问题：
(1)、今年“五•一”期间，该市周边景点共接待游客多少万人？扇形统计图中A景点所对应的圆心角的度数是多少？并补全条形统计图．(2)、根据近几年到该市旅游人数增长趋势，预计明年“五•一”节将有80万游客选择该市旅游，请估计有多少万人会选择去E景点旅游？21. 已知，AB为⊙O的直径，PA ， PC是⊙O的的切线，切点分别为A ， C ， 过点C作CD∥AB交⊙O于D ．
(1)、如图1，当P ， D ， O共线时，若半径为r ， 求证：CD=r；(2)、如图2，当P ， D ， O不共线时，若DE=2，CE=8，求tan∠POA ．22. 已知平面直角坐标系中，直线AB与反比例函数y=（x＞0）的图象交于点A（1，3）和点B（3，n），与x轴交于点C ， 与y轴交于点D ．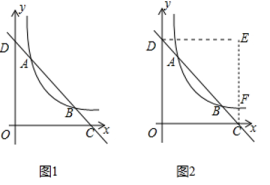
(1)、求反比例函数的表达式及n的值；(2)、将△OCD沿直线AB翻折，点O落在第一象限内的点E处，EC与反比例函数的图象交于点F ．①请求出点F的坐标；
②将线段BF绕点B旋转，在旋转过程中，求线段OF的最大值．
23. 某数学兴趣小组对函数y＝|x2+2x|的图象和性质进行了探究，探究过程如下所示，其中自变量x取全体实数，x与y的几组对应值如表所示．x
-4
-3
-2
-1
0
1
2
3
y
8
m
0
n
0
3
8
15
(1)、根据如表数据填空：m＝ ， n＝；(2)、在如图所示的平面直角坐标系中描点，并用平滑的曲线将函数图象补充完整；
(3)、观察该函数的图象，解决下列问题．①该函数图象与直线y＝的交点有 个；
②当x取何值时，y随x的增大而减小，请写出x的取值范围；
③在同一平面内，若直线y＝x+b与函数y＝|x2+2x|的图象有a个交点，且a≥3，求b的取值范围．
24. 如图1，矩形ABCD中，AB=a ， BC=6，点E ， F分别为AD ， AB边上任意一点，现将△AEF沿直线EF对折，点A对应点为点P ．
(1)、若点B与点F重合①如图2，若a=5，当点P落在BC中垂线上时，求AE的长；
②当点P可以两次落在在BC中垂线上时，求a取值范围；
(2)、如图3，连接BD ， 若a=4，AE=2AF ， 直线FP交△BCD的边于点G ， 是否存在点G ， 使得以E ， G ， P为顶点的三角形与△AEF相似．若存在，请求出AE的长；若不存在，请说明理由．