湖北省武汉市新洲区邾城街2023-2024学年八年级上学期数学期中试卷

试卷更新日期：2023-12-20 类型：期中考试

进入出卷网下载

一、选择题。（本大题共10小题，每小题3分，共30分，在每小题的4个选项中只有一个选项是符合题目要求的）

1. 2023年9月，第19届亚运会在杭州举行，这是继1990年北京亚运会、2010年广州亚运会之后，中国第三次举办亚洲最高规格的国际综合性体育赛事．如图所示的是此届亚运会中所出现的部分体育图标，其中轴对称图形有几个？（）

A、0个 B、1个 C、2个 D、3个

查看试题解析
2. 修理一把摇晃的椅子，我们可以斜着钉上一块木条（如图），其中所涉及的数学原理是（）

A、两边之和大于第三边 B、三角形稳定性 C、两点之间线段最短 D、两点确定一条直线

查看试题解析
3. 根据下列已知条件，能画出唯一△ABC的是（）

A、∠A＝60°，∠B＝45°，AB＝4 B、AB＝5，BC＝3，AC＝8 C、∠C＝90°，AB＝6 D、AB＝4，BC＝3，∠A＝30°

查看试题解析
4. 如图，在 $△ A B C$ 中，分别以 $A$ ， $C$ 为圆心，大于 $\frac{1}{2} A C$ 长为半径作弧，两弧分别相交于 $M$ ， $N$ 两点，作直线 $M N$ ，分别交线段 $B C$ ， $A C$ 于点 $D$ ， $E$ ．若 $A E = 2 c m$ ， $△ A B C$ 的周长为 $15 c m$ ，则 $△ A B D$ 的周长为（）

A、 $11 c m$ B、 $13 c m$ C、 $15 c m$ D、 $17 c m$

查看试题解析
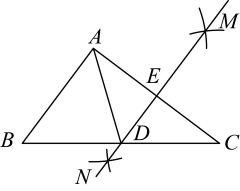5. 在学习“认识三角形”一节时，小颖用四根长度分别为2cm ， 3cm ， 4cm ， 5cm的小棒摆三角形，那么所摆成的三角形的周长不可能是（）

A、9cm B、10cm C、11cm D、12cm

查看试题解析
6. 一个多边形的外角和等于它的内角和的 $\frac{1}{2}$ 倍，那么这个多边形从一个顶点引对角线的条数是（）条．

A、3 B、4 C、5 D、6

查看试题解析
7. 如图，BD是△ABC的中线，点E、F分别为BD、CE的中点，若△AEF的面积为4cm² ，则△ABC的面积是（）

A、12cm² B、16cm² C、20cm² D、24cm²

查看试题解析
8. 已知一张三角形纸片ABC（如图甲），其中AB＝AC ．将纸片沿过点B的直线折叠，使点C落到AB边上的E点处，折痕为BD（如图乙）．再将纸片沿过点E的直线折叠，点A恰好与点D重合，折痕为EF（如图丙）．原三角形纸片ABC中，∠ABC的大小为（）

A、60° B、72° C、36° D、90°

查看试题解析
9. 如图，∠A+∠B+∠C+∠D+∠E+∠F为（）

A、180° B、360° C、540° D、720°

查看试题解析
10. 如图，在△ABC中，∠ABC＝45°，CD⊥AB于点D ， BE平分∠ABC ，且BE⊥AC于点E ，与CD相交于点F ， H是BC边的中点，连接DH与BE相交于G ，下列结论：①BF＝AC；②AE＝ $\frac{1}{2}$ BF；③∠A＝67.5°；④S_四边形_ADGE＝S_四边形_GHCE；⑤△DGF是等腰三角形．其中正确的有（）

A、5个 B、2个 C、4个 D、3个

查看试题解析

二、填空题。（本大题共6小题每小题3分共18分）

11. 某汽车的标志图案是一个轴对称图形．在如图所示的直角坐标系中，y轴是其对称轴．若点A的坐标是（-3，4），则点C的坐标为．

查看试题解析
12. 三角形的两边长分别为3、4，且周长为奇数，这样的三角形共有个．

查看试题解析
13. 如图，在平面直角坐标系中，根据尺规作图的痕迹在第二象限内作出点P（m-1，2n），则m与n的数量关系是．

查看试题解析
14. 如图，△ABC内部有一点E ，点E到△ABC三个顶点的距离相等，△ABC外部有一点O ，点O到三角形三条边的距离相等，连接BE ， CE ， BO ， CO ，若∠BOC＝50°，∠BEC的度数是．

查看试题解析
15. 在△ABC中，AB＝AC ，其中一个内角度数是40°，点D在直线BC边上，连接AD ，若△ABD为直角三角形，则∠ADC的度数为．

查看试题解析
16. 如图， $△ A B C$ 与 $△ A E F$ 中，AB=AE ， BC=EF ， ∠B=∠E ， AB交EF于D ．给出下列结论：①∠AFC=∠C；②DF=CF；③FA是∠DFC的平分线；④∠BFD=∠CAF ．其中正确的结论是：（填写所有正确结论的序号）．

查看试题解析

三、解答题。（本大题共8小题共72分）

17. 如图是雨伞在开合过程中某时刻的截面图，伞骨 $A B = A C$ ， $D$ ， $E$ 分别是 $A B$ ， $A C$ 的中点， $D M$ ， $E M$ 是连接弹簧 $M$ 和伞骨的支架，且 $D M = E M$ ，在弹簧向上滑动的过程中，试说明 $A M$ 平分 $∠ B A C$ ．

查看试题解析
18. 如图，已知∠1＝∠2，CD⊥AB于点D ， BE⊥AC于点E ， BE ， CD交于点O ，求证：OC＝OB ．

查看试题解析
19. 如图，在△ABC中，BD平分∠ABC ， CD平分∠ACB ， DE⊥AB于点E ．

(1)、若∠A＝70°，∠ABC＝60°，求∠BDC的度数；

(2)、若DE＝4，BC＝9，求△BCD的面积．

查看试题解析
20. 小明准备用一段长30m的篱笆围成一个三角形场地用来饲养家兔，已知第一条边长为am ，由于受地势限制，第二条边长只能是第一条边长的2倍多2m ．

(1)、第三条边长为m（用含a的式子表示）；

(2)、如果围成的三角形是等腰三角形，请求出a的值．

查看试题解析
21. 如图在由正方形组成的7×8网格中，每个小正方形的顶点叫做格点，点A ， B ， C都是格点，仅用无刻度直尺，在给定的网格中完成画图．

(1)、在图（1）中，另画出△MNC ，使△MNC≌△ABC（M为A的对应点）；

(2)、在图（1）中，画出△ABC的中线CD；

(3)、在图（2）中，画出△ABC的高BE；再在高BE上画点F ，使得∠AFE＝45°．

查看试题解析
22.

(1)、【初步探索】
如图1：在四边形ABCD中，AB＝AD ， ∠B＝∠ADC＝90°，E、F分别是BC、CD上的点，且EF＝BE+FD ，探究图中∠BAE、∠FAD、∠EAF之间的数量关系．
小王同学探究此问题的方法是：延长FD到点G ，使DG＝BE ．连接AG ，先证明△ABE≌△ADG ，再证明△AEF≌△AGF ，可得出结论，他的结论应是；

(2)、【灵活运用】
如图2，若在四边形ABCD中，AB＝AD ， ∠B+∠D＝180°．E、F分别是BC、CD上的点，且EF＝BE+FD ，上述结论是否仍然成立，并说明理由；

(3)、【拓展延伸】
如图3，已知在四边形ABCD中，∠ABC+∠ADC＝180°，AB＝AD ，若点E在CB的延长线上，点F在CD的延长线上，如图3所示，仍然满足EF＝BE+FD ，请写出∠EAF与∠DAB的数量关系，并给出证明过程．

查看试题解析
23.

(1)、【问题情境】如图1，A，B两点分别位于一个池塘的两端，小明想用绳子测量A，B间的距离，但绳子不够长，一个叔叔帮他出了这样一个主意：先在地上取一个可以直接到达A点和B点的点C，连接 $A C$ 并延长到D，使 $C D = C A$ ；连接 $B C$ 并延长到E，使 $C E = C B$ ，连接 $D E$ 并测量出它的长度，如果 $D E = 100$ 米，那么 $A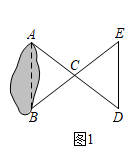 B$ 间的距离为米．

(2)、【探索应用】如图2，在 $△ A B C$ 中，若 $A B = 5 ， A C = 3$ ，求 $B C$ 边上的中线 $A D$ 的取值范围．
解决此问题可以用如下方法：延长 $A D$ 到点E使 $D E = A D$ ，再连接 $B E$ （或将 $△ A C D$ 绕着点D逆时针旋转 $180 °$ 得到 $△ E B D$ ），把 $A B 、 A C ， 2 A D$ 集中在 $△ A B E$ 中，利用三角形三边的关系即可判断，中线 $A D$ 的取值范围是；

(3)、【拓展提升】如图3，在 $△ A B C$ 中， $∠ A C B = 90 ° ， A B = A D ， A C = A E ， ∠ B A D = ∠ C A E = 90 ° ， C A$ 的延长线交 $D E$ 于点F，求证： $D F = E F$ ．

查看试题解析
24. 如图，在平面直角坐标系中，△AOB为等腰直角三角形，A（4，4）

(1)、求B点坐标；

(2)、若C为x轴正半轴上一动点，以AC为直角边作等腰直角△ACD ， ∠ACD＝90°，连OD ，求∠AOD的度数；

(3)、过点A作y轴的垂线交y轴于E ， F为x轴负半轴上一点，G在EF的延长线上，以EG为直角边作等腰Rt△EGH ，过A作x轴垂线交EH于点M ，连FM ，等式 $\frac{A M - F M}{O F}$ ＝1是否成立？若成立，请证明：若不成立，说明理由．

查看试题解析