湖北省随州市曾都区、随县2023-2024学年九年级上学期数学5校联考11月月考试卷

试卷更新日期：2023-12-20 类型：期中考试

进入出卷网下载

一、选择题（每小题3分，共30分）

1. 下列图形是我国国产品牌汽车的标识，在这些汽车标识中，是中心对称图形的是（　　）

A、 B、 C、 D、

查看试题解析
2. $x = 1$ 是关于x的一元二次方程 $x^{2} + a x + 3 b = 0$ 的解，则 $2 a + 6 b =$ （）

A、 $- 2$ B、 $- 3$ C、 $- 1$ D、 $- 6$

查看试题解析
3. 已知二次函数 $y = - 3 {(x - 2)}^{2} - 3$ ，下列说法正确的是（）

A、对称轴为 $x = - 2$ B、顶点坐标为 $(2 ， 3)$ C、函数的最大值是 $- 3$ D、函数的最小值是 $- 3$

查看试题解析
4. 如图，正五边形 $A B C D E$ 内接于 $⊙ O$ ，连接 $O C ， O D$ ，则 $∠ B A E - ∠ C O D =$ （）

A、 $60 °$ B、 $54 °$ C、 $48 °$ D、 $36 °$

查看试题解析
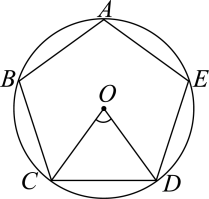5. 如图，在 $△ A B C$ 中， $∠ B A C = 120 °$ ，将 $△ A B C$ 绕点C逆时针旋转得到 $△ D E C$ ，点A ， B的对应点分别为D ， E ，连接AD.当点A ， D ， E在同一条直线上时，下列结论不一定正确的是（）

A、 $∠ B C E = 60 °$ B、 $A B ∥ C D$ C、 $∠ A C B = ∠ B C D$ D、 $A B + A C = A E$

查看试题解析
6. 据国家统计局发布的《2022年国民经济和社会发展统计公报》显示，2020年和2022年全国居民人均可支配收入分别为3.2万元和3.7万元．设2020年至2022年全国居民人均可支配收入的年平均增长率为x，依题意可列方程为（）

A、 $3.2 (1 - x)^{2} = 3.7$ B、 $3.2 (1 + x)^{2} = 3.7$ C、 $3.7 (1 - x)^{2} = 3.2$ D、 $3.7 (1 + x)^{2} = 3.2$

查看试题解析
7. 我国古代数学名著《九章算术》中有这样一道题：“今有圆材，径二尺五寸．欲为方版，令厚七寸，问广几何？”结合右图，其大意是：今有圆形材质，直径 $B D$ 为25寸，要做成方形板材，使其厚度 $C D$ 达到7寸．则 $B C$ 的长是（）

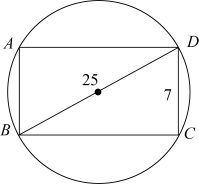A、 $\sqrt{674}$ 寸 B、25寸 C、24寸 D、7寸

查看试题解析
8. 如图，在 $⊙ O$ 的内接四边形ABCD中，AB是直径， $∠ B C D = 120 °$ ，过D点的切线PD与直线AB交于点P ，则 $∠ A D P$ 的度数为（）

A、30° B、35° C、40° D、45°

查看试题解析
9. 图（1）是一个横断面为抛物线形状的拱桥，当水面在l时，拱顶（拱桥洞的最高点）离水面2m，水面宽为4m.如果水面宽度为6m，则水面下降（）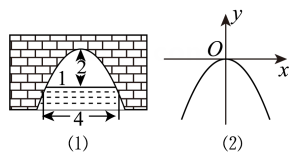

A、2m B、2.5m C、3m D、3.5m

查看试题解析
10. 将进货单价为50元的某种商品按零售价每个60元出售时，每周能卖出100个，若这种商品零售价每涨价1元，周销售量就减少2个，但物价部门规定，最高售价不能高于成本价的30％，则每周获得的最大利润为（）.

A、80元 B、1000元 C、1750元 D、1800元

查看试题解析

二、填空题（每小题3分，共18分）

11. 当方程 $(m - 1) x^{m^{2} + 1} - (m + 1) x - 2 = 0$ 是一元二次方程时，m的值为.

查看试题解析
12. 已知圆锥的母线长13cm，高是12cm，则这个圆锥的侧面积组成的阴影部分的面积是 $c^{2}$ .

查看试题解析
13. 如图，在平面直角坐标系 $x O y$ 中， $A B ⊥ x$ 轴于点B ，将 $△ A B O$ 绕点B逆时针旋转60°得到 $△ C B D$ .若点A的坐标为 $(2 ， 2 \sqrt{3})$ ，则点C的坐标为.

查看试题解析
14. 如图， $△ A B C$ 的内切圆 $⊙ O$ 与AB、AC、BC、分别相切于点D、E、F ，且 $A B = 5$ ， $B C = 13$ ， $C A = 12$ ，则图中由线段AD、AE及 $\overset{⌢}{D E}$ 组成的阴影部分的面积是.

查看试题解析
15. 抛物线 $y = a x^{2} + b x + c$ 的对称轴是直线 $x = - 1$ ，且过点 $(1 ， 0)$ .顶点位于第二象限，其部分图像如图所示，给出以下判断：① $a b < 0$ ；② $4 a - 2 b + c > 0$ ；③ $3 a + c > 0$ ；④抛物线上有两点 $P (x_{1} ， y_{1})$ 和 $Q (x_{2} ， y_{2})$ ，若 $x_{1} < - 1 < x_{2}$ ，且 $x_{1} + x_{2} > - 2$ ，则 $y_{1} < y_{2}$ ；⑤直线 $y = x + 1$ 与抛物线 $y = a x^{2} + b x + c$ 两个交点的横坐标分别为 $x_{1}$ ， $x_{2}$ ，则 $x_{1} + x_{2} + x_{1} x_{2} = - 5$ .其中正确的就（填写序号）.

查看试题解析
16. 如图，在矩形ABCD中， $A B = 2$ ， $A D = 3$ ，动点P在矩形的边上沿 $B \to C \to D \to A$ 运动。当点P不与点A、B重合时，将 $△ A B P$ 沿AP对折，得到 $△ A B^{'} P$ ，连接 $C B^{'}$ ，则在点P的运动过程中，线段 $C B^{'}$ 的最小值为.

查看试题解析

三、解答题（共72分）

17. 解方程：

(1)、 $2 x^{2} + 3 x - 1 = 0$

(2)、 $2 (x + 3) = x^{2} - 9$

查看试题解析
18. 把抛物线 $1 ： = 2 + 2 + 3$ 先向右平移4个单位长度，再向下平移5个单位长度得到抛物线2.

(1)、直接写出抛物线2的函数关系式；

(2)、点 $P (a ， - 6)$ 能否在拋物线2上？请说明理由；

查看试题解析
19. 已知关于x的一元二次方程 $x^{2} - 2 (a - 1) x + a^{2} - 2 = 0$ 有两个不相等的实数根 $x_{1}$ ， $x_{2}$ .

(1)、求a的取值范围；

(2)、若 $x_{1}$ ， $x_{2}$ 满足 $x_{1}^{2} + x_{2}^{2} - x_{1} x_{2} = 19$ ，求a的值.

查看试题解析
20. 如图，AB为 $⊙ O$ 的直径，AC是弦，点D是 $\overset{⌢}{B C}$ 的中点， $D E ⊥ A C$ ，交AC的延长线于点E.

(1)、判断直线DE与 $⊙ O$ 的位置关系，并说明理由；

(2)、若 $D E = 4$ ， $⊙ O$ 的半径为5，求CE的长.

查看试题解析
21.

(1)、如图1，在平面直角坐标系中， $△ A B C$ 的三个顶点都在格点上，点A的坐标为 $(2 ， 4)$ ，画出 $△ A B C$ 关于原点O成中心对称的 $△ A^{'} B^{'} C^{'}$ ，并写出点C的对应点 $C^{'}$ 的坐标    ▲    ；

(2)、如图2，是由小正方形组成的 $6 \times 6$ 的网格，点A ， B ， C均在格点上.
①点M在线段AB右侧的格点上，点A绕点M顺时针旋转 $α$ 度 $(0 < α < 180)$ 可与点B重合，则 $α =$         ；点A转过的路径长为        ；
②在图中确定 $△ A B C$ 的外心（仅用无刻度的直尺在给定的网格中完成画图，画图过程用虚线表示）.

查看试题解析
22. 一次足球训练中，小明从球门正前方20m的A处射门，球射向球门的路线呈抛物线.当球飞行的水平距离为15m时，球达到最高点，此时球离地面3m.已知球门高OB为2.44m，现以O为原点建立如图所示直角坐标系.

(1)、求抛物线的函数表达式，并通过计算判断球能否射进球门（忽略其他因素）.

(2)、对本次训练进行分析，若射门路线的形状、最大高度均保持不变，则当时他应该带球向正后方移动多少米射门，才能让足球经过点O正上方2.25m处？

查看试题解析
23. 如图①，在等腰直角三角形ABC中， $∠ B A C = 90 °$ ， D ， E分别为AB ， AC的中点，F为线段DE上一动点（不与D ， E重合），将线段AF绕点A按逆时针方向旋转90°得到AG ，连接BF ， CG.

(1)、求证： $△ A B F ≌ △ A C G$ .

(2)、如图②，连接EG ， FG ， FG交AC于点H.
①证明：在点F的运动过程中，总有∠ $F E G = 90 °$ ；
②若 $A B = A C = 2 \sqrt{2}$ ，直接写出当DF的长度是多少时，为 $△ A G H$ 为等腰三角形？

查看试题解析
24. 如图所示，抛物线与x轴交于A、B两点，与y轴交于点C ，且 $O A = 1$ ， $O B = O C = 4$ .

(1)、求抛物线的解析式；

(2)、若连接AC、BC.动点D从点A出发，在线段AB上以每秒1个单位长度向点B做匀速运动；同时，动点E从点B出发，在线段BC上以每秒个单位长度向点C做匀速运动，当其中一点到达终点时，另一点随之停止运动，连接DE ，设运动时间为t秒.在D、E运动的过程中，当t为何值时，四边形ADEC的面积最小，最小值为多少？

(3)、点M是抛物线上位于x轴上方的一点，点N在x轴上，是否存在以点M为直角顶点的等腰直角三角形CMN？若存在，求出点M的坐标，若不存在，请说明理由.

查看试题解析