湖北省十堰市张湾区、郧阳区2023-2024学年八年级上学期数学期中试卷
试卷更新日期：2023-12-20 类型：期中考试
一、选择题（本题有10个小题，每小题3分，共30分）
-
1. 如图图案中不是轴对称图形的是（ ）A、
B、
C、
D、
2. 下列长度的三根线段，能构成三角形的是（ ）A、3cm ， 10cm ， 5cm B、4cm ， 8cm ， 4cm C、5cm ， 13cm ， 12cm D、2cm ， 7cm ， 4cm3. 如果一个多边形的内角和是它外角和的3倍，那么这个多边形的边数为（ ）A、6 B、8 C、9 D、104.如图，△ABC中，BO，CO分别是∠ABC，∠ACB的平分线，∠A=50°，则∠BOC等于（ ）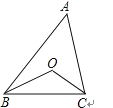
A、110° B、115° C、120° D、130°5. 如图，在△ABC和△DEC中，已知CB＝CE ， 还需添加两个条件才能使△ABC≌△DEC ， 不能添加的一组条件是（ ）
A、AC＝DC ， AB＝DE B、∠ACD＝∠BCE ， ∠B＝∠E C、AB＝DE ， ∠B＝∠E D、AC＝DC ， ∠A＝∠D6. 如图所示，△ABC与△ADE顶点A重合，点D，E分别在边BC，AC上，且AB＝AC，AD＝DE，∠B＝∠ADE＝40°，则∠EDC的度数为（ ）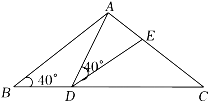
A、20° B、30° C、40° D、507. 如图，在△ABC中，分别以点A和点C为圆心，大于AC的长为半径画弧交于两点，过这两点作直线交AC于点E ， 交BC于点D ， 连接AD ， 若△ADB的周长为15，AE＝4，则△ABC的周长为（ ）
A、23 B、21 C、19 D、178. 如图，在Rt△ABC中，∠ACB＝90°，∠CAB＝36°，以C为原点，AC所在直线为y轴，BC所在直线为x轴建立平面直角坐标系，在坐标轴上取一点M使△MAB为等腰三角形，符合条件的M点有（ ）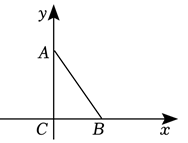
A、5个 B、6个 C、7个 D、8个9. 如图所示，在△ABC中，AB＝8，点M是BC的中点，AD是∠BAC的平分线，作MF∥AD交AC于F ， 已知CF＝10，则AC的长为（ ）
A、12 B、11 C、10 D、910. 如图，在△OAB和△OCD中，OA＝OB ， OC＝OD ， OA＞OC ， ∠AOB＝∠COD＝30°，如图，连接AC ， BD交于点M ， AC与OD相交于E ， BD与OA相交于F ， 连接OM ． 则下列结论中：①AC＝BD；②∠AMB＝30°；③△OEM≌△OFM；④MO平分∠BMC ． 正确的个数有（ ）
A、1个 B、2个 C、3个 D、4个二、填空题（每题3分，共18分．请直接将答案填写在答题卡中，不写过程）
-
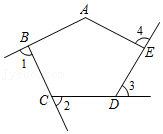
11. 一个等腰三角形的两边长分别是4和9，则周长是 ．12. 如图，五边形ABCDE中，∠A＝125°，则∠1+∠2+∠3+∠4的度数是 ．
13. 如图，已知 ABD≌ ACE，∠A＝53°，∠B＝21°，则∠BEC＝°.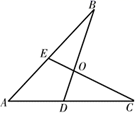
14. 点P（a ， 3）与点P'（2，b）关于x轴对称，则a-b的值为 ．15. 如图，在△ABC中，∠ACB=90°，∠B =30°，CD是高．若AD=2，则BD= ．
16. 如图，点P是∠AOB内一点，点P关于OA的对称点为C ， 点P关于OB的对称点为D ， 连结CD交OA、OB于点M和点N ， 连结PM、PN ． 若∠AOB＝70°，则∠MPN的大小为度．
三、解答题（本题有9个小题，共72分）
-
17. 如图，点B ， E ， C ， F在同一条直线上，AB∥DE ， AB＝DE ， BE＝CF ， 求证：AC＝DF ．
18. 如图， ， ， ， 求的度数.
19. 如图所示，在平面直角坐标系中，已知A（0，1），B（2，0），C（4，3）．
(1)、在平面直角坐标系中画出△ABC ， 并求出△ABC的面积；(2)、在（1）的条件下，把△ABC先关于y轴对称得到△A'B'C'，再向下平移3个单位得到△A″B″C″，直接写出△A″B″C″的坐标；20. 小明在计算一个多边形的内角和时，因粗心多加了一个外角，计算出的结果是1506°，请你求出这是一个几边形？并且至少有一个内角是多少度？21. 如图，在△ABC和△BDE中，点C在边BD上，边AC交边BE于点F ， 若AC＝BD ， AB＝ED ， BC＝BE ． 求证：∠AFB＝2∠ACB ．
22. 如图，在△ABC中，BD是AC边上的高，∠A＝70°，CE平分∠ACB交BD于点E ， ∠BEC＝118°，求∠ABC ．
23. 如图：点E、F在BC上， ， ， ，AF与DE交于点G.过点G作 ，垂足为H.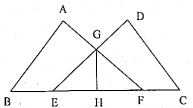
(1)、求证：(2)、求证：24. 如图，△ABC中，∠ACB＝90°，AC＝BC ， BD平分∠ABC ， AE⊥BD ， 垂足为E ．
(1)、求∠EAC的度数；(2)、若AE＝2，求BD的长．25. 如图，在平面直角坐标系中，点A的坐标为（-4，0），点B的坐标为（4，0），点C的坐标为（0，4），△EDC是以点D为直角顶点的等腰直角三角形，点E在第三象限，点D在x轴上运动．
(1)、如图1所示，当点D的坐标为（1，0）时，求点E的坐标；(2)、如图2所示，点D在线段OB上运动时，连接AC、BC ， 连接AE并延长与y轴交于点P ， 求点P的坐标；(3)、如图3，设△EDC的边ED与y轴交于点G ， CE与x轴交于点F ， 当点D在线段OB上运动，且满足时，在线段DE上取点H ， 且DH＝EG ， 连接HF交y轴于点Q ． 下列结论：①CG＝2FH；②△QGH为等腰三角形，其中只有一个结论是正确，请判断出正确的结论，并写出证明过程．