湖北省十堰市张湾区、郧阳区2023-2024学年九年级上学期数学期中试卷

试卷更新日期：2023-12-20 类型：期中考试

进入出卷网下载

一、选择题（本题有10个小题，每小题3分，共30分）

1. 下列图形是我国国产品牌汽车的标识，在这些汽车标识中，是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 将一元二次方程3x²+1＝6x化成一般形式后，二次项系数和一次项系数分别是（）

A、3，1 B、3，6 C、-3，-6 D、3，-6

查看试题解析
3. 二次函数y＝（x+2）²-3的顶点坐标是（）

A、（2，-3） B、（2，3） C、（-2，-3） D、（-2，3）

查看试题解析
4. 下列方程有两个相等的实数根的是（）

A、x²﹣2x+1＝0 B、x²﹣3x+2＝0 C、x²﹣2x+3＝0 D、x²﹣9＝0

查看试题解析
5. 在平面直角坐标系中，点A（-4，3）关于原点的对称点的坐标为（）

A、（4，3） B、（-3，4） C、（-4，-3） D、（4，-3）

查看试题解析
6. 将抛物线y＝-2（x-1）²+3向左平移3个单位，再向上平移2个单位，得到的抛物线是（）

A、y＝-2（x-4）²-1 B、y＝-2（x+2）²+5 C、y＝-2（x+2）²+1 D、y＝-2（x-4）²+5

查看试题解析
7. 如图， $△ A B C$ 中， $∠ A C B = 90^{°} ， ∠ A B C = 40^{°}$ ．将 $△ A B C$ 绕点B逆时针旋转得到 $△ A^{'} B C^{'}$ ，使点C的对应点 $C^{'}$ 恰好落在边 $A B$ 上，则 $∠ {CAA}^{'}$ 的度数是（）

A、 $50^{°}$ B、 $70^{°}$ C、 $110^{°}$ D、 $120^{°}$

查看试题解析
8. 某种防疫物资原价为50元/件，经过连续两次降价后售价为28元/件，每次降价的百分率均为x ，根据题意所列方程正确的是（）

A、50（1-x）²＝50-28 B、50（1-x）²＝28 C、50（1-2x）＝28 D、50（1-x²）＝28

查看试题解析
9. 如图，点A、B、C、D、P都在⊙O上，OC⊥AB ．若∠ADC＝α（0°＜α＜90°），则∠APB＝（）

A、90°+α B、180°-α C、180°-2α D、2α

查看试题解析
10. 如图，已知二次函数y＝ax²+bx+c（a、b、c为常数，且a≠0）的图象顶点为P（1，m），经过点A（2，1）．有以下结论：①a＜0；②abc＞0；③4a+2b+c＝1；④x＞1时，y随x的增大而减小；⑤对于任意实数t ，总有at²+bt≤a+b ，其中正确的有（）

A、2个 B、3个 C、4个 D、5个

查看试题解析

二、填空题。（每题3分，共18分）

11. 抛物线y＝3（x-1）²+8的顶点坐标为．

查看试题解析
12. 若m、n是一元二次方程x²+3x-9＝0的两个根，则m²+4m+n的值是．

查看试题解析
13. 如图，在△OAB绕点O逆时针旋转70°得到△OCD ，若∠A＝100°，∠D＝50°，则∠AOD的度数是．

查看试题解析
14. 如图，AB是⊙O的直径，若AC＝2，∠D＝60°，则BC长等于．

查看试题解析
15. 对于实数p、q ，我们用符号min{p ， q}表示p、q两数中较小的数，如min{1，2}＝1，若min{（x﹣1）² ， x²}＝1，则x＝．

查看试题解析
16. 在等边△ABC中，D是边AC上一点，连接BD ，将△BCD绕点B逆时针旋转60°，得到△BAE ，连接ED ，若BC＝5，BD＝4，则以下四个结论中：①△BDE是等边三角形；②AE∥BC；③△ADE的周长是9；④∠ADE＝∠BDC ．其中正确的序号是．（请填写序号）

查看试题解析

三、解答题。（共72分）

17. 解下列方程：

(1)、2x²＋6x＋3＝0

(2)、(x＋2)²＝3(x＋2)

查看试题解析
18. 如图，在平面直角坐标系中，△ABO的顶点均在格点上．

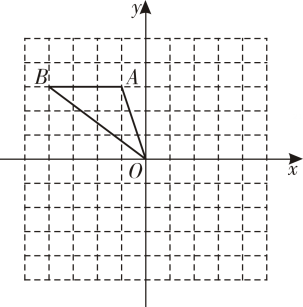(1)、画出△ABO关于原点O对称的图形△A₁B₁O；

(2)、画出△ABO绕原点O顺时针旋转90°后得到的图形△A₂B₂O ，并写出点B的对应点B₂的坐标．

查看试题解析
19. 如图，一圆弧形桥拱的圆心为 $E$ ，拱桥的水面跨度 $A B = 80$ 米，桥拱到水面的最大高度 $D F$ 为 $20$ 米.求：

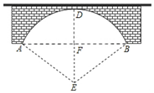(1)、桥拱的半径；

(2)、现水面上涨后水面跨度为 $60$ 米，求水面上涨的高度为米.

查看试题解析
20. 已知关于x的方程x²-4x+k+1＝0有两个实数根．

(1)、求k的取值范围；

(2)、若△ABC的一条边BC的长为 $\sqrt{10}$ ，另两边AB ， AC的长分别为关于x的一元二次方程x²-4x+k+1＝0的两个实数根．当k＝2时，请判断△ABC的形状，并说明理由；

(3)、设方程两实数根分别为x₁、x₂ ，且 $\frac{3}{x_{1}} + \frac{3}{x_{2}}$ ＝x₁x₂-4，求实数k的值．

查看试题解析
21. 改善小区环境，争创文明家园.如图所示，某社区决定在一块长（ $A D$ ）16 $m$ ，宽（ $A B$ ）9 $m$ 的矩形场地 $A B C D$ 上修建三条同样宽的小路，其中两条与 $A B$ 平行，另一条与 $A D$ 平行，其余部分种草.要使草坪部分的总面积为112 $m^{2}$ ，则小路的宽应为多少？

查看试题解析
22. 如图，AB是⊙O的直径，C、D为⊙O上的点，且BC∥OD ，过点D作DE⊥AB于点E ．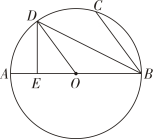

(1)、求证：BD平分∠ABC；

(2)、若BC＝3，DE＝2，求⊙O的半径长．

查看试题解析
23. 某公司电商平台，在2023年国庆长假期间，举行了商品打折促销活动，经市场调查发现，某种商品的周销售量y（件）是关于售价x（元/件）（x为正整数）的一次函数，如表仅列出了该商品的售价x ，周销售量y ，周销售利润W（元）的三组对应值数据．
x
40
70
90
y
180
90
30
W
3600
4500
2100

(1)、该商品进价（元/件），y关于x的函数解析式是（不要求写出自变量的取值范围）；

(2)、在销售过程中要求售价不低于进价，售价x为多少时，周销售利润W最大，并求出此时的最大利润；

(3)、因该商品原料涨价，进价提高了m（元/件）（m＞0的整数），该商品在今后的销售中，公司发现当售价为63元/件时，周销售利润最大，请直接写出m的值．

查看试题解析
24.

(1)、如图1，已知，正方形ABCD和正方形CEFG ，点G在CD边上，点E在BC边上，则BE与DG的数量关系为；

(2)、将（1）中的正方形CEFG绕点C旋转至图2时，（1）中的结论是否成立？若成立，请给以证明；若不成立，请说明理由；

(3)、若AB＝5 $\sqrt{2}$ ， CE= $\sqrt{2}$ ，将（1）中正方形CEFG绕点C旋转α度（0＜α＜90），如图3，当B ， E ， G三点在一条直线上时，求DG的长．

查看试题解析
25. 如图①，抛物线y＝ax²+ $\frac{16}{9}$ x+c ，与x轴交于A ， B两点（A在B的左边），与y轴交于C点，顶点为E ，其中，点A坐标为（-1，0），对称轴为x＝2．

(1)、求此抛物线解析式；

(2)、在第四象限的抛物线上找一点F ，使S_△_FBC＝S_△_ACB ，求点F的坐标；

(3)、如图②，点P是x轴上一点，点E与点H关于点P成中心对称，点B与点Q关于点P成中心对称，当以点Q ， H ， E为顶点三角形是直角三角形时，求P的坐标．

查看试题解析

x	40	70	90
y	180	90	30
W	3600	4500	2100