湖北省黄石市大冶市2023-2024学年八年级上学期数学期中试卷(人教版)
试卷更新日期:2023-12-20 类型:期中考试
一、选择题(3分×10=30分)
-
1. 在以下绿色食品、回收、节能、节水四个标志中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列各组线段中,能构成三角形的是( )A、2,5,8 B、3,3,6 C、3,4,5 D、4,5,93. 如图,AB=AC , D , E分别是AB , AC上的点,下列条件不能判断△ABE≌△ACD的是( )
2. 下列各组线段中,能构成三角形的是( )A、2,5,8 B、3,3,6 C、3,4,5 D、4,5,93. 如图,AB=AC , D , E分别是AB , AC上的点,下列条件不能判断△ABE≌△ACD的是( ) A、∠B=∠C B、BE=CD C、AD=AE D、BD=CE4. 在下列条件:①;②;③;④中,能确定为直角三角形的条件有( )A、2个 B、3个 C、4个 D、5个5. 如图, , 是的中线, , 则的面积为( )
A、∠B=∠C B、BE=CD C、AD=AE D、BD=CE4. 在下列条件:①;②;③;④中,能确定为直角三角形的条件有( )A、2个 B、3个 C、4个 D、5个5. 如图, , 是的中线, , 则的面积为( ) A、112 B、102 C、122 D、2246. 如图,为等边三角形,延长CB到D , 使 . 延长BC到点E , 使 . 连接AD , AE , 则的度数是( )
A、112 B、102 C、122 D、2246. 如图,为等边三角形,延长CB到D , 使 . 延长BC到点E , 使 . 连接AD , AE , 则的度数是( ) A、 B、 C、 D、7. 如图,在折纸活动中,小明制作了一张△ABC纸片,D,E分别是边AB,AC上的点,将△ABC沿着DE折叠压平,点A与点A′重合,若∠A=70°,则∠1+∠2的度数为( )
A、 B、 C、 D、7. 如图,在折纸活动中,小明制作了一张△ABC纸片,D,E分别是边AB,AC上的点,将△ABC沿着DE折叠压平,点A与点A′重合,若∠A=70°,则∠1+∠2的度数为( ) A、110° B、140° C、220° D、70°8. 如图,在等腰中, , AB的垂直平分线DE交AB于点D , 交AC于点E , BC的垂直平分线PQ交BC于点P , 交AC于点Q , 连接BE , BQ , 则( )
A、110° B、140° C、220° D、70°8. 如图,在等腰中, , AB的垂直平分线DE交AB于点D , 交AC于点E , BC的垂直平分线PQ交BC于点P , 交AC于点Q , 连接BE , BQ , 则( ) A、62° B、58° C、52° D、46°9. 如图,点D是等边△ABC的边AC上一点,以BD为边作等边△BDE,点C,E在BD同侧,下列结论:①∠ABD=30°;②CE∥AB;③CB平分∠ACE;④CE=AD,其中错误的有( )
A、62° B、58° C、52° D、46°9. 如图,点D是等边△ABC的边AC上一点,以BD为边作等边△BDE,点C,E在BD同侧,下列结论:①∠ABD=30°;②CE∥AB;③CB平分∠ACE;④CE=AD,其中错误的有( ) A、0个 B、1个 C、2个 D、3个10. 已知 , 在内有一定点P , 点M , N分别是上的动点,若的周长最小值为3,则的长为( )
A、0个 B、1个 C、2个 D、3个10. 已知 , 在内有一定点P , 点M , N分别是上的动点,若的周长最小值为3,则的长为( ) A、1.5 B、3 C、2 D、2.5
A、1.5 B、3 C、2 D、2.5二、填空题(3分×6=18分)
-
11. 点关于轴对称的点的坐标为 .12. 三角形两边长分别是2,4,第三边长为偶数,第三边长为 .13. 一个多边形的每一个内角都是 , 这是一个边形.14. 如图, , , 若 , 则PD的长为 .
 15. 如图,在等腰Rt△ABC中,∠ACB=90°,点D为Rt△ABC内一点,∠ADC=90°,若△BCD的面积为8,则CD= .
15. 如图,在等腰Rt△ABC中,∠ACB=90°,点D为Rt△ABC内一点,∠ADC=90°,若△BCD的面积为8,则CD= . 16. 如图,在四边形中,对角线平分 , , 则 .
16. 如图,在四边形中,对角线平分 , , 则 .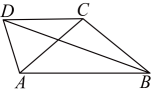
三、解答题(共8小题,8分+8分+8分+8分+9分+9分+10分+12分)
-
17. 如图,点B , E , C , F在一条直线上, . 求证: .
 18. 如图,在中,于点D , 平分 .
18. 如图,在中,于点D , 平分 . (1)、若 , 求的度数;(2)、若 , , 求的度数(用含、的式子来表示).19. 如图,BD , CE是△ABC的高,BD , CE相交于点F , BE=CD .
(1)、若 , 求的度数;(2)、若 , , 求的度数(用含、的式子来表示).19. 如图,BD , CE是△ABC的高,BD , CE相交于点F , BE=CD .
求证:
(1)、Rt△BCERt△CBD;(2)、AF平分∠BAC .20. 如图,在中,边的垂直平分线分别交边于点E , F , 过点A作于点D , 且D为线段的中点.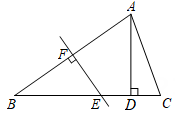 (1)、求证:;(2)、若 , 求的度数.21. 如图,四边形中, , E为的中点,连接并延长交的延长线于点F .
(1)、求证:;(2)、若 , 求的度数.21. 如图,四边形中, , E为的中点,连接并延长交的延长线于点F . (1)、求证:;(2)、连接 , 若 .
(1)、求证:;(2)、连接 , 若 .①求证:是的角平分线;
②若时,求的长.
22. 如图,在的正方形网格中,点A、B、C都在格点上点D是与网格线的交点且 , 仅用无刻度的直尺在给定网格中完成画图,画图过程用虚线表示.
⑴作边上高 .
⑵画出点D关于的对称点F;
⑶画射线 , 平分 .
23. 已知,在等边三角形中,点E在上,点D在的延长线上,且 . (1)、【特殊情况,探索结论】如图1,当点E为的中点时,确定线段与的大小关系,请你直接写出结论: (填“>”、“<”或“=”).(2)、【特例启发,解答题目】如图2,当点E为边上任意一点时,确定线段与的大小关系,请你写出结论,并说明理由. ▲ (填“>”、“<”或“=”);理由如下,过点E作 , 交于点F . (请你完成以下解答过程).(3)、【拓展结论,设计新题】在等边三角形中,点E在直线上,点D在线段的延长线上,且 , 若的边长为1, , 求的长(直接写出结果).24. 如图1,在平面直角坐标系中,直线AB分别交y轴、x轴于点 , 点 , 且a、b满足 .
(1)、【特殊情况,探索结论】如图1,当点E为的中点时,确定线段与的大小关系,请你直接写出结论: (填“>”、“<”或“=”).(2)、【特例启发,解答题目】如图2,当点E为边上任意一点时,确定线段与的大小关系,请你写出结论,并说明理由. ▲ (填“>”、“<”或“=”);理由如下,过点E作 , 交于点F . (请你完成以下解答过程).(3)、【拓展结论,设计新题】在等边三角形中,点E在直线上,点D在线段的延长线上,且 , 若的边长为1, , 求的长(直接写出结果).24. 如图1,在平面直角坐标系中,直线AB分别交y轴、x轴于点 , 点 , 且a、b满足 . (1)、求a , b的值:(2)、以AB为边作 , 点C在直线AB的右侧且 , 求点C的坐标;(3)、若(2)的点C在第四象限(如图2),AC与x交于点D , BC与y轴交于点E , 连接DE , 过点C作交x于点F .
(1)、求a , b的值:(2)、以AB为边作 , 点C在直线AB的右侧且 , 求点C的坐标;(3)、若(2)的点C在第四象限(如图2),AC与x交于点D , BC与y轴交于点E , 连接DE , 过点C作交x于点F .
①求证;
②直接写出点C到DE的距离.