湖北省恩施土家族苗族自治州巴东县2023-2024学年九年级上学期数学期中试卷
试卷更新日期:2023-12-20 类型:期中考试
一、选择题(每小题3分,共计36分)
-
1. 下列图形中,属于中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 将一元二次方程化成一般形式,则它的一次项系数是( )A、4 B、6 C、8 D、253. 二次函数的图象大致是( )A、
2. 将一元二次方程化成一般形式,则它的一次项系数是( )A、4 B、6 C、8 D、253. 二次函数的图象大致是( )A、 B、
B、 C、
C、 D、
D、 4. 在平面直角坐标系中,点关于原点的对称点为 , 则的值为( )A、 B、8 C、6 D、5. 如图,正方形ABCD和的周长之和为a(a为常数)cm,设圆的半径为xcm,正方形的边长为ycm,阴影部分的面积为 , 当x在一定范围内变化时,y和S都随x的变化而变化,则y与x , S与x满足的函数关系分别是( )
4. 在平面直角坐标系中,点关于原点的对称点为 , 则的值为( )A、 B、8 C、6 D、5. 如图,正方形ABCD和的周长之和为a(a为常数)cm,设圆的半径为xcm,正方形的边长为ycm,阴影部分的面积为 , 当x在一定范围内变化时,y和S都随x的变化而变化,则y与x , S与x满足的函数关系分别是( ) A、二次函数关系,二次函数关系 B、二次函数关系,一次函数关系 C、一次函数关系,一次函数关系 D、一次函数关系,二次函数关系6. 若二次函数有最大值,则“□”中可填的数是( )A、2 B、1 C、0 D、7. 若关于x的一元二次方程有两个实数根,则k的取值范围是( )A、 B、 C、且 D、且8. 将含有角的直角三角板按如图所示的方式放置在平面直角坐标系中,OB在x轴上,将三角板绕原点O顺时针旋转,当点B恰好落在y轴的负半轴上时停止.若 , 则点A的对应点的坐标是( )
A、二次函数关系,二次函数关系 B、二次函数关系,一次函数关系 C、一次函数关系,一次函数关系 D、一次函数关系,二次函数关系6. 若二次函数有最大值,则“□”中可填的数是( )A、2 B、1 C、0 D、7. 若关于x的一元二次方程有两个实数根,则k的取值范围是( )A、 B、 C、且 D、且8. 将含有角的直角三角板按如图所示的方式放置在平面直角坐标系中,OB在x轴上,将三角板绕原点O顺时针旋转,当点B恰好落在y轴的负半轴上时停止.若 , 则点A的对应点的坐标是( ) A、 B、 C、 D、9. 将一元二次方程化成的形式,则( )A、1 B、 C、2023 D、10. 我国古代数学家研究过一元二次方程的正数解的几何解法.以方程 , 即为例说明,《方图注》中记载的方法是:构造如图所示正方形,其中大正方形的面积是 , 同时它又等于四个矩形的面积加上中间小正方形的面积,即 , 因此 . 小明用此方法解关于x的方程时,构造出同样的图形,已知大正方形的面积为14,小正方形的面积为4,则( )
A、 B、 C、 D、9. 将一元二次方程化成的形式,则( )A、1 B、 C、2023 D、10. 我国古代数学家研究过一元二次方程的正数解的几何解法.以方程 , 即为例说明,《方图注》中记载的方法是:构造如图所示正方形,其中大正方形的面积是 , 同时它又等于四个矩形的面积加上中间小正方形的面积,即 , 因此 . 小明用此方法解关于x的方程时,构造出同样的图形,已知大正方形的面积为14,小正方形的面积为4,则( ) A、 , B、 , C、 , D、 ,11. 如图,在方格纸中,将 绕点 按顺时针方向旋转90°后得到 ,则下列四个图形中正确的是( )
A、 , B、 , C、 , D、 ,11. 如图,在方格纸中,将 绕点 按顺时针方向旋转90°后得到 ,则下列四个图形中正确的是( )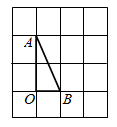 A、
A、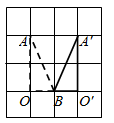 B、
B、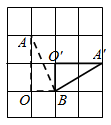 C、
C、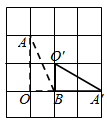 D、
D、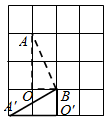 12. 如图,已知二次函数的图象与x轴交于A , B两点,与y轴交于点C , 对称轴为直线 . 直线与抛物线交于C , D两点,D点在x轴下方且横坐标小于3,则下列结论:
12. 如图,已知二次函数的图象与x轴交于A , B两点,与y轴交于点C , 对称轴为直线 . 直线与抛物线交于C , D两点,D点在x轴下方且横坐标小于3,则下列结论:
①;
②;
③;
④ .
其中正确的有( )
A、4个 B、3个 C、2个 D、1个二、填空题(每小题3分,共计12分)
-
13. 如果2是一元二次方程的一个根,则 , 它的另一个根是 .14. 将抛物线先向右平移3个单位,再向上平移4个单位,得到的抛物线是 .15. 张师傅去年开了一家超市,今年2月份开始盈利,3月份盈利5000元,5月份盈利达到7200元,从3月到5月,每月盈利的平均增长率都相同,则每月盈利的平均增长率是 .16. 如图,为等边三角形, , 于点D , 点E为线段AD上的动点,连接CE , 以CE为边在下方作等边 , 连接DF , 则线段DF的最小值为 .

三、解答题(共计72分)
-
17. 如图二次函数的图象与x轴交于点 , , 与y轴交于点C , 请回答下列问题:
 (1)、方程的根是;(2)、若方程有两个不相等的实数根,则m的取值范围是;(3)、若直线BC的解析式为 , 则的解集为;(4)、当y有最大值时,x的取值范围是 .18. 解方程: .
(1)、方程的根是;(2)、若方程有两个不相等的实数根,则m的取值范围是;(3)、若直线BC的解析式为 , 则的解集为;(4)、当y有最大值时,x的取值范围是 .18. 解方程: .解:设 , 则原方程变为: , 解得, , .
当时, , 解得 , ;
当时, , 解得 , ;
∴原方程的解为: , , , .
上面解方程的方法简称换元法.
请利用上述方法,解方程:
(1)、;(2)、 .19. 用18m长的篱笆(虚线部分)围成两面靠墙的矩形苗圃.其中一面墙长8m,另一面墙的使用不受限制. (1)、设矩形的长BE为xm,矩形的面积为 , 求y与x的函数关系式;(2)、x为何值时,矩形的面积最大?最大面积是多少?20. 已知,在矩形ABCD中,点E是线段AB上的一个动点,将线段DE绕点D逆时针旋转得到DF , 过F作于点G , 连接EF , 取EF的中点H , 连接DH , AH .
(1)、设矩形的长BE为xm,矩形的面积为 , 求y与x的函数关系式;(2)、x为何值时,矩形的面积最大?最大面积是多少?20. 已知,在矩形ABCD中,点E是线段AB上的一个动点,将线段DE绕点D逆时针旋转得到DF , 过F作于点G , 连接EF , 取EF的中点H , 连接DH , AH . (1)、证明:;(2)、当点H与点G重合时,探究线段AH与DE的关系.21. 已知关于x的一元二次方程有实数根.(1)、求实数k的取值范围;(2)、设方程的两个实数根分别为 , , 若 . 求k的值.22. 如图1,O为正方形ABCD对角线的交点,点E , F在正方形边BC , CD上, , 连接OE , OF , EF .
(1)、证明:;(2)、当点H与点G重合时,探究线段AH与DE的关系.21. 已知关于x的一元二次方程有实数根.(1)、求实数k的取值范围;(2)、设方程的两个实数根分别为 , , 若 . 求k的值.22. 如图1,O为正方形ABCD对角线的交点,点E , F在正方形边BC , CD上, , 连接OE , OF , EF . (1)、求证:;(2)、如图2,若M为CD的中点,N为BC的中点,MN与EF交于点K , 请探究点K是否平分EF , 说明理由.23. 2023年8月5日,在成都举行的第31届世界大学生夏季运动会女子篮球金牌赛中,中国队以99比91战胜日本队,夺得冠军.女篮最重要的球员之一韩旭在日常训练中也迎难而上,勇往直前.投篮时篮球以一定速度斜向上抛出,不计空气阻力,在空中划过的运动路线可以看作是抛物线的一部分.建立平面直角坐标系xOy , 篮球从出手到进入篮筐的过程中,它的竖直高度y(单位:m)与水平距离x(单位:m)近似满足二次函数关系,篮筐中心距离地面的竖直高度是3m,韩旭进行了两次投篮训练.(1)、第一次训练时,韩旭投出的篮球的水平距离x与竖直高度y的几组数据如下:
(1)、求证:;(2)、如图2,若M为CD的中点,N为BC的中点,MN与EF交于点K , 请探究点K是否平分EF , 说明理由.23. 2023年8月5日,在成都举行的第31届世界大学生夏季运动会女子篮球金牌赛中,中国队以99比91战胜日本队,夺得冠军.女篮最重要的球员之一韩旭在日常训练中也迎难而上,勇往直前.投篮时篮球以一定速度斜向上抛出,不计空气阻力,在空中划过的运动路线可以看作是抛物线的一部分.建立平面直角坐标系xOy , 篮球从出手到进入篮筐的过程中,它的竖直高度y(单位:m)与水平距离x(单位:m)近似满足二次函数关系,篮筐中心距离地面的竖直高度是3m,韩旭进行了两次投篮训练.(1)、第一次训练时,韩旭投出的篮球的水平距离x与竖直高度y的几组数据如下:水平距离x/m
0
1
2
3
4
竖直高度y/m
2.0
3.0
3.6
3.8
3.6
①在平面直角坐标系xOy中,描出上表中各对对应值为坐标的点,并用平滑的曲线连接;

②结合表中数据和所画图象,直接写出篮球运行的最高点距离地面的竖直高度是 m,并求y与x满足的函数解析式;
③已知此时韩旭距篮筐中心的水平距离5m,韩旭第一次投篮练习是否成功,请说明理由;
(2)、第二次训练时,韩旭出手时篮球的竖直高度与第一次训练相同,此时投出的篮球的竖直高度y与水平距离x近似满足函数关系 , 若投篮成功,此时韩旭距篮筐中心的水平距离d5(填“>”,“=”或“<”).24. 如图,已知抛物线与y轴交于点 , 与x轴交于点 , B两点,P为抛物线上的动点.已知点 . (1)、直接写出抛物线的解析式;(2)、能否成为等边三角形,请说明理由;(3)、若 , 求点P的坐标.
(1)、直接写出抛物线的解析式;(2)、能否成为等边三角形,请说明理由;(3)、若 , 求点P的坐标.