(人教版)2023-2024学年九年级上学期数学 25.2 用列举法求概率 期末复习(吉林地区专用)
试卷更新日期:2023-12-20 类型:复习试卷
一、选择题
-
1. 某地区共有甲、乙、丙、丁四个足球队,现从这四个队中随机抽取两个队进行一场足球比赛则恰好抽到甲队和丁队的概率是( )A、 B、 C、 D、2. 将分别标有“孔”、“孟”、“乏”、“乡”汉字的四个小球装在一个不透明的口集中,这些球除汉字外无其他差别,每次摸球前先搅拌均匀.随机摸出一球,不放回;再随机摸出一球.两次摸出的球上的汉字能组成“孔孟”的概率是( )A、 B、 C、 D、3. 现有三张正面分别标有数字 , , 的不透明卡片,它们除数字外其余完全相同,将它们背而面朝上洗均匀,随机抽取一张,记下数字后放回,背面朝上洗均匀,再随机抽取一张记下数字,前后两次抽取的数字分别记为m,n,则点 在第二象限的概率为( )A、 B、 C、 D、4. 从1,2,3,6中任意选两个数,记作a和b,那么点(a,b)在函数y=图象上的概率是( )A、 B、 C、 D、5. 一枚质地均匀的正方体骰子的六个面上分别刻有1到6的点数,投掷此骰子,朝上面的点数为奇数的概率是( )A、 B、 C、 D、6. 如图的两个圆盘中均有5个数字,同时旋转两个圆盘,指针落在某一个数上的机会均等,那么两个指针同时落在奇数上的概率是( )
 A、 B、 C、 D、7. 在两个不透明的口袋中分别装有三个颜色分别为红色、白色、绿色的小球,这三个小球除颜色外其余都相同,若分别从两个口袋中随机取出一个小球,则取出的两个小球颜色相同的概率为( )A、 B、 C、 D、8. 物理某一实验的电路图如图所示,其中K1 , K2 , K3 为电路开关,L1 , L2为能正常发光的灯泡.任意闭合开关K1 , K2 , K3中的两个,那么能让两盏灯泡同时发光的概率为( )
A、 B、 C、 D、7. 在两个不透明的口袋中分别装有三个颜色分别为红色、白色、绿色的小球,这三个小球除颜色外其余都相同,若分别从两个口袋中随机取出一个小球,则取出的两个小球颜色相同的概率为( )A、 B、 C、 D、8. 物理某一实验的电路图如图所示,其中K1 , K2 , K3 为电路开关,L1 , L2为能正常发光的灯泡.任意闭合开关K1 , K2 , K3中的两个,那么能让两盏灯泡同时发光的概率为( )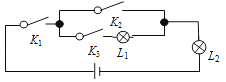 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 小明的壁橱里有四只袜子,两只白色的,两只黑色的小明没往框里看,随意拿出来两只袜子,两只袜子颜色相同的概率为10. 大数据分析技术为打赢疫情防控阻击战发挥了重要作用.如图是小明同学的吉祥码示意图,用黑白打印机打印在边长为2cm的正方形区域内,图中黑色部分的总面积为2.4cm2 , 现在向正方形区域内随机掷点,点落入黑色部分的概率为 .
 11. 如图,一个可以自由转动的转盘被等分成8个扇形区域,并涂上了相应的颜色,转动转盘,转盘停止后,指针指向黄色区域的概率是 .
11. 如图,一个可以自由转动的转盘被等分成8个扇形区域,并涂上了相应的颜色,转动转盘,转盘停止后,指针指向黄色区域的概率是 . 12. 有三张大小、形状完全相同的卡片.卡片上分别写有数字4、5、6,搅匀后从这三张卡片中同时抽取两张,则抽取的两张卡片上数字之和为奇数的概率是 .13. 某游戏的规则为:选手蒙眼在一张如图所示的正方形黑白格子纸(九个小正方形面积相等)上描一个点,若所描的点落在黑色区域,获得笔记本一个;若落在白色区域,获得钢笔一支.选手获得笔记本的概率为
12. 有三张大小、形状完全相同的卡片.卡片上分别写有数字4、5、6,搅匀后从这三张卡片中同时抽取两张,则抽取的两张卡片上数字之和为奇数的概率是 .13. 某游戏的规则为:选手蒙眼在一张如图所示的正方形黑白格子纸(九个小正方形面积相等)上描一个点,若所描的点落在黑色区域,获得笔记本一个;若落在白色区域,获得钢笔一支.选手获得笔记本的概率为 14. 如图,有甲,乙两个可以自由转动的转盘,若同时转动,则停止后指针都落在阴影区域内的概率是
14. 如图,有甲,乙两个可以自由转动的转盘,若同时转动,则停止后指针都落在阴影区域内的概率是
三、解答题
-
15. 有四张完全一样正面分别写有汉字“吉”、“林”、“七”、“中"的卡片,将其背面朝上并洗匀,从中随机抽取一张,记下卡片正面上的汉字后放回,洗匀后再从中随机抽取一张,请用列表法或者画树状图法求抽取的两张卡片上的汉字相同的概率.16. 两枚质地均匀的正方体骰子,六个面上的点数分别为1,2,3,4,5,6, 同时抛掷这两枚骰子一次,求朝上的面的点数之和为5或9的概率.17. 有两个不透明的口袋,一个口袋装有2个红球、1个白球,另一个口袋装有1个黄球、2个红球,这些球除了颜色外其它完全相同.从两个口袋中各随机摸出1个球,用画树状图(或列表)的方法,求摸出的两个球颜色相同的概率.18. 箱子里有4瓶牛奶,其中有一瓶是过期的.设这四瓶牛奶分别记为A、B、C、D,其中过期牛奶为A.现从这4瓶牛奶中不放回地任意抽取2瓶.(1)、请用树状图或列表法把上述所有等可能的结果表示出来.(2)、抽出的2瓶牛奶中恰好有过期牛奶的概率为19. 箱子里有4瓶牛奶,其中有-瓶是过期的.设这四瓶牛奶分别记为A、B、C、D,其中过期牛奶为A.现从这4瓶牛奶中不放回地任意抽取2瓶.(1)、请用树状图或列表法把上述所有等可能的结果表示出来.(2)、抽出的2瓶牛奶中恰好有过期牛奶的概率为20. 某社区组织 , , , 四个小区的居民进行核酸检测,有很多志愿者参与此项检测工作,志愿者王明和李丽分别被随机安排到这四个小区中的一个小区组织居民排队等候.(1)、王明被安排到小区进行服务的概率是 .(2)、请用列表法或画树状图法求出王明和李丽被安排到同一个小区工作的概率.21. 小华有3张卡片,小明有2张卡片,卡片上的数字如图所示.小华和小明分别从自己的卡片中随机抽取一张.请用画树状图(或列表)的方法,求抽取的两张卡片上的数字和为6的概率.
 22. 有3张不透明的卡片,分别标号为A、B、C,它们除正面上的图案不同外,其他均相同.将这3张卡片背面向上洗匀后放在桌面上.若从中随机抽取1张卡片,记下标号后放回洗匀,再随机抽取1张记下标号,请用画树状图或列表的方法求两次所抽取的卡片恰好都是中心对称图形的概率.
22. 有3张不透明的卡片,分别标号为A、B、C,它们除正面上的图案不同外,其他均相同.将这3张卡片背面向上洗匀后放在桌面上.若从中随机抽取1张卡片,记下标号后放回洗匀,再随机抽取1张记下标号,请用画树状图或列表的方法求两次所抽取的卡片恰好都是中心对称图形的概率.
