（人教版）2023-2024学年九年级上学期数学 24.4 弧长及扇形的面积期末复习(吉林地区专用)

试卷更新日期：2023-12-20 类型：复习试卷

进入出卷网下载

一、选择题

1. 图1是等边三角形铁丝框 $A B C$ ，按图2方式变形成以A为圆心， $A B$ 长为半径的扇形（图形周长保持不变），则所得扇形 $A B C$ 的圆心角的度数是（）

A、 $45 °$ ． B、 $60 °$ ． C、 $\frac{90 °}{π}$ ． D、 $\frac{180 °}{π}$ ．

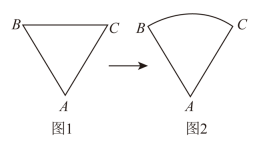查看试题解析
2. 如图，A、B是⊙O上的两点，∠AOB＝120°，OA＝3，则劣弧AB的长是（）

A、π B、2π C、3π D、4π

查看试题解析
3. 如图，圆心重合的两圆半径分别为4、2， $∠ A O B = 120 °$ ，则阴影部分图形的面积为（）

A、4π B、 $\frac{16}{3} π$ C、8π D、16π

查看试题解析
4. 如图，在边长为2的等边 $△ A B C$ 中，按下列步骤作图：①分别以点A和点C为圆心、大于 $A C$ 一半的长为半径作圆弧，两弧相交于点D；②作射线 $B D$ ，与边 $A C$ 相交于点 $E$ ；③以点B为圆心， $B E$ 长为半径作圆弧，交边 $B C$ 于点F.则图中阴影部分（扇形 $B E F$ ）的面积为（）

A、 $\frac{\sqrt{3} π}{6}$ B、 $\frac{π}{4}$ C、 $\frac{π}{3}$ D、 $\frac{2 π}{3}$

查看试题解析
5. 如图，⊙O的半径为6，四边形ABCD内接于⊙O，连接OB、OD，若∠BOD=∠BCD，则 $\overset{⌢}{B D}$ 的长度为（）

A、2π B、 $\frac{3}{2}$ π C、4π D、6π

查看试题解析
6. 如图，直径AB为3的半圆，绕A点逆时针旋转60°，此时点B到了点B′处，则图中阴影部分的面积是（）

A、3π B、 $\frac{3 π}{2}$ C、6π D、24π

查看试题解析
7. 如图，四边形ABCD内接于⊙O．若⊙O的半径为4，∠D=135°，则弧AC的长为（）

A、 $π$ ． B、2 $π$ ． C、4 $π$ ． D、8 $π$ ．

查看试题解析
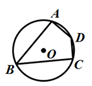8. 如图，⊙A、⊙B、⊙C、⊙D两两外离，且半径都是 $r$ ，则图中的四个扇形（即阴影部分）面积之和是（）

A、 $π r^{2}$ B、 $2 π r^{2}$ C、 $\frac{π r^{2}}{4}$ D、 $\frac{π r^{2}}{2}$

查看试题解析

二、填空题

9. 如图，点C、D是⊙O上直径AB两侧的两点，若∠ACD= 60°．AB=8．则 $\overset{⌢}{B D}$ 的长为（结果保留π）．

查看试题解析
10. 如图，在扇形 $B O C$ 中， $∠ B O C = 60 °$ ， $O D$ 平分 $∠ B O C$ 交 $\overset{�}{B C}$ 于点 $D$ ，点 $E$ 为半径 $O B$ 的中点．若 $O B = 4$ ，则阴影部分的面积为．

查看试题解析
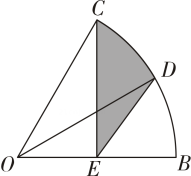11. 如图是由边长为 $1$ 的小正方形组成的 $3 \times 3$ 的网格，每个小正方形的顶点叫做格点 $.$ 点 $A$ 、 $B$ 、 $C$ 、 $D$ 均在格点上，在网格中将点 $B$ 按下列步骤移动：
第一步：点 $B$ 绕点 $A$ 顺时针旋转 $270 °$ 得到点 $B_{1}$ ；
第一步：点 $B_{1}$ 绕点 $C$ 顺时针旋转 $90 °$ 得到点 $B_{2}$ ；
第三步：点 $B_{2}$ 绕点 $D$ 逆时针旋转 $90 °$ 回到点 $B$ ．
则点 $B$ 经过的路径长为．

查看试题解析
12. 如图，在 $R t △ A B C$ 中， $∠ A C B = 90 °$ ， $A C = B C = 2$ ，分别以点 $A$ ， $B$ 为圆心 $.$ 大于 $\frac{1}{2} A B$ 长度为半径画弧，两弧交于点 $P$ ，作射线 $C P$ 交 $A B$ 于点 $D$ ，再以点 $C$ 为圆心， $C D$ 长度为半径画弧，交 $B C$ 于点 $E$ ，则阴影部分的面积为．

查看试题解析
13. 如图，点O是半圆圆心， $B E$ 是半圆的直径，点A、D在半圆上，且 $A D ∥ B O$ ， $∠ A B O = 60 °$ ， $A B = 4$ ，则阴影部分的面积是．

查看试题解析
14. 小张同学准备用矩形纸片做一个圆锥形帽子．如图，在矩形纸片 $A B C D$ 中， $A D = 30 cm ，$ 取 $C D$ 的中点O ，以O为圆心， $30 cm$ 长为半径作弧，分别交 $A D$ 于点E ， $B C$ 于点F ，得到扇形纸片 $E O F$ （阴影部分），发现点E、F分别是边 $A D$ 、 $B C$ 的中点，则此扇形纸片围成圆锥形帽子的底面圆的周长为 $cm$ （结果含 $π$ ）．

查看试题解析

三、解答题

15. 如图， $A B$ 是 $⊙ O$ 的直径， $A D$ 是 $⊙ O$ 的弦，C为 $A B$ 延长线上的点， $∠ D A C = ∠ D C A = 30 °$ ．

(1)、求证： $D C$ 是 $⊙ O$ 的切线．

(2)、若 $⊙ O$ 的半径为6，求 $\overset{⌢}{A D}$ 的长．（结果保留 $π$ ）

查看试题解析
16. 如图，在△ABC中，∠C=90°，∠BAC的平分线交BC于点D，点O在AB上，以点O为圆心，OA为半径的圆恰好经过点D，分别交AC，AB于点E，F．

(1)、试判断直线BC与⊙O的位置关系，并说明理由；

(2)、若BD=2 $\sqrt{3}$ ，BF=2，求阴影部分的面积（结果保留π）．

查看试题解析
17.
如图，已知A（2 $\sqrt{3}$ ， 2）、B（2 $\sqrt{3}$ ， 1），将△AOB绕着点O逆时针旋转，使点A旋转到点A′（﹣2，2 $\sqrt{3}$ ）的位置，B旋转到点B′位置．
（1）求B′点坐标．
（2）求阴影部分面积．

查看试题解析
18.
如图，点A坐标为（﹣2，3），将点A绕原点O顺时针旋转90°得点A′，求A′的坐标．

查看试题解析
19.
如图，点A、B、C、D、E都在⊙O上，AC平分∠BAD，且AB∥CE，求证：AD=CE．

查看试题解析
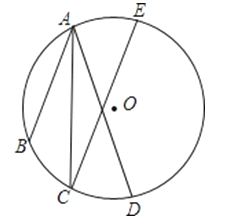20.
如图，AB、CD为⊙O的直径， $\overset{\land}{A C}$ = $\overset{\land}{C E}$ ，求证：BD=CE．

查看试题解析
21.
如图，在⊙O中，C﹑D为⊙O上两点，AB是⊙O的直径，已知∠AOC=130°，AB=2．
求：（1） $\overset{\land}{A c}$ 的长；
（2）∠D的度数．

查看试题解析
22.
）如图，AB是⊙O的直径，弦CD⊥AB，垂足为E，∠CDB=30°，CD=2 $\sqrt{3}$ ，求图中阴影部分的面积．

查看试题解析
23.
如图，秋千拉绳长AB为3米，静止时踩板离地面0.5米，某小朋友荡该秋千时，秋千在最高处时踩板离地面2米（左右对称），请计算该秋千所荡过的圆弧长（精确到0.1米）？

查看试题解析
24.
如图，AB为⊙O的直径，弦AC=2，∠ABC=30°，∠ACB的平分线交⊙O于点D，求：
（1）BC、AD的长；
（2）图中两阴影部分面积的和．

查看试题解析

（人教版）2023-2024学年九年级上学期数学 24.4 弧长及扇形的面积 期末复习(吉林地区专用)

一、选择题

二、填空题

三、解答题

（人教版）2023-2024学年九年级上学期数学 24.4 弧长及扇形的面积期末复习(吉林地区专用)