(人教版)2023-2024学年九年级上学期数学 24.3 正多边形和圆 期末复习(吉林地区专用)
试卷更新日期:2023-12-20 类型:复习试卷
一、选择题
-
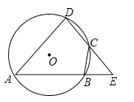
1. 如图,四边形ABCD是圆的内接四边形,∠BAD=108°,E 是BC延长线上一点,若∠ECF=60°,则∠DCF等于( )
 A、30° B、48° C、54° D、60°2. 如图,四边形ABCD是圆内接四边形,∠BAD=108°,E是BC延长线上一点,若∠ECF=60°,则∠DCF的大小是 ( )
A、30° B、48° C、54° D、60°2. 如图,四边形ABCD是圆内接四边形,∠BAD=108°,E是BC延长线上一点,若∠ECF=60°,则∠DCF的大小是 ( )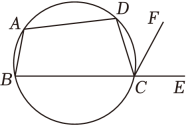 A、30° B、48° C、54° D、60°3. 如图,四边形ABCD是⊙O的内接四边形,若∠B=128°,则∠AOC等于( )
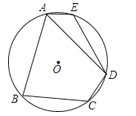
A、30° B、48° C、54° D、60°3. 如图,四边形ABCD是⊙O的内接四边形,若∠B=128°,则∠AOC等于( ) A、100° B、128° C、104° D、124°4. 如图,将透明直尺叠放在正五边形微章ABCDE上,若直尺的下沿MN⊥DE于点O,且经过点B,上沿PQ经过点E,则∠ABM的度数为( )
A、100° B、128° C、104° D、124°4. 如图,将透明直尺叠放在正五边形微章ABCDE上,若直尺的下沿MN⊥DE于点O,且经过点B,上沿PQ经过点E,则∠ABM的度数为( ) A、152° B、126° C、120° D、108°5. 如图,四边形ABCD是圆内接四边形,∠BAD=108°,E是BC延长线上一点,若∠ECF=60°,则∠DCF的大小是( )
A、152° B、126° C、120° D、108°5. 如图,四边形ABCD是圆内接四边形,∠BAD=108°,E是BC延长线上一点,若∠ECF=60°,则∠DCF的大小是( )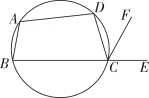 A、30° B、48° C、54° D、60°6. ⊙O的半径为2,则它的内接正六边形的边长为( )A、2 B、2 C、 D、27. 已知直线及直线外一点 , 如图,
A、30° B、48° C、54° D、60°6. ⊙O的半径为2,则它的内接正六边形的边长为( )A、2 B、2 C、 D、27. 已知直线及直线外一点 , 如图,
在直线上取一点 , 以点为圆心,长为半径画半圆,交直线于 , 两点;
连接 , 以点为圆心,长为半径画弧,交半圆于点;
作直线 , 连接 .
根据以上作图过程及所作图形,下列结论中错误的是( ) A、 B、
A、 B、
C、 D、8. 用两种正多边形组合铺满地面,其中的一种是正八边形,则另一种是( )A、正三角形 B、正方形 C、正五边形 D、正六边形二、填空题
-
9. 如图,正五边形ABCDE内接于⊙O,连接AC,则∠BAC的度数是。
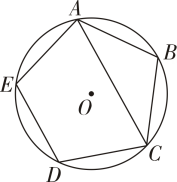 10. 如图是第四套人民币中的菊花1角硬币,则该硬币边缘镌刻的正九边形的一个外角的度数为.
10. 如图是第四套人民币中的菊花1角硬币,则该硬币边缘镌刻的正九边形的一个外角的度数为. 11. 边长相等的正五边形与正六边形按如图所示拼接在一起,则∠ABO的度数为
11. 边长相等的正五边形与正六边形按如图所示拼接在一起,则∠ABO的度数为 12. 将正六边形与正方形按如图所示摆放,且正六边形的边AB与正方形的边CD在一条直线上,则∠BOC的度数是
12. 将正六边形与正方形按如图所示摆放,且正六边形的边AB与正方形的边CD在一条直线上,则∠BOC的度数是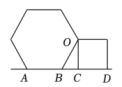 13. 如图,多边形ABCDE为⊙O的内接正五边形,PA与⊙O相切于点A,则∠PAB=
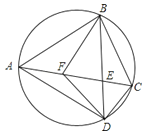
13. 如图,多边形ABCDE为⊙O的内接正五边形,PA与⊙O相切于点A,则∠PAB= 14. 如图,点B , C , D在上,若 , 则的大小是 .
14. 如图,点B , C , D在上,若 , 则的大小是 .
三、解答题
-
15. 如图,圆内接四边形ABCD的对角线AC,BD交于点E,BD平分∠ABC,∠BAC=∠ADB.
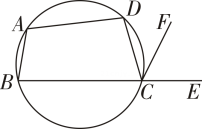
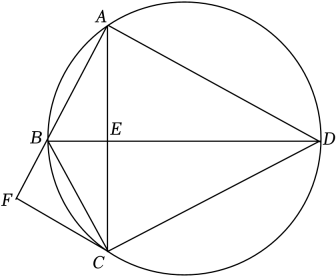 (1)、求证DB平分∠ADC , 并求∠BAD的大小;(2)、过点C作CF∥AD交AB的延长线于点F , 若AC=AD , BF=2求此圆半径的长16. 如图,已知A,B,C,D是⊙O上的四点,延长DC,AB相交于点E.若BC=BE.
(1)、求证DB平分∠ADC , 并求∠BAD的大小;(2)、过点C作CF∥AD交AB的延长线于点F , 若AC=AD , BF=2求此圆半径的长16. 如图,已知A,B,C,D是⊙O上的四点,延长DC,AB相交于点E.若BC=BE.求证:△ADE是等腰三角形.
 17. 如图,已知A、B、C、D是⊙O上的四点,延长DC、AB相交于点E.若BC=BE.求证:△ADE是等腰三角形.
17. 如图,已知A、B、C、D是⊙O上的四点,延长DC、AB相交于点E.若BC=BE.求证:△ADE是等腰三角形.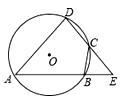 18. 如图,已知等边△ABC内接于⊙O,BD为内接正十二边形的一边,CD=5cm,求⊙O的半径R.
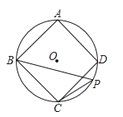
18. 如图,已知等边△ABC内接于⊙O,BD为内接正十二边形的一边,CD=5cm,求⊙O的半径R.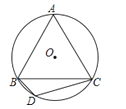 19. 如图,正方形ABCD的外接圆为⊙O,点P在劣弧上(不与C点重合).
19. 如图,正方形ABCD的外接圆为⊙O,点P在劣弧上(不与C点重合).(1)求∠BPC的度数;
(2)若⊙O的半径为8,求正方形ABCD的边长.
 20.
20.如图,已知A、B、C、D是⊙O上的四点,延长DC,AB相交于点E,若DA=DE,求证:△BCE是等腰三角形.
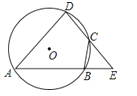 21. 如图,四边形ABCD内接于⊙O,∠ABC=130°,求∠OAC的度数.
21. 如图,四边形ABCD内接于⊙O,∠ABC=130°,求∠OAC的度数.