（人教版）2023-2024学年九年级上学期数学 23.2 中心对称期末复习(吉林地区专用)

试卷更新日期：2023-12-20 类型：复习试卷

进入出卷网下载

一、选择题

1. 下列四幅图片上呈现的是垃圾类型及标识图案，标识图案中是中心对称图形的是（）

A、其它垃圾 B、有害垃圾 C、易腐垃圾 D、可回收物

查看试题解析
2. 下列图形中，不是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 下列图案中，既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
4. 如图，在平面直角坐标系中，点A，C在x轴上，点C的坐标为（-1，0），AC=2，将Rt△ABC先绕点C顺时针旋转90°，再向右平移3个单位长度，则变换后点A的对应点坐标是（）

A、（2，2） B、（1，2） C、（-1，2） D、（2，-1）

查看试题解析
5. 习近平总书记指出：发展新能源汽车是我国从汽车大国走向汽车强国的必由之路．当前随着新一轮科技革命和产业变革孕育兴起，新能源汽车产业正进入加速发展的新阶段，下列图案是我国的一些国产新能源车企的车标，图案既是轴对称图形，又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
6.
对下图的对称性表述，正确的是（）

A、轴对称图形 B、中心对称图形 C、既是轴对称图形又是中心对称图形 D、既不是轴对称图形又不是中心对称图形

查看试题解析
7. 如图，以平行四边形 $A B C D$ 对角线的交点O为原点．平行于 $B C$ 边的直线为x轴，建立如图所示的平面直角坐标系．若D点坐标为 $(5 ， 3)$ ．则B点坐标为（）

A、 $(- 4 ， - 3)$ B、 $(- 3 ， - 5)$ C、 $(- 5 ， - 3)$ D、 $(- 3 ， - 4)$

查看试题解析
8. 如图，在平面直角坐标系中，点A的坐标为 $(0 ， 6)$ ，点B的坐标为 $(3 ， 6)$ ，点C是线段 $A B$ 上的点，将点A绕点C逆时针旋转 $90 °$ 得到点D，若线段 $C D$ 与函数 $y = \frac{5}{x} (x > 0)$ 的图象有交点，则点C的横坐标m的取值范围是（）

A、 $0 \leq m \leq \frac{5}{6}$ B、 $\frac{5}{6} \leq m \leq 1$ C、 $\frac{5}{6} \leq m \leq 2$ D、 $2 \leq m \leq 3$

查看试题解析

二、填空题

9. 如图，在平面直角坐标系中，点 $A$ 的坐标为 $(0 ， 3)$ ，点 $B$ 的坐标为 $(4 ， 0)$ ，连接 $A B$ ，若将 $△ A B O$ 绕点 $B$ 顺时针旋转 $90 °$ ，得到 $△ A' B O'$ ，则点 $A'$ 的坐标为．

查看试题解析
10. 如图，该图形绕其中心旋转能与自身完全重合．则其旋转角最小为度．

查看试题解析
11. 如图， $△ A O B$ 与 $△ C O D$ 关于点 $O$ 成中心对称，已知 $∠ B A O = 90 ° ， A B = 4 ， A O = 3$ ，则 $A D$ 的长为．

查看试题解析
12. 点P（-3，2）关于原点O对称的点P₁的坐标为．

查看试题解析
13. 如图，在平面直角坐标系中，抛物线 $y = a_{1} x^{2} + b_{1} x + c_{1} (a_{1} > 0)$ 的顶点A在第二象限，与y轴交于点B，对称轴为直线l， $B C ⊥ l$ 于点C，点A与点E关于 $B C$ 的中点D成中心对称，以点E为顶点的抛物线 $y = a_{2} x^{2} + b_{2} x + c_{2} (a_{2} < 0)$ 经过点D，则 $\frac{a_{2}}{a_{1}}$ 的值为．

查看试题解析
14. 在平面直角坐标系中，若点 $A (3 ， 2)$ 与点 $B (m ， - 2)$ 关于原点对称，则m的值是．

查看试题解析

三、解答题

15. 在4×4的方格纸中，△ABC的三个顶点都在格点上．

(1)、在图1中画出与△ABC成轴对称且与△ABC有公共边的格点三角形（画出一个即可）；

(2)、将图2中的△ABC绕着点C按顺时针方向旋转90°，画出经旋转后的三角形．

查看试题解析
16. 如图，四边形ABCD在平面直角坐标系中，

(1)、分别写出点A、B、C、D各点的坐标；

(2)、作出四边形ABCD关于原点O对称的四边形A′B′C′D′，并写出各顶点坐标．

查看试题解析
17. 如图，在5×7的正方形网格中，每个小正方形的边长均为1，每个小正方形顶点叫做格点，△ABC的顶点都在格点上，将△ABC绕着点O顺时针旋转90°得到△A′B′C′，请在图中画出旋转后的△A′B′C′．

查看试题解析
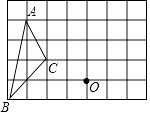18.
如图：三角形DEF是三角形ABC经过某种变换后得到的图形，分别写出点A与点D，点B与点E，点C与点F的坐标，并观察它们的关系，如果三角形ABC中任一点M的坐标（x，y），那么它的对应点N的坐标是什么？

查看试题解析
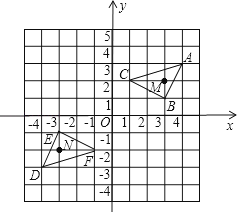19.
如图，点A坐标为（﹣2，3），将点A绕原点O顺时针旋转90°得点A′，求A′的坐标．

查看试题解析
20.
如图，直线y=﹣ $\frac{4}{3}$ x+4与x轴、y轴分别交于A、B两点，把△A0B绕点A顺时针旋转90°后得到△AO′B′，求点B′的坐标．

查看试题解析
21. 直角坐标系第二象限内的点P（x²+2x，3）与另一点Q（x+2，y）关于原点对称，试求x+2y的值．

查看试题解析
22.
△ABO在平面直角坐标系的位置如图1所示，其中，点A（4，2）、B（3，0）、O（0，0）．
（1）将△ABO绕原点O逆时针旋转90°得△A₁B₁O，在图1中画出旋转后的图形，其中点A₁的坐标是
（2）将△A₁B₁O向x轴正方向平移3个单位得△A₂B₂B，B₂B与OA交于点M，在图2中画出图形，并证明：MB平分∠A₂BA；
（3）求△ABM的面积．

查看试题解析
23.
如图，在边长为1个单位长度的小正方形组成的网格中，给出了格点△ABC（顶点是网格线的交点）．
（1）将△ABC绕点B顺时针旋转90°得到△A′BC′，请画出△A′BC′．
（2）求BA边旋转到B′A′位置时所扫过图形的面积．

查看试题解析
24.
如图将△ABC沿x轴的正方向平移4单位得到△A′B′O′，再绕O′点按顺时针旋转90°得到△A″B″O″，若A的坐标为（﹣2，3），B点坐标为（﹣3，0）；
①在图中画△A′B′O′和△A″B″O″；
②直接写出A′和A″点的坐标；
③△ABO的顶点A在变换过程中所经过的路径长为多少？

查看试题解析

（人教版）2023-2024学年九年级上学期数学 23.2 中心对称 期末复习(吉林地区专用)

一、选择题

二、填空题

三、解答题

（人教版）2023-2024学年九年级上学期数学 23.2 中心对称期末复习(吉林地区专用)