(人教版)2023-2024学年九年级上学期数学 23.1 图形的旋转 期末复习(吉林地区专用)
试卷更新日期:2023-12-20 类型:复习试卷
一、选择题
-
1. 如图,在平面直角坐标系中,△ABC绕点C(0,1)旋转180°得到△A'B'C,已知点A的坐标为(2,-1).则点A'的坐标是.( )
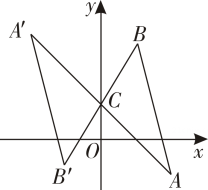 A、(- 2,1) B、(-2,3) C、(-2,-1) D、(-2,2)2. 如图,把△ABC绕C点顺时针旋转35°,得到△A'B'C,A'B'交AC于点D, 若∠A'DC=90°,则∠A的度数( )
A、(- 2,1) B、(-2,3) C、(-2,-1) D、(-2,2)2. 如图,把△ABC绕C点顺时针旋转35°,得到△A'B'C,A'B'交AC于点D, 若∠A'DC=90°,则∠A的度数( )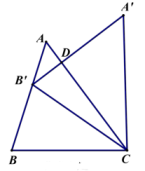 A、35° B、75° C、55° D、65°3. 如图,△ABC中,∠BAC=135°,把△ABC绕着点C顺时针旋转得到△DEC,若点D、A、B恰好在一条直线上,则下列结论错误的是 ( )
A、35° B、75° C、55° D、65°3. 如图,△ABC中,∠BAC=135°,把△ABC绕着点C顺时针旋转得到△DEC,若点D、A、B恰好在一条直线上,则下列结论错误的是 ( )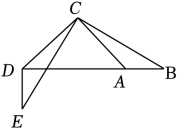 A、ED⊥BD B、△ABC≌△DEC C、 D、BD=CE+DE4. 如图所示的正六边形花环绕中必至少旋转度能与自身重合,则为( )
A、ED⊥BD B、△ABC≌△DEC C、 D、BD=CE+DE4. 如图所示的正六边形花环绕中必至少旋转度能与自身重合,则为( )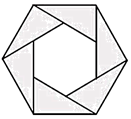 A、30 B、60 C、120 D、1805. 国旗上的五角星是旋转对称图形,它需要旋转( )后,才能与自身重合.A、36° B、45° C、60° D、72°6. 如图,边长为1的正方形ABCD绕点A逆时针旋转45°后,得到正方形AB′C′D′,边B'C′与DC交于点O,则∠DOB'的度数为( )
A、30 B、60 C、120 D、1805. 国旗上的五角星是旋转对称图形,它需要旋转( )后,才能与自身重合.A、36° B、45° C、60° D、72°6. 如图,边长为1的正方形ABCD绕点A逆时针旋转45°后,得到正方形AB′C′D′,边B'C′与DC交于点O,则∠DOB'的度数为( )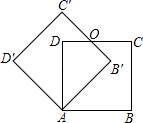 A、125° B、130° C、135° D、140°7. 如图,平面直角坐标系中,点B在第一象限,点A在x轴的正半轴上, , , 将绕点O逆时针旋转 , 点B的对应点的坐标是( )
A、125° B、130° C、135° D、140°7. 如图,平面直角坐标系中,点B在第一象限,点A在x轴的正半轴上, , , 将绕点O逆时针旋转 , 点B的对应点的坐标是( )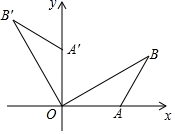 A、 B、 C、 D、8. 如图,在△ABC中,∠ACB=90°,∠B=30°,AB=4,将△ABC绕点A顺时针旋转得到△AB'C',当点C'落在边AB上时,线段CC'的长为( )
A、 B、 C、 D、8. 如图,在△ABC中,∠ACB=90°,∠B=30°,AB=4,将△ABC绕点A顺时针旋转得到△AB'C',当点C'落在边AB上时,线段CC'的长为( )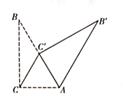 A、 B、1 C、 D、2
A、 B、1 C、 D、2二、填空题
-
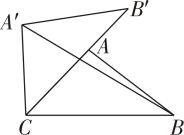
9. 如图,将△ABC绕点C逆时针旋转得到△A'B'C',其中点A'与点A是对应点,点B'与点B是对应点,点B'落在边AC上,连结A'B.若∠ACB=45°,AC=2.BC=4,则∠A'B= °
 10. 如图,在等边△ABC中,点D是边AC上一点,将△BCD绕点B逆时针旋转60°得到△BAE,若BC=8,BD=6,则OAED的周长为
10. 如图,在等边△ABC中,点D是边AC上一点,将△BCD绕点B逆时针旋转60°得到△BAE,若BC=8,BD=6,则OAED的周长为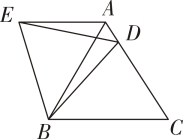 11. 如图,该图形绕其中心旋转能与自身完全重合.则其旋转角最小为度.
11. 如图,该图形绕其中心旋转能与自身完全重合.则其旋转角最小为度.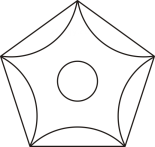 12. 如图所示的图形绕其中心至少旋转度就可以与原图形完全重合.
12. 如图所示的图形绕其中心至少旋转度就可以与原图形完全重合.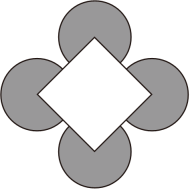 13. 如图,将绕点顺时针旋转角 , 得到 , 若 , , 则的度数为 .
13. 如图,将绕点顺时针旋转角 , 得到 , 若 , , 则的度数为 .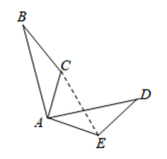 14. 如图,E是正方形ABCD内一点,将△ABE绕点B顺时针旋转与△CBF重合,若BE= , 则EF=
14. 如图,E是正方形ABCD内一点,将△ABE绕点B顺时针旋转与△CBF重合,若BE= , 则EF=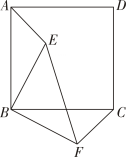
三、解答题
-
15. 如图,将矩形ABCD绕点A顺时针旋转得到矩形AB'C'D' ,点C的对应点C'恰好落在CB的延长线上,边AB与C'D'相交于点E.求证:BC=BC'.
 16. 如图,在△ABC中,AB=2,BC=3.6.∠B=60°,将△ABC绕点A按顺时针方向旋;转一定角度得到△ADK,当点B的对应点D恰好落在BC边上时,求CD的长.
16. 如图,在△ABC中,AB=2,BC=3.6.∠B=60°,将△ABC绕点A按顺时针方向旋;转一定角度得到△ADK,当点B的对应点D恰好落在BC边上时,求CD的长.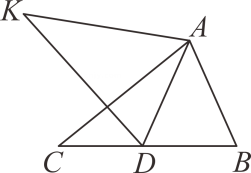 17. 如图,在中, , 以点为旋转中心,把逆时针旋转 , 得到 , 连接 , 求的长.
17. 如图,在中, , 以点为旋转中心,把逆时针旋转 , 得到 , 连接 , 求的长.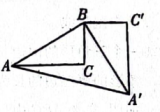 18. 如图,在Rt△ABC中,∠C=90°,∠BAC=30°,BC=2,以点B为旋转中心,把Rt△ABC逆时针旋转90°,得到△A'BC',连接AA',求AA'的长,
18. 如图,在Rt△ABC中,∠C=90°,∠BAC=30°,BC=2,以点B为旋转中心,把Rt△ABC逆时针旋转90°,得到△A'BC',连接AA',求AA'的长,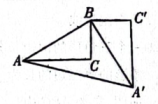 19. 如图,在△ABD中,∠BAD=90°,将△ABD绕点A逆时针旋转后得到△ACE,C点落在BD边上,若∠E=17°,求∠BAC的度数.
19. 如图,在△ABD中,∠BAD=90°,将△ABD绕点A逆时针旋转后得到△ACE,C点落在BD边上,若∠E=17°,求∠BAC的度数.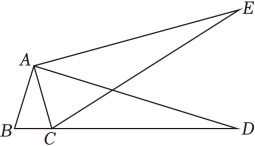 20. 如图,在Rt△ABC中,∠C= 90°,将△ABC绕着点B逆时针旋转得到△FBE,点C,A的对应点分别为E,F,点F落在BA上,连接AF.
20. 如图,在Rt△ABC中,∠C= 90°,将△ABC绕着点B逆时针旋转得到△FBE,点C,A的对应点分别为E,F,点F落在BA上,连接AF.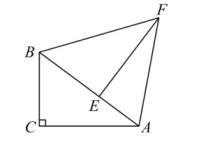 (1)、若∠BAC=40°,则∠AFE的度数为(2)、若AC=8,BC=6,求AF的长.21. 如图,在△ABC中,∠B=20°,∠ACB= =30°,AB=2 cm,△ABC逆时针旋转一定角度后与△ADE重合,且点C恰好成为AD的中点.
(1)、若∠BAC=40°,则∠AFE的度数为(2)、若AC=8,BC=6,求AF的长.21. 如图,在△ABC中,∠B=20°,∠ACB= =30°,AB=2 cm,△ABC逆时针旋转一定角度后与△ADE重合,且点C恰好成为AD的中点.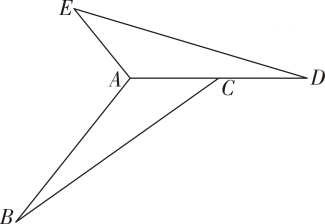 (1)、指出旋转中心,并求出旋转的度数;(2)、求出∠BAE的度数和AE的长.22. 如图所示,在中, , 将绕点A逆时针旋转至处,使点B落在BC延长线上的D点处,求的度数.
(1)、指出旋转中心,并求出旋转的度数;(2)、求出∠BAE的度数和AE的长.22. 如图所示,在中, , 将绕点A逆时针旋转至处,使点B落在BC延长线上的D点处,求的度数.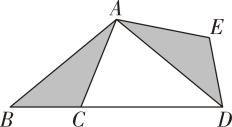 23. 如图,四边形是正方形,点为内一点,将绕点顺时针旋转得到 , 连接、、 , 与交于点 .
23. 如图,四边形是正方形,点为内一点,将绕点顺时针旋转得到 , 连接、、 , 与交于点 .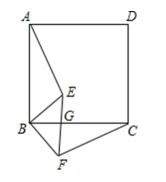 (1)、求证:;(2)、若 , 求的大小.24. 我们可以通过类比联想,引申拓展研究典型题目,可达到解一题知一类的目的,下面是一个案例,请补充完整.
(1)、求证:;(2)、若 , 求的大小.24. 我们可以通过类比联想,引申拓展研究典型题目,可达到解一题知一类的目的,下面是一个案例,请补充完整.原题:如图1,点E、F分别在正方形ABCD的边BC、CD上, , 连接EF , 则 , 试说明理由.
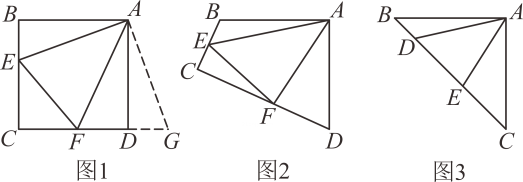 (1)、思路梳理
(1)、思路梳理,
把绕点A逆时针旋转至 , 可使AB与AD重合.
,
, 点F、D、G共线.
根据 , 易证 , 得 .
(2)、类比引申如图2,四边形ABCD中, , , 点E、F分别在边BC、CD上, , 若、都不是直角,则当与满足等量关系时,仍有 .
(3)、联想拓展如图3,在中, , , 点D、E均在边BC上,且 . 猜想BD、DE、EC应满足的等量关系,并写出推理过程.