北京市大兴区2023-2024学年八年级上学期期中数学试卷

试卷更新日期：2023-12-20 类型：期中考试

进入出卷网下载

一、选择题（共16分，每题2分）第1-8题均有四个选项，符合题意的选项只有一个

1. 下列图形不是轴对称图形的为（　　）

A、线段 B、角 C、有一个锐角为30°的直角三角形 D、等边三角形

查看试题解析
2. 下列各组线段的长，能组成三角形的是（　　）

A、6，7，14 B、5，6，10 C、4，4，8 D、3，4，8

查看试题解析
3. 下面四个图形中，线段BE是△ABC的高的图是（）

A、 B、 C、 D、

查看试题解析
4. 有一个内角是36°的等腰三角形，其它两个内角的度数分别是（　　）

A、36°，36° B、36°，72° C、36°，108°或72°，72° D、36°，144°

查看试题解析
5. 如图，Rt△ACB中，∠ACB＝90°，∠A＝15°，AB的垂直平分线与AC交于点D，与AB交于点E，连接BD．若AD＝14，则BC的长为（　　）

A、4 B、5 C、6 D、7

查看试题解析
6. 如图，在3×3的正方形网格中有四个格点A ， B ， C ， D ，以其中一个点为原点，网格线所在直线为坐标轴，建立平面直角坐标系，使其余三个点中存在两个点关于一条坐标轴对称，则原点可能是（）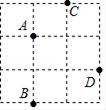

A、点A B、点B C、点C D、点D

查看试题解析
7. 已知，△ABC和△ADC关于直线AC轴对称，如果∠BAD＋∠BCD＝160°，那么△ABC是（　　）

A、直角三角形 B、等腰三角形 C、钝角三角形 D、锐角三角形

查看试题解析
8. 在△ABC中，∠ABC、∠ACB的角平分线交于点O，若90°＜∠BOC＜120°，则∠A的取值范围是（　　）

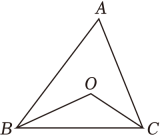A、0°＜∠A＜30° B、10°＜∠A＜30° C、0°＜∠A＜60° D、10°＜∠A＜60°

查看试题解析

二、填空题（共16分，每题2分）

9. 点P（﹣2，3）关于y轴对称的点的坐标是．

查看试题解析
10. 等腰三角形两边长分别为6和8，则这个等腰三角形的周长为

查看试题解析
11. 一个多边形的内角和跟它的外角和相等，则这个多边形是边形．

查看试题解析
12. 如图，在△ABC中，点D、E分别是BC、AB边上的中点，若△ADE的面积是2，则△ABC的面积是．

查看试题解析
13. 如图，在△ABC中，∠A＝89°，∠B＝40°，则∠ACD＝°．

查看试题解析
14. 如图，在△ABC中，BD是边AC上的高，CE平分∠ACB，交BD于点E，DE＝2，BC＝6，则△BCE的面积为．

查看试题解析
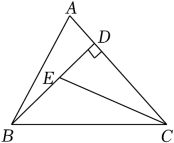15. 如图，△ABC中，AB=AC，D是BC的中点，AC的垂直平分线分别交AC、AD、AB于点E、O、F，则图中全等的三角形的对数是．

查看试题解析
16. 在平面直角坐标系xOy中，已知点A（2，3），在坐标轴上找一点P，使得△AOP是等腰三角形，则这样的点P共有个．

查看试题解析

三、解答题（本题共68分，第17-23题每题5分，第24-25每题6分，第26-28每题7分）

17. 如图，画出△ABC关于y轴对称的△A₁B₁C₁ ，并写出A₁、B₁、C₁各顶点的坐标：A₁ ▲ ， B₁ ▲ ， C₁ ▲ ．

查看试题解析
18. 把下列证明过程补充完整．
已知：如图，点A，B，C，D在同一条直线上，AB＝CD，∠E＝∠F，EC∥FB．
求证：EA＝FD．
证明：∵AB＝CD（已知），
∴AB+BC＝CD+BC．
∴AC＝DB．
∵EC∥FB（已知），
∴∠1＝∠2（     ▲    ）．
在△AEC和△DFB中，
${\begin{cases} ∠ E = ∠ F \\ ∠ 1 = ∠ 2 \\ A C = D B \end{cases}$ ，
∴△AEC≌△DFB（     ▲    ）．
∴EA＝FD（     ▲    ）．

查看试题解析
19. 把下列证明过程补充完整．
已知：如图，AC＝AD，∠C＝∠D，∠1＝∠2．
求证：AB＝AE．
证明：∠1＝∠2，
∴∠1+∠BAD＝∠2+∠BAD．
∴∠ ▲ ＝∠EAD．
在△ABC和△AED中，
${\begin{cases} () \\ () \\ ∠ （） = ∠ E A D \end{cases}$ ．
∴ ▲ ．
∴AB＝AE．

查看试题解析
20. 把下列证明过程补充完整．
已知：如图，四边形ABCD中，AB＝AD，∠B＝∠D＝90°．
求证：AC平分∠BAD．
证明：∵∠B＝∠D＝90°．
∴在Rt△ABC和Rt△ADC中，
${\begin{cases} （） \\ A B = A D \end{cases}$ ，
∴Rt△ABC≌Rt△ADC（ ▲ ）．
∴∠ ▲ ＝∠ ▲ ．
∴AC平分∠BAD．

查看试题解析
21. 把下列证明过程补充完整．
已知：如图，在△ABC中，AB＝AC，AD是BC边上的中线，CE⊥AB于点E．
求证：∠CAD＝∠BCE．
证明：∵AB＝AC，
∴∠B＝∠    ▲     ，
∵AD是BC边上的中线，
∴AD    ▲    BC（三线合一）．
∴∠ADC＝90°．
∴∠CAD+∠ACB＝90°，
∵CE⊥AB，
∴∠BEC＝90°．
∵∠    ▲    +∠B＝90°，
∴∠CAD＝∠BCE．

查看试题解析
22.
如图，△ABC中，AD⊥BC于点D，AD=BD，∠C=65°，求∠BAC的度数．

查看试题解析
23. 已知：如图，D是BC上一点，AB＝BD，DE∥AB，∠A＝∠DBE．
求证：AC＝BE．

查看试题解析
24. 如图，在四边形ABCD中，AB=BC，BF平分∠ABC，AF∥DC，连接AC，CF.求证：

(1)、AF=CF；

(2)、CA平分∠DCF.

查看试题解析
25. 已知：如图，点A，B分别在线段CD，CE上，EA，DB分别为线段CD，CE的垂直平分线．求∠AEC的度数．

查看试题解析
26. 已知： $\frac{5}{5 - 4} + \frac{8 - 5}{4 - 5}$ ＝2，…， $\frac{6}{6 - 4} + \frac{8 - 6}{4 - 6}$ ＝2，…， $\frac{9}{9 - 4} + \frac{8 - 9}{4 - 9}$ ＝2，…， $\frac{11}{11 - 4} + \frac{8 - 11}{4 - 11}$ ＝2⋯

(1)、观察上面式子的规律，把这个规律用含字母a的式子表示是；

(2)、若（1）中的a是△ABC的一边长，且4，8是△ABC的另两边长，
①a的取值范围是；
②当△ABC是等腰三角形时，按上述规律对应的等式是．

查看试题解析
27. 如图，在△ABC中，AB＝AC，D是BC中点，∠BAC＝60°，BC＝1，点E，F分别在AB，AC边上，且∠AED+∠AFD＝180°．

(1)、用等式表示线段DE与DF的数量关系，并证明；

(2)、求AE+AF的长．

查看试题解析
28. 对于平面直角坐标系xOy内的点P和图形M，给出如下定义：连接OP，过点O作OP的垂线OW，在垂线OW上取一点P′，使OP′＝OP，点P′在图形M上或图形M围成的区域内，那么称点P是图形M关于原点O的“关联垂点”．已知点A（1，1），B（3，1），C（2，3）．

(1)、在点P₁（﹣1，0），P₂（﹣1，1），P₃（﹣1，2），P₄（﹣1，3）中，点是线段AB关于原点O的“关联垂点”（只填写字母）；

(2)、如果点D（m，2）是△ABC关于原点O的“关联垂点”，求m的取值范围．

查看试题解析