重庆市潼南区六校2023-2024学年八年级上学期期中数学试卷

试卷更新日期：2023-12-20 类型：期中考试

进入出卷网下载

一、选择题（共10小题，每题4分，共40分）

1. 5的倒数是（　　）

A、5 B、﹣5 C、 $\frac{1}{5}$ D、 $- \frac{1}{5}$

查看试题解析
2. 下列说法中，不正确的是（　　）

A、全等三角形对应角相等 B、全等三角形对应边上的高相等 C、有两边和一角对应相等的两个三角形全等 D、有两角和一边对应相等的两个三角形全等

查看试题解析
3. 下列每组数分别表示三根木棒的长度，将它们首尾连接后，能摆成三角形的一组是( )

A、1，2，6 B、2，2，4 C、1，2，3 D、2，3，4

查看试题解析
4. 下列各图中，作△ABC边AC边上的高，正确的是（　　）

A、 B、 C、 D、

查看试题解析
5. 如图，AD是△ABC的中线，AB＝5，AC＝4．若△ACD的周长为10，则△ABD的周长为（　　）

A、8 B、9 C、10 D、11

查看试题解析
6. 估计 $\sqrt{7} + 5$ 的值应在（　　）

A、6和7之间 B、7和8之间 C、8和9之间 D、9和10之间

查看试题解析
7. 用圆圈按如图所示的规律拼图案，其中第①个图案中有2个圆圈，第②个图案中有5个圆圈，第③个图案中有8个圆圈，第④个图案中有11个圆圈，…，按此规律排列下去，则第⑦个图案中圆圈的个数为（）

A、14 B、20 C、23 D、26

查看试题解析
8. 如图，∠1、∠2、∠3是五边形ABCDE的三个外角，边AE、CD的延长线相交于点F ，如果∠F＝α，那么∠1+∠2+∠3的度数为（　　）

A、270°﹣α B、360°﹣α C、90°+α D、180°+α

查看试题解析
9. 如图， $△ A B C$ 中， $∠ A C F$ 、 $∠ E A C$ 的角平分线 $C P$ 、 $A P$ 交于点 $P$ ，延长 $B A$ 、 $B C$ ， $P M ⊥ B E$ ， $P N ⊥ B F .$ 则下列结论中正确的个数（）
$① B P$ 平分 $∠ A B C$ ； $② ∠ A B C + 2 ∠ A P C = 180 °$ ； $③ ∠ C A B = 2 ∠ C P B$ ； $④ S_{△ P A C} = S_{△ M A P} + S_{△ N C P}$ ．

A、 $1$ 个 B、 $2$ 个 C、 $3$ 个 D、 $4$ 个

查看试题解析
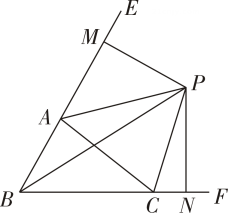10. 在多项式x-y-z-m-n（其中x＞y＞z＞m＞n）中，对相邻的两个字母间任意添加绝对值符号，添加绝对值符号后仍只有减法运算，然后进行去绝对值运算，称此为“绝对操作”．例如：x-y-|z-m|-n＝x-y-z+m-n ， |x-y|-z-|m-n|＝x-y-z-m+n ， …．下列说法：
①存在“绝对操作”，使其运算结果与原多项式相等；
②不存在“绝对操作”，使其运算结果与原多项式之和为0；
③所有的“绝对操作”共有7种不同运算结果．
其中正确的个数是（　　）

A、0 B、1 C、2 D、3

查看试题解析

二、填空题（共8小题，每小题4分。共32分）

11. 已知一个等腰三角形的两边长分别为2和4，则该等腰三角形的周长是．

查看试题解析
12. 起重机的吊臂中有三角形结构，这是利用了三角形的.

查看试题解析
13. 若正多边形的一个外角是60°，则这个正多边形的内角和是．

查看试题解析
14. 如图，AD＝AE ， ∠1＝∠2，请你添加一个条件（只填一个即可），使△ABD≌△ACE ．

查看试题解析
15. 如图，已知AD∥BC ， ∠BAD与∠ABC的平分线相交于点P ，过点P作EF⊥AD ，交AD于点E ，交BC于点F ， EF＝4cm ， AB＝5cm ，则△APB的面积为 cm² ．

查看试题解析
16. 如图，在△ABC中，已知点D ， E ， F分别为边BC ， AD ， CE的中点，且 $S_{△ A B C} = 8 c m^{2}$ ，则阴影部分的面积等于．

查看试题解析
17. 若关于x的不等式组 ${\begin{cases} \frac{3 x - 1}{2} - 3 \leq \frac{6 - x}{3} \\ 2 a - 7 x < 15 \end{cases}$ ，有且只有3个整数解，且关于y的一元一次方程2y+6＝3a的解是正整数，则所有满足条件的整数a的值之和为．

查看试题解析
18. 如果一个三位自然数各个数位上的数字均不为0，且十位数字等于百位数字与个位数字的和，则称这个数为“十佳数”．如：352，∵5＝3+2，∴352是“十佳数”．又如：234，∵3≠2+4，∴234不是“十佳数”．已知M是一个“十佳数”，则M的最大值为；交换M的百位数字和十位数字得到一个三位数N ，在N的末位数字后添加数字1得到一个四位数P ，在M的十位数字与个位数字之间添加M的百位数字得到一个四位数Q ，若P﹣Q能被11整除，则满足以上条件的“十佳数”M的最小值为．

查看试题解析

三、解答题（本小题共8小题，19题8分，20-26小题每小题10分，共78分）

19.

(1)、解方程组： ${\begin{cases} 3 x + y = 2 \\ 2 x - 3 y = 21 \end{cases}$ ；

(2)、 $- 1^{2023} - | \sqrt{2} - 2 | + \sqrt[3]{8}$ ．

查看试题解析
20. 如图，Rt△ABC中，∠ACB＝90°．

(1)、尺规作图：在斜边AB上找一点D ，使AD＝AC ，作∠BAC的平分线，交BC于点E ，连结DE；（不写作法，保留作图痕迹）

(2)、在（1）的条件下，求证：△BDE是直角三角形．
证明：∵AE平分∠BAC ，
∴　 ▲ 　＝　 ▲ 　，
在△ACE和△ADE中，
${\begin{cases} () = () \\ ∠ () = ∠ () \\ A E = A E \end{cases}$ ，
∴△ACE≌△ADE ，
∵∠ACB＝90°，
∴　 ▲ 　＝∠ACB＝90°，
∴∠BDE＝90°，△BDE是直角三角形．

查看试题解析
21. 重庆市2023年体育中考已经结束，现从某校初三年级随机抽取部分学生的成绩进行统计分析（成绩得分用x表示，共分成4个等级，A：30≤x＜35，B：35≤x＜40，C：40≤x＜45，D：45≤x≤50），绘制了如下的统计图，请根据统计图信息解答下列问题：

(1)、本次共调查了名学生；

(2)、请补全条形统计图；

(3)、在扇形统计图中，m的值是；B对应的扇形圆心角的度数是；

(4)、若该校初三年级共有2000名学生，估计此次测试成绩优秀（45≤x≤50）的学生共有多少人？

查看试题解析
22. 如图，点A ， B ， C ， D在同一直线上，AB＝CD ， AE∥DF ， EC∥BF ．

(1)、求证：AE＝DF；

(2)、若AD＝8，BC＝2，求AC的长．

查看试题解析
23. 新能源汽车因其废气排放量比较低，被越来越多的家庭所喜爱，某汽车专卖店销售甲、乙两种型号的新能源汽车，某月的第一周售出1辆甲型车和3辆乙型车，销售额为65万元；第二周售出4辆甲型车和5辆乙型车，销售额为155万元．

(1)、求每辆甲型车和乙型车的售价各为多少万元？

(2)、某公司准备向该汽车专卖店购买甲、乙两种型号的新能源汽车共8辆，其购车费用不少于145万元，且不超过153万元，问有哪几种购车方案？从公司节约的角度考虑，你会选择哪种购车方案？

查看试题解析
24. 如图，在△ABC中，∠C＞∠B ， AD平分∠BAC ，点M为线段AD上一动点（不与A ， D重合），MN⊥BC于N ．

(1)、若∠B＝38°，∠DMN＝10°，求∠C的度数；

(2)、当点M在AD上移动时，直接写出∠B ， ∠C ， ∠DMN之间的数量关系．

查看试题解析
25. 如图，△ABC中，AD是BC边上的中线，E ， F为直线AD上的点，连接BE ， CF ，且BE∥CF ．

(1)、求证：△BDE≌△CDF；

(2)、若AE＝13，AF＝7，试求DE的长．

查看试题解析
26. 请完成下面的说明：

(1)、如图①所示，△ABC的外角平分线交于点G ，试说明∠BGC＝90°﹣ $\frac{1}{2}$ ∠A ．

(2)、如图②所示，若△ABC的内角平分线交于点I ，试说明∠BIC＝90°+ $\frac{1}{2}$ ∠A ．

(3)、根据（1），（2）的结论，你能说出∠BGC和∠BIC的关系吗？

查看试题解析