（人教版）2023-2024学年九年级上学期数学 22.2 二次函数与一元二次方程期末复习(吉林地区专用)

试卷更新日期：2023-12-20 类型：复习试卷

进入出卷网下载

一、选择题

1. 二次函数 $y = a x^{2} + b x + c$ 的部分图象如图所示，对称轴为 $x = - 1$ ，图象与 $x$ 轴相交于点 $(1 ， 0)$ ，则方程 $a x^{2} + b x + c = 0$ 的根为（）

A、 $x_{1} = 1 ， x_{2} = - 3$ B、 $x_{1} = - 1 ， x_{2} = 3$ C、 $x_{1} = 1 ， x_{2} = - \frac{1}{3}$ D、 $x_{1} = - 1 ， x_{2} = \frac{1}{3}$

查看试题解析
2. 如图，不考虑空气阻力，以一定的速度将小球沿斜上方击出时，小球飞行的高度是飞行时间的二次函数．现以相同的初速度沿相同的方向每隔t秒依次击出三个质地一样的小球，小球在各自击出后2秒到达相同的最大飞行高度，若整个过程中，保持空中始终有1或2个小球（不考虑小球落地后再弹起），则t的取值范围是（　　）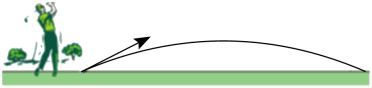

A、0＜t＜2 B、2≤t＜4 C、1≤t＜3 D、3≤t＜5

查看试题解析
3. 根据下列表格中的对应值，判断方程 $a x^{2} + b x + c = 0$ （ $a \neq 0$ ， a，b，c为常数）的根的个数是（）
$x$
6.17
6.18
6.19
6.20
$y = a x^{2} + b x + c$
0.02
-0.01
0.02
0.04

A、0 B、1 C、2 D、1或2

查看试题解析
4. 如图，二次函数y＝ax²+bx+c（a＜0）的图象经过原点O，与x轴另一个交点为A点，则方程ax²+bx+c＝0的解是（　　）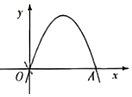

A、两个正根 B、两个负根 C、一个正根，一个负根 D、0和一个正根

查看试题解析
5. 二次函数y＝ax²+bx+c（a≠0，a、b、c为常数）的图象如图所示，则方程ax²+bx+c＝m有实数根的条件是（）

A、m≥﹣4 B、m≥0 C、m≥5 D、m≥6

查看试题解析

6. 观察下列表格，一元二次方程x²﹣x﹣1.1=0的最精确的一个近似解是（　　）

x	1.1	1.2	1.3	1.4	1.5	1.6	1.7	1.8	1.9
x²﹣x﹣1.1	﹣0.99	﹣0.86	﹣0.71	﹣0.54	﹣0.35	﹣0.14	0.09	0.34	0.61

A、0.09 B、1.1 C、1.6 D、1.7

查看试题解析

7.
已知二次函数y=ax²+bx+c的图象如图所示，则一元二次方程ax²+bx+c=0的近似解为（　　）

A、x₁≈﹣2.1，x₂≈0.1 B、x₁≈﹣2.5，x₂≈0.5 C、x₁≈﹣2.9，x₂≈0.9 D、x₁≈﹣3，x₂≈1

查看试题解析
8. 二次函数y=ax²+bx+c（a≠0）的函数值y与自变量x的四组对应值如表所示：则方程ax²+bx+c=0的根的个数是（　　）
       x
     6.15
    6.18
    6.21
     6.24
       y
     0.02
﹣0.01
    0.02
     0.11

A、0 B、1 C、2 D、不能确定

查看试题解析

二、填空题

9. 如图，已知二次函数y＝ax²+bx+c的图象过点（3，0），对称轴为直线x＝1，则下列结论：①abc＜0；②ax²+bx+c＝0的两个根是x₁＝-1，x₂＝3；③当x＜1时，y随着x的增大而增大；④4a+2b+c＜0．（填写序号）．

查看试题解析
10. 在平面直角坐标系中，抛物线 $y = a x^{2} - 4 a x - 1$ 经过点 $(2 ， 7)$ ．若关于 $x$ 的一元二次方程 $a x^{2} - 4 a x - 1 - t = 0$ （ $t$ 为实数）在 $\frac{1}{2} < x < 4$ 的范围内有实数根，则 $t$ 的取值范围为.

查看试题解析
11. 二次函数 $y = x^{2} + b x$ 的对称轴为x=1，若关于x的一元二次方程 $x^{2} + b x - c = 0$ （c为实数），在-1≤x≤4范围内有解，则c的取值范围为．

查看试题解析
12. 如图，在平面直角坐标系中，抛物线 $y = a x^{2} + 3 (a < 0)$ 与y轴交于点A，过点A作x轴的平行线交抛物线 $y = \frac{1}{2} x^{2}$ 于点B、C，则线段BC的长为．

查看试题解析
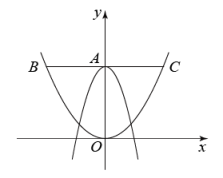13. 二次函数 $y = x^{2} + b x$ 的对称轴为 $x = - 1$ ，若关于x的一元二次方程 $x^{2} + b x - t = 0$ (t为实数)在-4<x<1的范围内有解，则t的取值范围是．

查看试题解析
14. 如图，在平面直角坐标系中，点 $A (2 ， 4)$ 在抛物线 $y = a x^{2}$ 上，过点A作y轴的垂线，交抛物线于另一点B ，点C、D在线段AB上，分别过点C、D作x轴的垂线交抛物线于E、F两点．当四边形CDFE为正方形时，线段CD的长为．

查看试题解析

三、解答题

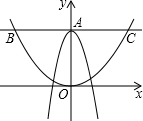
15. 如图，在平面直角坐标系中，抛物线y=ax²+3与y轴交于点A ，过点A与x轴平行的直线交抛物线 $y = \frac{1}{3} x^{2}$ 于点B、C ，求BC的长.

查看试题解析
16. 如果函数y=（a﹣1）x²+3x+ $\frac{a + 5}{a - 1}$ 的图象经过平面直角坐标系的四个象限，求a的取值范围．

查看试题解析
17. 一元二次方程x²+7x+9=1的根与二次函数y=x²+7x+9的图象有什么关系？试把方程的根在图象上表示出来．

查看试题解析
18. 利用函数的图象，求方程x²=2x+3的解．

查看试题解析
19. 小明在复习数学知识时，针对“求一元二次方程的解”整理了以下几种方法，请你将有关内容补充完整：
例题：求一元二次方程x²﹣x﹣1=0的两个解．

(1)、解法一：（1）选择合适的一种方法（公式法、配方法、分解因式法）．

(2)、
（2）解法二：利用二次函数图象与坐标轴的交点求解，如图（1）所示，①把方程x²-x-1=0的解看成是二次函数y= 的图象与x 轴交点的横坐标，即x₁ ， x₂就是方程的解。②画出这两个函数的图象，用x₁ ， x₂在x轴上标出方程的解。

查看试题解析
20. 如图，抛物线y= $- \frac{2}{3}$ x²+bx+c与x轴交于点A和点B（3，0），与y轴交于点C（0，2），点D是抛物线上一动点．

(1)、求抛物线的解析式；

(2)、如图①，当点D在直线BC上方时，作DF上x轴于点F，交直线BC于点E，当∠D=∠BCO时，求点D的坐标；

(3)、点P在抛物线的对称轴l上，点Q是平面直角坐标系内一点，当四边形BPDQ是正方形时，请直接写出点P的坐标．

查看试题解析

21. 小明发现某乒乓球发球器有“直发式”与“间发式”两种模式，在“直发式”模式下，球从发球器出口到第一次接触台面的运动轨迹近似为一条抛物线；在“间发式”模式下，球从发球器出口到第一次接触台面的运动轨迹近似为一条直线，球第一次接触台面到第二次接触台面的运动轨迹近似为一条抛物线

.

如图

1

和图

2

分别建立平面直角坐标系

x O y

．

通过测量得到球距离台面高度 $y ($ 单位： $d m)$ 与球距离发球器出口的水平距离 $x ($ 单位： $d m)$ 的相关数据，如下表所示：
表 $1$ 直发式

$x (d m)$	$0$	$2$	$4$	$6$	$8$	$10$	$16$	$20$	$\dots$
$y (d m)$	$3.84$	$3.96$	$4$	$3.96$	$m$	$3.64$	$2.56$	$1.44$	$\dots$

表 $2$ 间发式

$x (d m)$	$0$	$2$	$4$	$6$	$8$	$10$	$12$	$14$	$16$	$18$	$\dots$
$y (d m)$	$3.36$	$n$	$1.68$	$0.84$	$0$	$1.40$	$2.40$	$3$	$3.20$	$3$	$\dots$

根据以上信息，回答问题：

(1)、表格中

m =

，

n =

；

(2)、求“直发式”模式下，球第一次接触台面前的运动轨迹的解析式；

(3)、若“直发式”模式下球第一次接触台面时距离出球点的水平距离为

d_{1}

， “间发式”模式下球第二次接触台面时距离出球点的水平距离为

d_{2}

，则

d_{1}

d_{2} (

填“

>

”“

=

”或“

<

”

)

．

查看试题解析

22. 已知关于x的一元二次方程x²+x-m=0.

(1)、若方程有两个不相等的实数根，求m的取值范围；

(2)、二次函数y=x²+x-m的部分图象如图所示，求一元二次方程x²+x-m=0的解.

查看试题解析
23. 如图，抛物线 $y = a x^{2} + b x + 3 (a \neq 0)$ 与 $x$ 轴分别交于点 $A (- 1 ， 0)$ ， $B (3 ， 0)$ ，与 $y$ 轴交于点 $C$ ．

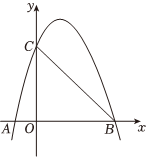(1)、求抛物线的解析式；

(2)、存在正实数 $m$ ， $n (m < n)$ ，当 $m \leq x \leq n$ 时，恰好满足 $\frac{m}{m + 3} \leq \frac{2}{y + 2} \leq \frac{n}{n + 3}$ ，求 $m$ ， $n$ 的值．

查看试题解析
24. 如图1所示的是山西晋城景德桥，是继赵州桥之后我国现存历史悠久的古代珍贵桥梁之一。桥拱面 $O B A$ 可以看作抛物线的一部分（如图2），在某一时刻，桥拱内的水面宽约20米，桥拱顶点B到水面的离为4米。

(1)、如图2，以该时刻水面为x轴，桥拱与水面的一个交点为原点建立直角坐标系，求桥拱部分抛物线的解析式.

(2)、直接写出在距离水面2米处的桥拱宽度为米

(3)、现有两宽为4米，高3米的小舟，相向而行，恰好同时接近拱桥，间两小舟能否同时从桥下穿过，并说明理由。

查看试题解析

$x$	6.17	6.18	6.19	6.20
$y = a x^{2} + b x + c$	0.02	-0.01	0.02	0.04

x	6.15	6.18	6.21	6.24
y	0.02	﹣0.01	0.02	0.11

（人教版）2023-2024学年九年级上学期数学 22.2 二次函数与一元二次方程 期末复习(吉林地区专用)

一、选择题

二、填空题

三、解答题

（人教版）2023-2024学年九年级上学期数学 22.2 二次函数与一元二次方程期末复习(吉林地区专用)