北京市昌平区融合学区（第一组）2023-2024学年九年级上学期期中数学试题

试卷更新日期：2023-12-20 类型：期中考试

进入出卷网下载

一、选择题（共8道小题，每小题2分，共16分）

1. 已知 $3 a = 4 b (a b \neq 0)$ ，则下列比例式中正确的是（）

A、 $\frac{a}{b} = \frac{4}{3}$ B、 $\frac{a}{b} = \frac{3}{4}$ C、 $\frac{a}{3} = \frac{b}{4}$ D、 $\frac{a}{3} = \frac{4}{b}$

查看试题解析
2. 抛物线 $y = x^{2} - 2$ 的顶点坐标是（）

A、 $(0 ， 2)$ B、 $(2 ， 0)$ C、 $(0 ， - 2)$ D、 $(- 2 ， 0)$

查看试题解析
3. 如图，在平行四边形ABCD中，E为BC的中点，连接DE、AC交于点F ，那么 $\frac{E F}{D F}$ 的值为（）

A、 $\frac{1}{3}$ B、 $\frac{1}{2}$ C、 $\frac{2}{3}$ D、1

查看试题解析
4. 将二次函数 $y = x^{2}$ 的图象先向左平移3个单位长度，再向下平移4个单位长度，得到二次函数表达式为（）

A、 $y = {(x + 3)}^{2} - 4$ B、 $y = {(x + 3)}^{2} + 4$ C、 $y = {(x - 3)}^{2} - 4$ D、 $y = {(x - 3)}^{2} + 4$

查看试题解析
5. 如图，已知 $∠ 1 = ∠ 2$ ，那么添加下列一个条件后，不能判定 $△ A B C ∽ △ A D E$ 的是（）

A、 $∠ C = ∠ E$ B、 $∠ B = ∠ A D E$ C、 $\frac{A B}{A D} = \frac{A C}{A E}$ D、 $\frac{A B}{A D} = \frac{B C}{D E}$

查看试题解析
6. 点 $P_{1} (- 1 ， y_{1})$ ， $P_{2} (3 ， y_{2})$ ， $P_{3} (5 ， y_{3})$ ，均在二次函数 $y = {(x - 1)}^{2} + 2$ 的图象上，则 $y_{1}$ ， $y_{2}$ ， $y_{3}$ 的大小关系是（）

A、 $y_{1} > y_{2} > y_{3}$ B、 $y_{3} > y_{1} > y_{2}$ C、 $y_{1} = y_{2} > y_{3}$ D、 $y_{3} > y_{2} = y_{1}$

查看试题解析
7. 下列正方形方格中四个三角形中，与图中的三角形相似的是（）

A、 B、 C、 D、

查看试题解析
8. 如图，正方形ABCD的边长为2cm，点P ， Q同时从点A出发，速度均为2cm/s，若点P沿 $A - D - C$ 向点C运动，点Q沿 $A - B - C$ 向点C运动，则 $△ A P Q$ 的面积 $S (c m^{2})$ 与运动时间 $t (s)$ 之间函数关系的大致图象是（）

A、 B、 C、 D、

查看试题解析

二、填空题（共8道小题，每小题2分，共16分）

9. 如图，直线 $l_{1} ∥ l_{2} ∥ l_{3}$ ，直线AC分别交 $l_{1}$ ， $l_{2}$ ， $l_{3}$ 于点A ， B ， C ，直线DF分别交 $l_{1}$ ， $l_{2}$ ， $l_{3}$ 于点D ， E ， F ，若 $D E = 3$ ， $E F = 6$ ， $A B = 4$ ，则线段 $B C =$ .

查看试题解析
10. 请写出一个开口向下，对称轴为直线 $x = 3$ 的抛物线的解析式．

查看试题解析
11. 二次函数 $y = x^{2} + b x + c$ 图象经过点 $A (0 ， 3)$ ， $B (2 ， 3)$ ，则其对称轴为直线.

查看试题解析
12. 如图，已知 $A (1 ， 4)$ ， $B (3 ， 4)$ ， $C (- 2 ， - 1)$ ， $D (1 ， - 1)$ ，那么 $△ A B E$ 与 $△ C D E$ 的面积比是.

查看试题解析
13. 如图，在 $△ A B C$ 中， $∠ C = 90 °$ ，点D在AC上， $D E ⊥ A B$ 于点E.若 $A C = 4$ ， $A B = 5$ ， $A D = 3$ ，则 $A E =$ .

查看试题解析
14. 抛物线 $y = - x^{2}$ 与抛物线 $y = a x^{2}$ 的位置如图所示，a的值可能为.

查看试题解析
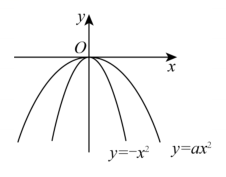15. 如图，小明借助太阳光线测量树高.在早上8时小明测得树的影长为 $2 m$ ，下午3时又测得该树的影长为 $8 m$ ，且这两次太阳光线刚好互相垂直，则树高为 $m$ .

查看试题解析
16. 二次函数 $y = a x^{2} + b x + c (a \neq 0)$ 的图象如图所示，有下列5个结论：
① $a b c > 0$ ；② $b < a + c$ ；③ $4 a + 2 b + c > 0$ ；④ $2 c < 3 b$ ；⑤ $a + b > m (a m + b)$ （ $m \neq 1$ 的实数）.
其中正确的结论有（填序号）.

查看试题解析

三、解答题（本题共12道小题，第17--22题，每小题5分，第23-26题，每小题6分，第27、28题，每小题7分，共68分）

17. 如图，已知四边形 $A B C D ∽$ 四边形 $A^{'} B^{'} C^{'} D^{'}$ .

(1)、 $∠ B =$ .

(2)、求边x ， y的长度.

查看试题解析
18. 已知二次函数 $y = x^{2} + 2 x - 3$ .

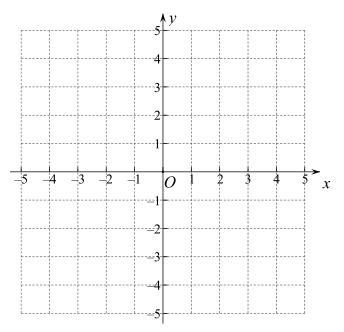(1)、求二次函数的图象的顶点坐标；

(2)、在平面直角坐标系中，画出该函数的图象；

(3)、当x在什么范围时，y随着x的增大而减小？

查看试题解析
19. 如图， $∠ M A N = 30 °$ ，点B、C分别在AM、AN上，且 $∠ A B C = 40 °$ ．

(1)、尺规作图：作∠CBM的角平分线BD，BD与AN相交于点D；（保留作图痕迹，不写作法）

(2)、在（1）所作的图中，求证： $△$ ABC∽ $△$ ADB．

查看试题解析
20. 二次函数 $y = a x^{2} + b x + c (a \neq 0)$ 图象上部分点的横坐标x ，纵坐标y的对应值如下表：
x
…
-3
-2
-1
0
1
2
n
4
…
y
…
15
m
3
0
-1
0
3
8
…

(1)、该二次函数图象的对称轴为直线；

(2)、 $m =$ ， $n =$ ；

(3)、根据表中信息分析，方程 $a x^{2} + b x + c = 0 (a \neq 0)$ 的解为.

查看试题解析
21. 已知二次函数 $y = x^{2} + (2 m + 1) x + m^{2} - 1$ 的图象与x轴有两个交点.

(1)、求m的取值范围；

(2)、写出一个符合条件的m的值，并求出此时图象与x轴的交点坐标.

查看试题解析
22. 如图，抛物线与x轴交于点 $A (- 4 ， 0)$ ， $B (2 ， 0)$ ，与y轴交于点 $C (0 ， 2)$ .

(1)、求该抛物线的表达式；

(2)、已知 $M (1 ， y_{m})$ ， $N (x_{n} ， y_{n})$ 是抛物线上的两点，根据图象分析，若 $y_{m} \geq y_{n}$ ，则 $x_{n}$ 的取值范围是.

查看试题解析
23. 如图，在 $R t △ A B C$ 中， $∠ A C B = 90 °$ ，点D在 $A B$ 上， $C A = C D$ ，过点B作 $B E ⊥ C D$ ，交 $C D$ 的延长线于点E．

(1)、求证： $△ A B C ∽ △ D B E$ ；

(2)、如果 $B C = 5$ ， $B E = 3$ ，求 $A C$ 的长．

查看试题解析
24. 如图，要测量楼高MN ，在距MN为15m的点B处竖立一根长为5.5m的直杆AB ，恰好使得观测点E ，直杆顶点A和高楼顶点N在同一条直线上.若 $D B = 5 m$ ， $D E = 1.5 m$ ，求楼高MN.

查看试题解析
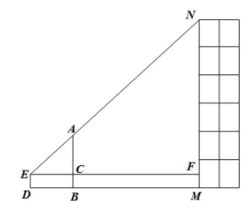25. 2023年8月5日，在成都举行的第31届世界大学生夏季运动会女子篮球金牌赛中，中国队以99比91战胜日本队，夺得冠军.女篮最重要的球员之一韩旭在日常训练中也迎难而上，勇往直前.投篮时篮球以一定速度斜向上抛出，不计空气阻力，在空中划过的运动路线可以看作是抛物线的一部分.建立平面直角坐标系xOy ，篮球从出手到进入篮筐的过程中，它的竖直高度y（单位：m）与水平距离x（单位：m）近似满足二次函数关系，篮筐中心距离地面的竖直高度是3m，韩旭进行了两次投篮训练.

(1)、第一次训练时，韩旭投出的篮球的水平距离x与竖直高度y的几组数据如下：
水平距离x/m
0
1
2
3
4
…
竖直高度y/m
2.0
3.0
3.6
3.8
3.6
…
①在平面直角坐标系xOy中，描出上表中各对对应值为坐标的点，并用平滑的曲线连接；
②结合表中数据或所画图象，直接写出篮球运行的最高点距离地面的竖直高度是 ▲ m；
③已知此时韩旭距篮筐中心的水平距离5m，韩旭第一次投篮练习是否成功，请说明理由.

(2)、第二次训练时，韩旭出手时篮球的竖直高度与第一次训练相同，此时投出的篮球的竖直高度y与水平距离x近似满足函数关系 $y = a {(x - 3)}^{2} + 4.25$ ，若投篮成功，此时韩旭距篮筐中心的水平距离 $d$ 5（填“>”，“=”或“<”）.

查看试题解析
26. 在平面直角坐标系 $x O y$ 中，点 $(1 ， m)$ 和 $(2 ， n)$ 在抛物线 $y = - x^{2} + b x$ 上.

(1)、若 $m = 0$ ，求该抛物线的对称轴；

(2)、若 $m n < 0$ ，设抛物线的对称轴为直线 $x = t$ ，
①直接写出 $t$ 的取值范围；
②已知点 $(- 1 ， y_{1})$ ， $(\frac{3}{2} ， y_{2})$ ， $(3 ， y_{3})$ 在该抛物线上.比较 $y_{1}$ ， $y_{2}$ ， $y_{3}$ 的大小，并说明理由.

查看试题解析
27. 已知等边 $△ A B C$ 中的边长为4，点P ， M分别是边BC ， AC上的一点，以点P为顶点，作 $∠ M P N = 60 °$ ， PN与直线AB交于点N.

(1)、依题意补全图1；

(2)、求证： $B N \cdot C M = C P \cdot B P$

(3)、如图2，若点P为BC中点， $A M = 2 A N$ ，求AN的长.

查看试题解析
28. 如图1，抛物线的顶点为M ，平行于x轴的直线与该抛物线交于点A ， B（点A在点B左侧），根据对称性 $△ A M B$ 恒为等腰三角形，我们规定：当 $△ A M B$ 为直角三角形时，就称 $△ A M B$ 为该抛物线的“完美三角形”.

(1)、①如图2，抛物线 $y = x^{2}$ 的“完美三角形”斜边AB的长为；
②抛物线 $y = x^{2} + 1$ 与 $y = x^{2}$ 的完美三角形的斜边长的数量关系是.

(2)、若抛物线 $y = a x^{2} + 4$ 的“完美三角形”的斜边长为4，求a的值；

(3)、若抛物线 $y = m x^{2} + 2 x + n - 5$ 的“完美三角形”斜边长为n ，且 $y = m x^{2} + 2 x + n - 5$ 的最大值为1，直接写出m ， n的值.

查看试题解析

x	…	-3	-2	-1	0	1	2	n	4	…
y	…	15	m	3	0	-1	0	3	8	…

水平距离x/m	0	1	2	3	4	…
竖直高度y/m	2.0	3.0	3.6	3.8	3.6	…