河北省石家庄市平山县2023-2024学年九年级上学期数学期中考试试卷

试卷更新日期：2023-12-20 类型：期中考试

进入出卷网下载

一、选择题（本大题共16个小题，共38分.1~6小题各3分，7~16小题各2分.在每小题给出的四个选项中，只有一项是符合题目要求的）

1. 点 $(2 ， - 1)$ 关于原点对称的点为（）

A、 $(- 2 ， - 1)$ B、 $(- 2 ， 1)$ C、 $(2 ， 1)$ D、 $(- 1 ， 2)$

查看试题解析
2. 抛物线 $y = x^{2} + 2 x - 1$ 与y轴的交点为（）

A、 $(0 ， - 1)$ B、 $(0 ， 1)$ C、 $(- 1 ， 0)$ D、 $(1 ， 0)$

查看试题解析
3. 一枚质地均匀的正六面体骰子，每个面标有一个数，分别是1，2，3，4，5，6.抛掷这枚骰子1次，朝上一面的数字是5的概率为（）

A、 $\frac{1}{6}$ B、 $\frac{1}{3}$ C、 $\frac{1}{2}$ D、 $\frac{5}{6}$

查看试题解析
4. 在不透明的袋子里装有2个红球、3个白球、2个黑球，它们除颜色外都相同，从袋子中任意摸出1个球.下列判断正确的是（）
甲：摸到红球比摸到白球的可能性小；乙：摸到红球和摸到黑球的可能性相同

A、只有甲对 B、只有乙对 C、甲、乙都对 D、甲、乙都不对

查看试题解析
5. 将抛物线 $y = x^{2} - 1$ 向左平移2个单位长度，再向上平移2个单位长度，所得新抛物线的函数解析式为（）

A、 $y = {(x + 2)}^{2} + 1$ B、 $y = {(x + 2)}^{2} + 2$ C、 $y = {(x + 3)}^{2} + 2$ D、 $y = {(x - 2)}^{2} + 2$

查看试题解析
6. 老师设计了接力游戏，用合作的方式完成配方法解方程，规则：每人只能看到前一人给的方程，并进行一步计算，再将结果传递给下一人，最后解出方程，过程如图所示，接力中，自己负责的一步出现错误的是（）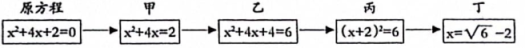

A、只有甲 B、只有丁 C、乙和丁 D、甲和丁

查看试题解析
7. 如图，在平行四边形ABCD中，AC与BD交于点O ，下列说法不一定正确的是（）

A、平行四边形ABCD是中心对称图形 B、将 $△ A B D$ 绕点O旋转 $180 °$ 后可与 $△ C D B$ 重合 C、 $△ O A D$ 与 $△ O C B$ 关于点O对称 D、 $△ A O D$ 绕点O旋转一定角度后可与 $△ D O C$ 重合

查看试题解析
8. 某电影上映的第一天票房约为2亿元，第二、三天单日票房持续增长，三天累计票房6.62亿元.设平均每天票房的增长率为x ，则根据题意，下列方程正确的是（）

A、 $2 + 2 (1 + x) + 2 {(1 + x)}^{2} = 6.62$ B、 $2 {(1 + x)}^{2} = 6.62$ C、 $2 (1 + x) + 2 {(1 + x)}^{2} = 6.62$ D、 $2 x (1 + x) = 6.62$

查看试题解析
9. 如图，在 $△ A B C$ 中， $∠ A B C = 90 °$ ，以边AB的中点O为圆心，OA长为半径作 $⊙ O$ ，交AC于点D ，点E在 $\overset{⌢}{B D}$ 上.若 $∠ A D E = 115 °$ ，则 $∠ E B C$ 的度数为（）

A、 $65 °$ B、 $55 °$ C、 $35 °$ D、 $25 °$

查看试题解析
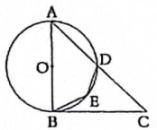10. 二次函数 $y = a x^{2} + b x + c$ 的图象如图所示，下列判断正确的是（）

A、 $a < 0$ B、 $b < 0$ C、当 $x < 1$ 时，y随x的增大而减小 D、 $b^{2} - 4 a c > 0$

查看试题解析
11. 如图， $⊙ O$ 是 $△ A B C$ 的外接圆，D是 $\overset{⌢}{A C}$ 的中点.若 $∠ A B D = 36 °$ ， $⊙ O$ 的半径为5，则 $\overset{⌢}{A C}$ 的长度为（）

A、 $2 π$ B、 $4 π$ C、 $6 π$ D、 $8 π$

查看试题解析
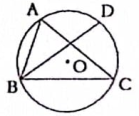12. 为了测量一个铁球的直径，将该铁球放入工件槽（相邻两边互相垂直）内，测得的有关数据如图所示（单位：cm），则该铁球的直径为（）

A、5cm B、8cm C、10cm D、12cm

查看试题解析
13. 定义新运算： $a ★ b = a^{2} - a b + b$ ，例如 $2 ★ 1 = 2^{2} - 2 \times 1 + 1 = 3$ ，则方程 $x ★ 2 = 0$ 的根的情况为（）

A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、无法判断

查看试题解析
14. 某小组做“用频率估计概率”的试验时，统计了某一结果出现的频率，绘制了如图所示的折线统计图，则符合这一结果的试验最有可能的是（）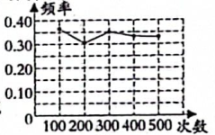

A、掷一枚一元硬币，落地后正面朝上 B、在“石头、剪刀、布”的游戏中，小明随机出的是“剪刀” C、一副去掉大小王的扑克牌洗匀后，从中任抽一张牌的花色是红桃 D、任意写一个整数，它能被2整除

查看试题解析
15. 已知关于x的二次函数 $y = a x^{2} - 6 a x + 9 a + 5 (a < 0)$ ，在 $m \leq x \leq 6$ 的取值范围内，若 $0 < m < 3$ ，则（）

A、函数有最大值 $9 a + 5$ B、函数有最大值5 C、函数没有最小值 D、函数没有最大值

查看试题解析
16. 如图，一个零刻度落在点A的量角器（半圆O），其直径为AB ，一等腰直角三角板MNB绕点B旋转，斜边BN交半圆O于点C ， BM交半圆O于点D ，点C在量角器上的读数为 $α$ .关于结论Ⅰ，Ⅱ，下列判断正确的是（）
结论Ⅰ： $\overset{⌢}{A C} + \overset{⌢}{B D} = \frac{1}{2} \overset{⌢}{A B}$ ；
结论Ⅱ：当边MN与半圆O相切于点E（点E在量角器上的读数为 $β$ ）时， $β - \frac{1}{2} α = 45$

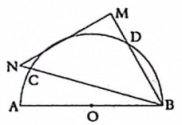A、只有结论Ⅰ对 B、只有结论Ⅱ对 C、结论Ⅰ、Ⅱ都对 D、结论Ⅰ、Ⅱ都不对

查看试题解析

二、填空题（本大题共3个小题，共10分.17小题2分，18~19小题各4分，每空2分）

17. 已知 $⊙ O$ 的直径为8，点P在 $⊙ O$ 内.若OP的长为正整数，写出一个符合条件的OP的长度：.

查看试题解析
18. 如图，在 $△ A B C$ 中， $∠ A B C = 90 °$ ，将 $△ A B C$ 绕点B顺时针旋转 $α (0 ° < α < 90 °)$ 得到 $△ A^{'} B C^{'}$ ， M ， $M^{'}$ 分别为AC ， $A^{'} C^{'}$ 的中点.

(1)、若 $∠ A B C^{'} = 145 °$ ，则 $α =$ 度；

(2)、若 $A C = 10$ ， $M M^{'} = 5$ ，则 $α =$ 度.

查看试题解析
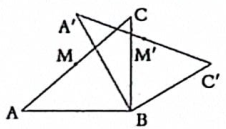19. 如图，嘉嘉用计算机编程模拟抛出的弹跳球落在斜面上反弹后的距离，当弹跳球以某种特定的角度从点 $P (0 ， 1)$ 处抛出后，弹跳球的运动轨迹是抛物线L ，其最高点的坐标为 $(4 ， 5)$ .弹跳球落到斜面上的点A处反弹后，弹跳球的运动轨迹是抛物线 $L^{'}$ ，且开口大小和方向均与L相同，但最大高度只是抛物线L最大高度的 $\frac{2}{5}$ .

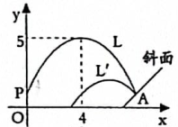(1)、抛物线L的解析式为；

(2)、若点A与点P的高度相同，且点A在抛物线 $L^{'}$ 的对称轴的右侧，抛物线 $L^{'}$ 的对称轴为直线.

查看试题解析

三、解答题（本大题共7个小题，共72分.解答应写出文字说明、证明过程或演算步骤）

20. 在如图所示的方格纸中，每个小方格都是边长为1个单位长度的正方形，图①，图②，图③均为顶点在格点上的三角形（每个小方格的顶点叫格点）.

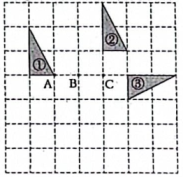(1)、在图中，图①经过变换可以得到图②（填“平移”“旋转”或“轴对称”）；

(2)、在图中画出图①绕点A逆时针旋转 $90 °$ 后得到的图形；

(3)、在图中，图③可由图②经过一次旋转变换得到，其旋转中心是点（填“A”“B”或“C”）.

查看试题解析
21. 老师在黑板上书写了一个正确的演算过程，随后用手掌遮住了一部分，如图所示.

(1)、若所捂的部分为0，求x的值；

(2)、若所捂的部分为 $3 x^{2} - 7 x + 4$ ，求x的值.

查看试题解析
22. 如图，转盘A的三个扇形面积相等，分别标有数字1，2，3，转盘B的四个扇形面积相等，分别标有数字1，2，3，4.转动转盘A ， B各一次，当转盘停止转动时，将指针指向扇形中的两个数字相加（当指针落在两扇形的交线上时，重新转动转盘）.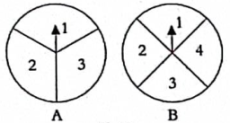

(1)、用树状图列出所有可能出现的结果；

(2)、若规定指针指向扇形中的两个数字的和为5时甲赢，和为4时乙赢，和为其他数字时，甲、乙平局.请问这个游戏对甲、乙两人是否公平？

查看试题解析
23. 如图，正六边形ABCDEF内接于 $⊙ O$ .

(1)、若P是 $\overset{⌢}{C D}$ 上的动点，连接BP ， FP ，求 $∠ B P F$ 的度数；

(2)、已知 $△ A D F$ 的面积为 $2 \sqrt{3}$ .
①求 $∠ D A F$ 的度数；
②求 $⊙ O$ 的半径.

查看试题解析
24. 近年来国家倡导“电动车，上牌照，保安全，戴头盔”.某头盔专卖店购进一批单价为36元的头盔.在销售中，通过分析销售情况发现这种头盔的月销售量y（个）与售价x（元/个）（ $42 \leq x \leq 72$ ）满足函数关系 $y = - 2 x + 200$ .专卖店的优惠活动：若购买一个这种头盔，就赠送一个成本为6元的头盔面罩.

(1)、设专卖店在优惠活动期间，月销售利润为w元，求w与x之间的函数解析式；

(2)、嘉嘉说：“在优惠活动期间，该专卖店的月销售的最大利润能达到1700元.”请判断嘉嘉的说法是否正确，并说明理由.

查看试题解析
25. 如图1，在正方形ABCD中， $A B = 8$ ，点O与点B重合，以点O为圆心，作半径长为5的半圆O ，交AB于点E ，交AB的延长线于点F ，点M ， N是 $\overset{⌢}{E F}$ 的三等分点（点M在点N的左侧）.将半圆O绕点E逆时针旋转，记旋转角为 $α (0 ° < α \leq 90 °)$ ，旋转后，点F的对应点为点 $F^{'}$ .
图1 图2 备用图

(1)、如图2，在旋转过程中，当 $E F^{'}$ 经过点N时.
①求 $α$ 的度数；
②求图中阴影部分的面积；

(2)、在旋转过程中，若半圆O与正方形ABCD的边相切，请直接写出点A到切点的距离.

查看试题解析
26. 如图，抛物线L： $y = a x^{2} - 2 a x + \frac{15}{2} (a \neq 0)$ 与x轴交于 $A (- 3 ， 0)$ ， B两点，与y轴交于点C.

(1)、求抛物线L的解析式和顶点坐标；

(2)、已知点 $Q (m ， \frac{7}{2})$ 在抛物线L上，且到y轴的距离不超过3，求m的值；

(3)、已知点P的坐标为 $(2 ， 2)$ ，连接AP ，坐标平面上放置一透明胶片，并在胶片上描画出抛物线L在x轴上方的一段，记为 $L^{'}$ ，将该胶片向下平移 $d (d \geq 0)$ 个单位长度.
①若平移后的 $L^{'}$ 在x轴上方的部分只有一个整点（横、纵坐标都是整数的点），请直接写出满足条件的整数d的值；
②若平移后的 $L^{'}$ 与线段AP只有一个公共点，求d的取值范围.

查看试题解析