安徽省黄山市休宁县2023-2024学年八年级上学期数学期中考试试卷
试卷更新日期:2023-12-20 类型:期中考试
一、单选题(每小题3分,共30分)
-
1. 下列四个图形中,是轴对称图形的个数是( )
 A、4个 B、3个 C、2个 D、1个2. 正十二边形的一个外角的度数为( )A、30° B、36° C、144° D、150°3. 如图所示,盖房子时,在窗框未安装好之前,木工师傅常常先在窗框上斜钉一根木条,使其窗框不变形,这样做的数学依据是( )
A、4个 B、3个 C、2个 D、1个2. 正十二边形的一个外角的度数为( )A、30° B、36° C、144° D、150°3. 如图所示,盖房子时,在窗框未安装好之前,木工师傅常常先在窗框上斜钉一根木条,使其窗框不变形,这样做的数学依据是( ) A、两点确定一条直线 B、两点之间线段最短 C、三角形的稳定性 D、垂线段最短4. 如图,AC⊥BD于点P,AP=CP,增加下列一个条件:①BP=DP;②AB=CD;③∠A=∠C.其中能判定△ABP≌△CDP的条件有 ( )
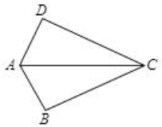
A、两点确定一条直线 B、两点之间线段最短 C、三角形的稳定性 D、垂线段最短4. 如图,AC⊥BD于点P,AP=CP,增加下列一个条件:①BP=DP;②AB=CD;③∠A=∠C.其中能判定△ABP≌△CDP的条件有 ( )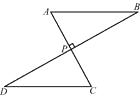 A、0个 B、1个 C、2个 D、3个5. 已知三角形两边的长分别是6和12,则此三角形第三边的长可能是( )A、5 B、6 C、12 D、196. 下列说法正确的是( )A、面积相等的两个三角形全等 B、两边对应相等的两个三角形全等 C、两边一角对应相等的两个三角形全等 D、两角一边对应相等的两个三角形全等7. 如图,内有一点到三个顶点的距离相等,连接、、 , 若 , , 则( )
A、0个 B、1个 C、2个 D、3个5. 已知三角形两边的长分别是6和12,则此三角形第三边的长可能是( )A、5 B、6 C、12 D、196. 下列说法正确的是( )A、面积相等的两个三角形全等 B、两边对应相等的两个三角形全等 C、两边一角对应相等的两个三角形全等 D、两角一边对应相等的两个三角形全等7. 如图,内有一点到三个顶点的距离相等,连接、、 , 若 , , 则( )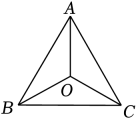 A、 B、 C、 D、8. 如图,AD是△ABC的中线,E是AD上一点,延长BE交AC于F,若BE=AC,BF=9,CF=6,则AF的长度为( )
A、 B、 C、 D、8. 如图,AD是△ABC的中线,E是AD上一点,延长BE交AC于F,若BE=AC,BF=9,CF=6,则AF的长度为( ) A、1 B、1.5 C、2 D、39. 如图所示,有一条直的等宽纸带,按图折叠时形成一个30°的角,则重叠部分的等于( )
A、1 B、1.5 C、2 D、39. 如图所示,有一条直的等宽纸带,按图折叠时形成一个30°的角,则重叠部分的等于( )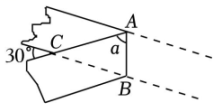 A、75° B、70° C、65° D、60°10. 如图,中, , 的平分线AD与边BC的垂直平分线MD相交于点D , 交AB的延长线于点E , 于点F , 现有下列结论:①;②;③DM平分;④ . 其中正确的有( )
A、75° B、70° C、65° D、60°10. 如图,中, , 的平分线AD与边BC的垂直平分线MD相交于点D , 交AB的延长线于点E , 于点F , 现有下列结论:①;②;③DM平分;④ . 其中正确的有( )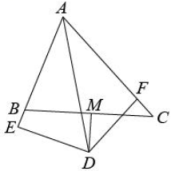 A、①② B、②④ C、①②④ D、①②③④
A、①② B、②④ C、①②④ D、①②③④二、填空题(每小题3分,共24分)
-
11. 如图, , 那么添加条件能根据SAS判定 .
 12. 如图,在中,于点D , 于点E , AD , BE交于点F , , 若 , , 则的面积为 .
12. 如图,在中,于点D , 于点E , AD , BE交于点F , , 若 , , 则的面积为 .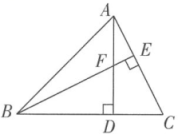 13. 如图,在中,BC的垂直平分线MN交AB于点D , 若 , , 则AC的长度x取值范围为 .
13. 如图,在中,BC的垂直平分线MN交AB于点D , 若 , , 则AC的长度x取值范围为 . 14. 数学在我们的生活中无处不在,就连小小的台球桌上都有数学问题.如图, , 若 , 为了使白球反弹后能将黑球直接撞入袋中,那么击打白球时,必须保证 .
14. 数学在我们的生活中无处不在,就连小小的台球桌上都有数学问题.如图, , 若 , 为了使白球反弹后能将黑球直接撞入袋中,那么击打白球时,必须保证 .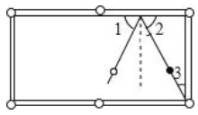 15. 如图, 中, , ,则 的度数是 .
15. 如图, 中, , ,则 的度数是 . 16. 如图,在中, , 的平分线交于点O , D是与平分线的交点,E是的两外角平分线的交点,若 , 则的度数= .
16. 如图,在中, , 的平分线交于点O , D是与平分线的交点,E是的两外角平分线的交点,若 , 则的度数= .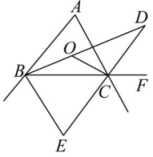 17. 如图,在中, , , , , EF垂直平分BC , 点P为直线EF上的任一点,则的最小值是 .
17. 如图,在中, , , , , EF垂直平分BC , 点P为直线EF上的任一点,则的最小值是 .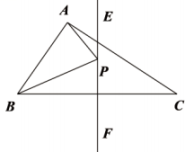 18. 如图,在 ABC 中,AD、CE 是中线,若四边形 BDFE 的面积是 6,则 ABC 的面积为.
18. 如图,在 ABC 中,AD、CE 是中线,若四边形 BDFE 的面积是 6,则 ABC 的面积为.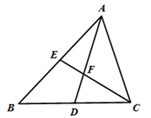
三、解答题(共46分)
-
19. 如图,已知平面直角坐标系中的 , 点
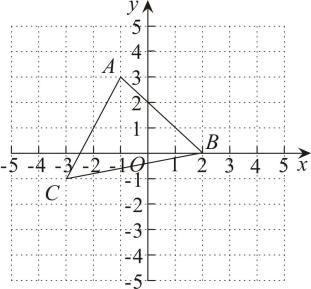 (1)、画出关于x轴的对称图形 , 并写出点A的对应点点的坐标:(2)、求的面积.20. 如图,点E , F在BC上, , , , . 求证: .
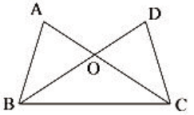
(1)、画出关于x轴的对称图形 , 并写出点A的对应点点的坐标:(2)、求的面积.20. 如图,点E , F在BC上, , , , . 求证: .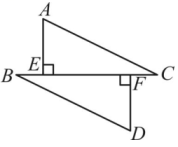 21. 如图,∠A =∠D,OA=OD, ∠DOC=40°,则∠DBC是多少度?
21. 如图,∠A =∠D,OA=OD, ∠DOC=40°,则∠DBC是多少度?
 22. 如图,在平面直角坐标系中,点A的坐标是 , 以线段OA为边向下侧作等边 , 点C为x轴的正半轴上一动点(),连接BC , 以线段BC为边向下侧作等边 , 连接DA并延长,交y轴于点E .
22. 如图,在平面直角坐标系中,点A的坐标是 , 以线段OA为边向下侧作等边 , 点C为x轴的正半轴上一动点(),连接BC , 以线段BC为边向下侧作等边 , 连接DA并延长,交y轴于点E .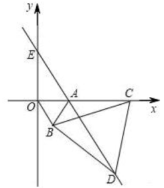 (1)、与全等吗?请说明理由;(2)、当以A , E , C为顶点的三角形是等腰三角形时,求点C的坐标.23. 如图是正三角形,是顶角的等腰三角形,以D为顶点作一个60°角,角的两边分别交AB、AC边于M、N两点,连接MN .
(1)、与全等吗?请说明理由;(2)、当以A , E , C为顶点的三角形是等腰三角形时,求点C的坐标.23. 如图是正三角形,是顶角的等腰三角形,以D为顶点作一个60°角,角的两边分别交AB、AC边于M、N两点,连接MN .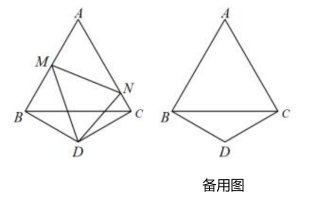 (1)、探究:写出线段BM、MN、NC之间的数量关系,并说明理由.(2)、若点M、N分别是AB、CA延长线上的点,其它条件不变,直接写出线段BM、MN、NC之间的数量关系(不用说明理由),并在图中画出图形.
(1)、探究:写出线段BM、MN、NC之间的数量关系,并说明理由.(2)、若点M、N分别是AB、CA延长线上的点,其它条件不变,直接写出线段BM、MN、NC之间的数量关系(不用说明理由),并在图中画出图形.