安徽省滁州市天长市铜城片2023-2024学年九年级上学期数学期中考试试卷
试卷更新日期:2023-12-20 类型:期中考试
一、选择题(本大题共10小题,每小题4分,满分40分)
-
1. 对于二次函数 , 下列正确的是( )A、有最大值 B、有最小值 C、有最大值 D、有最小值2. 近视眼镜的度数(度)与镜片焦距(m)成反比例,已知200度近视眼镜的镜片焦距为0.5m,若某近视眼镜片的焦距为0.25m,则该眼镜片的度数为( )A、100度 B、300度 C、400度 D、600度3. 若 , 则的值为( )A、2 B、 C、3 D、4. 大自然是美的设计师,即使是一个小小的盆景,经常也会产生最具美感的黄金分割比(黄金分割比约为0.618)。如图,点为的黄金分割点(AB>BC),若cm,则约为( )
 A、42cm B、38cm C、62cm D、70cm5. 如图,在平面直角坐标系中,抛物线与轴交于点 . 过点且与轴平行的直线交抛物线于两点,则的长为( )
A、42cm B、38cm C、62cm D、70cm5. 如图,在平面直角坐标系中,抛物线与轴交于点 . 过点且与轴平行的直线交抛物线于两点,则的长为( ) A、 B、 C、 D、6. 如图,在中,点是线段上一点,连接交于点 , 若 , 则的值为( )
A、 B、 C、 D、6. 如图,在中,点是线段上一点,连接交于点 , 若 , 则的值为( ) A、 B、 C、 D、7. 如图,在中,为上一点, , 则的值为( )
A、 B、 C、 D、7. 如图,在中,为上一点, , 则的值为( ) A、 B、 C、 D、8. 如图,用一根60cm的铁丝制作一个“日”字型框架 , 铁丝恰好全部用完,则该“日”字型框架面积的最大值为( )
A、 B、 C、 D、8. 如图,用一根60cm的铁丝制作一个“日”字型框架 , 铁丝恰好全部用完,则该“日”字型框架面积的最大值为( ) A、150 B、 C、 D、9. 如图,直线与双曲线交于两点,轴于点 , 连接交轴于点。下列结论:①;②的面积为定值;③是的中点;④ . 其中正确的结论有( )
A、150 B、 C、 D、9. 如图,直线与双曲线交于两点,轴于点 , 连接交轴于点。下列结论:①;②的面积为定值;③是的中点;④ . 其中正确的结论有( )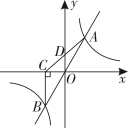 A、1个 B、2个 C、3个 D、4个10. 如图,在中, , , 。有一动点从点出发,以每秒1个单位长度的速度沿折线运动至点时停止.连接 , 设点的运动时间为秒, , 则与之间的函数关系的图象大致是( )
A、1个 B、2个 C、3个 D、4个10. 如图,在中, , , 。有一动点从点出发,以每秒1个单位长度的速度沿折线运动至点时停止.连接 , 设点的运动时间为秒, , 则与之间的函数关系的图象大致是( ) A、
A、 B、
B、 C、
C、 D、
D、
二、填空题(本大题共4小题,每小题5分,满分20分)
-
11. 某零件长是40cm,若该零件在设计图上的长为2mm,则这幅设计图的比例尺为1: .12. 若抛物线与轴两个交点为和 , 当是的值为 .13. 双曲线和如图所示,是双曲线上一点,过点作轴,垂足为 , 交双曲线于点 , 连接 , 若的面积为2,则 .
 14. 如图,矩形的边长 , , 为的中点,点在边上, , 分别与相交于点 .
14. 如图,矩形的边长 , , 为的中点,点在边上, , 分别与相交于点 . (1)、的度数是度;(2)、线段的长为 .
(1)、的度数是度;(2)、线段的长为 .三、(本大题共2小题,每小题8分,满分16分)
-
15. 已知二次函数经过点 , , 求二次函数的表达式,并判断该二次函数的图象与轴有几个交点.16. 如图所示是反比例函数的图象的一支。根据图象回答下列问题:
 (1)、图象的另一支在哪个象限?常数的取值范围是什么?(2)、在这个函数图象的某一支上任取两点 , , 如果 , 试比较和的大小.
(1)、图象的另一支在哪个象限?常数的取值范围是什么?(2)、在这个函数图象的某一支上任取两点 , , 如果 , 试比较和的大小.四、(本大题共2小题,每小题8分,满分16分)
-
17. 在的网格中,已知和点 .
 (1)、以点为位似中心,画出的位似图形 , 使其与的相似比为2;(2)、写出各顶点的坐标.18. 如图,已知 , , .
(1)、以点为位似中心,画出的位似图形 , 使其与的相似比为2;(2)、写出各顶点的坐标.18. 如图,已知 , , . (1)、求的长;(2)、求的长.
(1)、求的长;(2)、求的长.五、(本大题共2小题,每小题10分,满分20分)
-
19. 如图,抛物线与直线交于两点(点在点的左侧).
 (1)、求两点的坐标;(2)、设抛物线的顶点为 , 连接 , 试求的面积.20. 如图,在中, , . 分别在上,且 , 若 , .
(1)、求两点的坐标;(2)、设抛物线的顶点为 , 连接 , 试求的面积.20. 如图,在中, , . 分别在上,且 , 若 , . (1)、求证:;(2)、求的长.
(1)、求证:;(2)、求的长.六、
-
21. 如图,在平面直角坐标系中,矩形的顶点在轴上,顶点在第一象限.反比例函数的图象经过点交与点 , .
 (1)、求的值;(2)、若点恰好为的中点.
(1)、求的值;(2)、若点恰好为的中点.①求直线的表达式;
②请根据图象直接写出在第一象限内,当取何值时,反比例函数的函数值小于直线对应函数的函数值.
七、(本题满分12分)
-
22. 在一次足球训练中,小明从球门正前方8m的处射门,球射向球门的路线呈抛物线,当球飞行的水平距离为6m时,球达到最高点,此时球离底面3m.已知球门高为2.44m,现以为原点,建立如图所示直角坐标系.
 (1)、求抛物线的表达式;(2)、通过计算判断球能否进球门;(3)、若抛物线的形状、最大高度均保持不变,且抛物线恰好经过点正上方2.25m处,则该抛物线应向右平移几个单位?
(1)、求抛物线的表达式;(2)、通过计算判断球能否进球门;(3)、若抛物线的形状、最大高度均保持不变,且抛物线恰好经过点正上方2.25m处,则该抛物线应向右平移几个单位?八、(本题满分14分)
-
23. 如图,四边形为边长为2的正方形,且是边延长线上一点,过点作于点 , 交于点 , 交于点 .
 (1)、求证:;(2)、若是的中点,求的值;(3)、连接 , 求的度数.
(1)、求证:;(2)、若是的中点,求的值;(3)、连接 , 求的度数.
-
-