河北省张家口市桥西区2023-2024学年九年级上学期期中数学试卷

试卷更新日期：2023-12-20 类型：期中考试

进入出卷网下载

一、选择题（本大题共16个小题，共38分．1～6小题各3分，7～16小题各2分．在每小题给出的四个选项中，只有一项是符合题目要求的）

1. 下列函数中，是二次函数的是（　　）

A、y＝2x﹣1 B、y＝2x²﹣1 C、2x²＝1 D、 $y = \frac{2}{x}$

查看试题解析
2. 若 $\frac{a}{2} = \frac{3}{b}$ ，则 $a b =$ （）

A、6 B、 $\frac{3}{2}$ C、1 D、 $\frac{2}{3}$

查看试题解析
3. 下列是描述小明和小颖在同一盏路灯下影子的图片，其中合理的是（）

A、 B、 C、 D、

查看试题解析
4. 若两个相似三角形周长的比为 $1 ： 4$ ，则这两个三角形对应边的比是（）

A、 $1 ： 2$ B、 $1 ： 4$ C、 $1 ： 8$ D、 $1 ： 16$

查看试题解析
5. 反比例函数 $y = - \frac{6}{x}$ 的图象一定不经过的点是（　　）

A、（﹣3，﹣2） B、（2，3） C、（2，﹣3） D、（﹣2，﹣4）

查看试题解析
6. 在△ABC中，∠A、∠B、∠C的对边分别为a、b、c ．已知a＝5，b＝12，c＝13，则tan∠A的值为（　　）

A、 $\frac{5}{13}$ B、 $\frac{12}{13}$ C、 $\frac{12}{5}$ D、 $\frac{5}{12}$

查看试题解析
7. 如图的立体图形由相同大小的正方体积木堆叠而成．判断拿走图中的哪一个积木后，此图形前视图的形状会改变（　　）

A、甲 B、乙 C、丙 D、丁

查看试题解析
8. 一元二次方程x²+5＝4x根的情况为（　　）

A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、不能判定

查看试题解析
9. 如图，四边形ABCD是菱形，对角线AC与BD相交于点O ， AB＝5，AO＝4，则BD等于（　　）

A、4 B、5 C、6 D、7

查看试题解析
10. 用配方法解方程x²﹣4x﹣1＝0时，配方后正确的是（　　）

A、（x+2）²＝3 B、（x+2）²＝17 C、（x﹣2）²＝5 D、（x﹣2）²＝17

查看试题解析
11. 如图，将四根木条用钉子钉成一个矩形框架 $A B C D$ ，然后向左扭动框架，观察所得四边形的变化．下面判断错误的是（）

A、四边形 $A B C D$ 由矩形变为平行四边形 B、对角线 $B D$ 的长度减小 C、四边形 $A B C D$ 的面积不变 D、四边形 $A B C D$ 的周长不变

查看试题解析
12. 已知压力F（N）、压强P（Pa）与受力面积S（m²）之间有如下关系式：F＝PS ．当F为定值时，如图中大致表示压强P与受力面积S之间函数关系的是（　　）

A、 B、 C、 D、

查看试题解析

13. 小明按照以下步骤画线段AB的三等分点：

画法

图形

1．以A为端点画一条射线；

2．用圆规在射线上依次截取3条等长线段AC、CD、DE ，连接BE；

3．过点C、D分别画BE的平行线，交线段AB于点M、N ， M、N就是线段AB的三等分点．

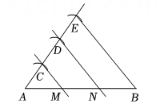
这一画图过程体现的数学依据是（）

A、两直线平行，同位角相等 B、两条平行线之间的距离处处相等 C、垂直于同一条直线的两条直线平行 D、两条直线被一组平行线所截，所得的对应线段成比例

查看试题解析

14. 利用公式解可得一元二次方程式2x²﹣9x+8＝0的两解为a、b ，且a＞b ，则a的值为（　　）

A、 $\frac{9 + \sqrt{17}}{4}$ B、 $\frac{9 - \sqrt{17}}{4}$ C、 $\frac{- 9 + \sqrt{17}}{4}$ D、 $\frac{- 9 - \sqrt{17}}{4}$

查看试题解析
15. 如图1，在Rt△ABC中，∠ABC＝90°，AB＝8，BC＝6，D是AB上一点，且AD＝2，过点D作DE∥BC交AC于E ，将△ADE绕A点顺时针旋转到图2的位置．则图2中 $\frac{B D}{C E}$ 的值为（　　）

A、 $\frac{3}{5}$ B、 $\frac{4}{5}$ C、 $\frac{4}{3}$ D、 $\frac{3}{4}$

查看试题解析
16. 抛物线y＝ax²﹣a（a≠0）与直线y＝kx交于A（x₁ ， y₁），B（x₂ ， y₂）两点，若x₁+x₂＜0，则关于直线y＝ax+k；甲答：一定经过一、四象限，乙答：一定经过一、三象限．则正确的是（　　）

A、甲乙均错 B、甲乙均对 C、甲错乙对 D、甲对乙错

查看试题解析

二、填空题（本大题共3个小题，共10分，17小题2分；18-19小题各4分，每空2分）

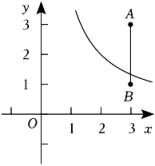
17. 如图，已知点A（3，3），B（3，1），反比例函数 $y = \frac{k}{x} (k \neq 0)$ 图象的一支与线段AB有交点，写出一个符合条件的k的整数值：．

查看试题解析
18. 一个盒子里装有10个红球和若干个白球，这些球除颜色外其余都相同．几名同学轮流从盒子里摸1个球，记录下所摸球的颜色后，再把球放回盒子里搅匀，记录如下：
摸球次数
20
40
60
80
100
120
140
160
180
200
220
240
出现红球的频数
11
23
33
38
49
59
69
81
91
101
109
121
根据以上表格可估计摸到红球的概率为（结果保留小数点后一位），袋中白球约有个．

查看试题解析
19. 如图，折叠矩形ABCD的一边AD ，使D落在BC边上的F处，且 $t a n ∠ E F C = \frac{3}{4}$ ．
⑴△AFB与△FEC是否相似？（选填“是”或者“否”）．
⑵若 $A E = 5 \sqrt{5} c m$ 则矩形ABCD的面积为 cm² ．

查看试题解析

三、解答题（本大题共7个小题，共52分，解答应写出文字说明、证明过程或演算步骤）

20. 计算：tan30°﹣2sin60°．

查看试题解析
21. 有三张大小一样而画面不同的画片，先将每一张从中间剪开，分成上下两部分；然后把三张画片的上半部分都放在第一个盒子中，把下半部分都放在第二个盒子中．分别摇匀后，从每个盒子中各随机地摸出一张，求这两张恰好能拼成原来的一幅画的概率．

查看试题解析
22. 教室里的投影仪投影时，可以把投影光线CA ， CB及在黑板上的投影图象高度AB抽象成如图所示的△ABC ， ∠BAC＝90°，黑板上投影图象的高度AB＝120cm ， CB与AB的夹角∠B＝33.7°，求AC的长．（结果精确到1cm ．参考数据：sin33.7°≈0.55，cos33.7°≈0.83，tan33.7°≈0.67）

查看试题解析
23. 为了便于劳动课程的开展，学校打算建一个矩形生态园 $A B C D$ （如图），生态园一面靠墙（墙足够长），另外三面用 $18 m$ 的篱笆围成．生态园的面积能否为 $40 m^{2}$ ？如果能，请求出 $A B$ 的长；如果不能，请说明理由．

查看试题解析
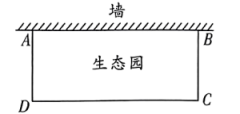24. 如图，矩形ABCD中，过对角线BD的中点O作BD的垂线EF ，分别交AD ， BC于点E ， F ．判断四边形EBFD的形状，并说明理由．

查看试题解析
25. 在平面直角坐标系xOy中，抛物线y＝ax²﹣4a（a≠0）与x轴的交点为A、B ，（点A在点B的左侧），顶点为C ．

(1)、求AB的长；

(2)、若以A、B、C为顶点的三角形为直角三角形，求a的值；

(3)、横、纵坐标都是整数的点叫做整点，若抛物线在点A ， B之间的部分与线段AB所围成的区域内（不包括边界）恰有1个整点，结合函数的图象，直接写出a的取值范围．

查看试题解析
26. 如图1，在三角形ABC中，角ACB＝90度，AC＝6cm ， BC＝8cm ，动点P从点B出发，在BA边上以每秒5cm的速度向点A匀速运动，同时动点Q从点C出发，在CB边上以每秒4cm的速度向点B匀速运动，运动时间为t秒，连接PQ ．

(1)、若三角形BPQ与三角形ABC相似，求t的值；

(2)、直接写出三角形BPQ是等腰三角形时t的值；

(3)、如图2，连接AQ、CP ，若AQ垂直CP ，求t的值．

查看试题解析

摸球次数	20	40	60	80	100	120	140	160	180	200	220	240
出现红球的频数	11	23	33	38	49	59	69	81	91	101	109	121