安徽省宣城市2023-2024学年八年级上学期数学期中考试试卷
试卷更新日期:2023-12-20 类型:期中考试
一、选择题(本大题共10小题,共30分。在每小题列出的选项中,选出符合题目的一项)
-
1. 在平面直角坐标系中,点所在象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限2. 一次函数的图象不经过( )A、第一象限 B、第二象限 C、第三象限 D、第四象限3. 下列说法错误的是( )
A、三角形的中线、高、角平分线都是线段 B、任意三角形内角和都是180° C、三角形按角可分为锐角三角形、直角三角形和等腰三角形 D、直角三角形两锐角互余4. 直线上有两点 , , 且 , 则与的大小关系是( )A、 B、 C、 D、无法确定5. 若一个三角形的两边长分别为5和8,则第三边长可能是( )A、2 B、3 C、10 D、146. 下列命题中,为真命题的是( )A、两个锐角之和一定为钝角 B、相等的两个角是对顶角 C、同位角相等 D、垂线段最短7. 在中, , 则是( )A、锐角三角形 B、直角三角形 C、钝角三角形 D、等腰直角三角形8. 一次函数与正比例函数(k , b为常数,且)在同一平面直角坐标系中的图象可能是( )A、 B、
B、 C、
C、 D、
D、 9. 如图,将一张三角形纸片的一角折叠,使点A落在外的处,折痕为.如果 , , , 那么下列式子中正确的是( )
9. 如图,将一张三角形纸片的一角折叠,使点A落在外的处,折痕为.如果 , , , 那么下列式子中正确的是( ) A、 B、 C、 D、10. 在平面直角坐标系中,已知A , B , C , D四点的坐标依次为 , , , , 若一次函数()图象将四边形的面积分成1∶3两部分,则m的值为( )A、-4 B、 , -4 C、 D、 , -5
A、 B、 C、 D、10. 在平面直角坐标系中,已知A , B , C , D四点的坐标依次为 , , , , 若一次函数()图象将四边形的面积分成1∶3两部分,则m的值为( )A、-4 B、 , -4 C、 D、 , -5二、填空题(本大题共8小题,共24分)
-
11. 在平面直角坐标系中,点到x轴的距离是.12. 一个三角形的两边长分别是3和8,周长是偶数,那么第三边边长是.13.
如图,把一副常用的三角板如图所示拼在一起,那么图中∠ABF= .
 14. 函数是正比例函数,则.15. 与直线垂直且过点的直线解析式是.16. 在平面直角坐标系中,当不是坐标轴上点时,定义M的“影子点”为 , 点的“影子点”是点 , 则点的“影子点”的坐标为.17. 已知一次函数 , 无论k取任意实数,则该一次函数的图象必经过点.18. 如图,长方形各边分别平行于x轴或y轴,甲、乙两点由处同时出发,沿长方形的边作环绕运动,甲点按逆时针方向以1个单位/秒匀速运动,乙点按顺时针方向以2个单位/秒匀速运动,则两点出发后第2023次相遇点的坐标是.
14. 函数是正比例函数,则.15. 与直线垂直且过点的直线解析式是.16. 在平面直角坐标系中,当不是坐标轴上点时,定义M的“影子点”为 , 点的“影子点”是点 , 则点的“影子点”的坐标为.17. 已知一次函数 , 无论k取任意实数,则该一次函数的图象必经过点.18. 如图,长方形各边分别平行于x轴或y轴,甲、乙两点由处同时出发,沿长方形的边作环绕运动,甲点按逆时针方向以1个单位/秒匀速运动,乙点按顺时针方向以2个单位/秒匀速运动,则两点出发后第2023次相遇点的坐标是.
三、解答题(本大题共8小题,共46分。解答应写出文字说明,证明过程或演算步骤)
-
19. 已知一次函数的图象经过点和 , 求这个一次函数的解析式.20. 已知在平面直角坐标系中的位置如图所示.将向右平移6个单位长度,再向下平移6个单位长度得到.(图中每个小方格边长均为1个单位长度).
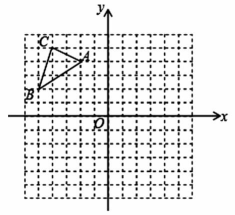 (1)、在图中画出平移后的;(2)、直接写出各顶点的坐标.
(1)、在图中画出平移后的;(2)、直接写出各顶点的坐标.;;.
21. 已知与成正比例,且时,.(1)、求y与x之间的函数关系式;(2)、点在这个函数的图象上吗?22. 如图,在中,E是中线的中点,的面积是1,求的面积. 23. 中,点D , E在边上,平分 , , , , 求的度数.
23. 中,点D , E在边上,平分 , , , , 求的度数. 24. A、B两地相距300千米,甲、乙两车先后从A地出发到B地.如图,线段表示甲车离A地距离y(千米)与时间x(小时)之间的函数关系;折线表示乙车离A地距离y(千米)与x(小时)之间的函数关系.根据图象回答下列问题.
24. A、B两地相距300千米,甲、乙两车先后从A地出发到B地.如图,线段表示甲车离A地距离y(千米)与时间x(小时)之间的函数关系;折线表示乙车离A地距离y(千米)与x(小时)之间的函数关系.根据图象回答下列问题. (1)、直接写出线段EF对应的函数解析式;(2)、求点P的坐标,并说出点P坐标的实际意义.25. 在平面直角坐标系 中,一次函数 的图象由函数 的图象向下平移1个单位长度得到.(1)、求这个一次函数的解析式;(2)、当 时,对于 的每一个值,函数 的值大于一次函数 的值,直接写出 的取值范围.26. 综合与探究:
(1)、直接写出线段EF对应的函数解析式;(2)、求点P的坐标,并说出点P坐标的实际意义.25. 在平面直角坐标系 中,一次函数 的图象由函数 的图象向下平移1个单位长度得到.(1)、求这个一次函数的解析式;(2)、当 时,对于 的每一个值,函数 的值大于一次函数 的值,直接写出 的取值范围.26. 综合与探究:如图1,平面直角坐标系中,一次函数的图象分别交x轴、y轴于点A , B , 一次函数的图象经过点A , 并与y轴交于点C.
 (1)、写出A , B两点的坐标及k的值;(2)、如图2,若点P是x轴正半轴上的一个动点,过点P作轴x的垂线,分别交直线 , 于点M , N.设点P的横坐标为m().
(1)、写出A , B两点的坐标及k的值;(2)、如图2,若点P是x轴正半轴上的一个动点,过点P作轴x的垂线,分别交直线 , 于点M , N.设点P的横坐标为m().①当点P在线段上时,用含m的代数式表示线段的长为 ;
②作点M关于x轴的对称点 , 在点P运动过程中,当时,求点P的坐标.