安徽省六安市霍邱县2023-2024学年八年级上学期数学期中考试试卷

试卷更新日期：2023-12-20 类型：期中考试

进入出卷网下载

一、选择题（本大题共有10小题，每小题4分，共计40分）

1. 下列长度的三条线段能组成三角形的是（）

A、1，1，2 B、2，3，6 C、3，4，7 D、6，8，9

查看试题解析
2. 已知点A在第三象限，到x轴的距离为3，到y轴的距离为4，则点A的坐标为（）

A、 $(3 ， 4)$ B、 $(- 3 ， 4)$ C、 $(- 4 ， - 3)$ D、 $(- 3 ， - 4)$

查看试题解析
3. 下列图像中不能表示y是x的函数的是（）

A、 B、 C、 D、

查看试题解析
4. 妈妈从家里出发去公园锻炼，她连续匀速走了 $50 m i n$ 后回到家，如图，图中的折线段 $O A - A B - B C$ 是她出发后所在位置离家的距离 $s (k m)$ 与行走时间 $t (m i n)$ 之间的关系，则下列图形中可以大致描述妈妈行走的路线的是（）

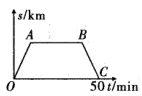A、 B、 C、 D、

查看试题解析
5. 已知函数 $y = (k - 1) x + b - 1$ 是关于x的正比例函数，则关于字母k、b的取值正确的是（）

A、 $k \neq 1$ ， $b = 1$ B、 $k = 1$ ， $b = - 1$ C、 $k = 1$ ， $b \neq 1$ D、 $k \neq 1$ ， $b = - 1$

查看试题解析
6. 对于函数 $y = - x + 1$ ，下列结论正确的是（）

A、它的图象必经过点 $(- 1 ， 0)$ B、它的图象经过第一、二、三象限 C、当 $x > 1$ 时， $y < 0$ D、y的值随x值的增大而增大

查看试题解析
7. 如图，在 $△ A B C$ 中，已知点D、E、F分别是 $B C$ 、 $A D$ 、 $C E$ 的中点，且 $S_{△ A B C} = 4$ ，则 $S_{△ B E F}$ 为（）

A、2 B、1 C、 $\frac{1}{2}$ D、 $\frac{1}{4}$

查看试题解析
8. 一次函数 $y_{1} = k x + b$ 与 $y_{2} = x + a$ 的图象如图所示，则下列结论：① $k < 0$ ；② $a > 0$ ；③关于x的方程 $k x - x = a - b$ 的解是 $x = 3$ ；④当 $x < 3$ 时， $y_{1} < y_{2}$ 中，正确的序号有（）

A、①② B、①③ C、②④ D、③④

查看试题解析
9. 2023年杭州亚运会竞赛项目中，有一个中华民族传统运动项目一一赛龙舟，此项比赛共分为六个小项目，中国健儿成绩骄人，共获得五金一银.在500米直道竞速赛道上，甲、乙两队所划行的路程y（单位：米）与时间t（单位：分）之间的函数关系如图所示，根据图中提供的信息，有下列说法：①甲队比乙队提前0.5分钟到达终点；②当划行1分钟时，甲队比乙队落后50米；③当划行 $\frac{5}{3}$ 分钟时，甲队追上乙队；④当甲队追上乙队时，两队划行的路程都是300米.其中错误的是（）

A、① B、② C、③ D、④

查看试题解析
10. 在平面直角坐标系中，已知两直线 $y = k x + k (k \neq 0)$ 与 $y = 3 x - 6$ 相交于第四象限，则k的取值范围是（）

A、 $- 6 < k < 0$ B、 $- 3 < k < 0$ C、 $- 6 < k < - 3$ D、 $k < - 6$

查看试题解析

二、填空题（本大题共有4小题，每小题5分，共计20分）

11. 围棋起源于中国，它蕴含着中华文化的丰富内涵，是中国文化与文明的体现.如图，围棋盘放在某个平面直角坐标系内，黑棋①的坐标为 $(- 1 ， - 2)$ ，白棋④的坐标为 $(- 4 ， - 3)$ ，则白棋②的坐标为.

查看试题解析
12. 如图，三角形有一部分被墨迹所遮挡，观察可判断三角形的形状为三角形.（填“锐角”、“直角”或“钝角”）

查看试题解析
13. 若将直线 $y = 2 x + 3$ 平移，使其经过点 $(1 ， - 1)$ ，则平移后所得的直线表达式为.

查看试题解析
14. 已知关于x的两个一次函数 $y_{1} = a x - a + 1$ ， $y_{2} = k x + 2 k - 4$ （其中k ， a均为常数）.

(1)、若两个一次函数的图象都经过y轴上的同一个点，则 $a + 2 k =$ ；

(2)、若对于任意实数x ， $y_{1} > y_{2}$ 都成立，则k的取值范围是.

查看试题解析

三、解答题（本大题共有9小题，共计90分）

15. 已知平面直角坐标系中有一点 $M (m - 1 ， 2 m + 3)$ .

(1)、点M在x轴上，求M的坐标；

(2)、当点 $N (5 ， - 1)$ 且 $M N / / x$ 轴时，求M的坐标.

查看试题解析
16. 已知A、B两地相距 $30 k m$ ，小明以 $6 k m / h$ 的速度从A步行到B地，若设他到B地的距离为 $y k m$ ，步行的时间为 $x h$ .

(1)、求y与x之间的函数表达式，并指出y是x的什么函数；

(2)、写出该函数自变量的取值范围.

查看试题解析
17. 如图，在平面直角坐标系中， $△ A B C$ 的顶点坐标分别为 $A (- 2 ， 4)$ ， $B (- 5 ， - 1)$ ， $C (0 ， 1)$ ，把 $△ A B C$ 进行平移，平移后得到 $△ A_{1} B_{1} C_{1}$ ，且 $△ A B C$ 内任意点 $P (x ， y)$ 平移后的对应点为 $P_{1} (x + 3 ， y - 4)$ .

(1)、画出平移后的图形；

(2)、计算 $△ A B C$ 的面积.

查看试题解析
18. 已知y与 $x + 1$ 成正比例，且当 $x = 1$ 时， $y = 6$ .

(1)、求出y与x之间的函数表达式；

(2)、当 $- 3 \leq y \leq 5$ 时，求x的最大值.

查看试题解析
19. 如图，在 $△ A B C$ 中， $∠ A = 28 °$ ， $∠ A B C = 120 °$ ， $C D$ 是 $△ A B C$ 的角平分线.

(1)、线段 $C E$ 是 $A B$ 边上的高线，请在图中画出 $C E$ ；

(2)、在（1）条件下，求 $∠ D C E$ 的度数.

查看试题解析
20. 在平面直角坐标系中，一只蚂蚁从原点O出发，按向上、向右、向下、向右的方向依次不断地移动，每次移动1个单位长度.其行走路线如图所示.

(1)、填写下列各点的坐标： $A_{4} (____，____)$ ， $A_{10} (____，____)$ ， $A_{15} (____，____)$ ；

(2)、写出点 $A_{2023}$ 的坐标；

(3)、指出蚂蚁从点 $A_{2022}$ 到点 $A_{2023}$ 的移动方向.

查看试题解析
21. 如图：已知直线 $y = k x + b$ 经过点 $A (5 ， 0)$ 、 $B (1 ， 4)$ .

(1)、求直线 $A B$ 所对应的函数表达式；

(2)、求直线 $y = 2 x - 4$ 与直线 $A B$ 相交于点C ，求点C的坐标；

(3)、根据图象，直接写出关于x的不等式 $2 x - 4 > k x + b > 0$ 的解集.

查看试题解析
22. 习近平总书记说：“人民群众多读书，我们的民族精神就会厚重起来、深邃起来．”某书店计划在4月23日世界读书日之前，同时购进A，B两类图书，已知A类图书每本的进价36元，B类图书每本的进价45元．

(1)、该书店计划用4500元全部购进两类图书，设购进A类x本，B类y本．求y关于x的关系式；

(2)、进货时，A类图书的购进数量不少于60本，已知A类图书每本的售价为38元，B类图书每本的售价为50元，若书店全部售完可获利W元，求W关于x的关系式，并说明应该如何进货才能使书店所获利润最大，最大利润为多少元？

查看试题解析
23. 小颖根据学习函数的经验，对函数 $y = 1 - | x - 1 |$ 的图象与性质进行了探究，下面是小颖的探究过程，请你补充完整.

(1)、列表：
请把列表补充完整并在所给坐标系中画出该函数的图象；
x
…
$- 2$
$- 1$
0
1
2
3
4
…
y
…
$- 2$
1
0
$- 1$
…

(2)、根据函数图象解决问题：
①该函数的最大值为；
②若y随x的增大而减小，则x应满足的条件是；

(3)、运用合适的方法探究：若在同一坐标系中另有一次函数 $y_{1} = \frac{1}{2} x - 1$ ，
①当 $y_{1} < y$ 时，x的取值范围是；
②将 $y_{1} = \frac{1}{2} x - 1$ 沿y轴怎样平移？能使 $y_{1}$ 与y的函数图象无交点？请写出具体的平移方向和距离.

查看试题解析

x	…	$- 2$	$- 1$	0	1	2	3	4	…
y	…	$- 2$			1	0	$- 1$		…