河北省邯郸市永年区2023-2024学年七年级上学期期中考试数学试题

试卷更新日期：2023-12-20 类型：期中考试

进入出卷网下载

一、选择题（16个小题，每题3分，共48分。在每小题给出的四个选项中，只有一项是符合题目要求的）

1. 下列实物图中，能抽象出圆柱体的是（）

A、 B、 C、 D、

查看试题解析
2. 一艘潜水艇静止在海平面下100米处记作0米．这时如果潜水艇上浮60米记作 $+ 60$ 米，那么潜水艇下沉60米可以用下面直线上的（）点来表示.

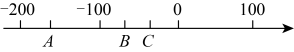A、A B、B C、C D、无法解答

查看试题解析
3. 如图，已知四条线段 $a$ ， $b$ ， $c$ ， $d$ 中的一条与挡板另一侧的线段n在同一直线上，请借助直尺判断该线段是（）

A、 $a$ B、 $b$ C、 $c$ D、 $d$

查看试题解析
4. 如图，将一刻度尺放在数轴上（数轴的单位长度是 $1 c m$ ），刻度尺上“ $0 c m$ ”和“ $3 c m$ ”分别对应数轴上的3和0，那么刻度尺上“ $5.6 c m$ ”对应数轴上的数为（）

A、 $- 5.6$ B、 $- 2.4$ C、 $- 6.5$ D、 $- 2.6$

查看试题解析
5. $- 3$ 的相反数是（）

A、 $- 3$ B、3 C、 $- \frac{1}{3}$ D、 $\frac{1}{3}$

查看试题解析
6. 如图，B、C、D三点在直线l上，点A在直线l外，下列说法正确的是（）

A、直线 $B D$ 和直线 $C D$ 表示的是同一条直线 B、射线 $B D$ 和射线 $C D$ 表示的是同一条射线 C、 $∠ A$ 和 $∠ B A D$ 表示的是同一个角 D、 $∠ 1$ 和 $∠ B$ 表示的是同一个角

查看试题解析
7. 若用我们数学课本上采用的科学计算器按顺序输入：
表示的计算式正确的是（）

A、 $- 4^{2} - \frac{5}{6}$ B、 ${(- 4)}^{2} - \frac{5}{6}$ C、 $- 4^{2} - \frac{6}{5}$ D、 ${(- 4)}^{2} - 5 \times 6$

查看试题解析
8. 下列大小比较正确的是（）

A、 $- 5 > 1$ B、 $- 9.1 > - | - 9.01 |$ C、 $- \frac{6}{7} > - \frac{5}{6}$ D、 $0 > - 100$

查看试题解析
9. 下列各式中，正确的是（）

A、 $35.5 ° = 35 ° 5 0^{'}$ B、 $15 ° 1 2^{'} 3 6^{″} = 15.48 °$ C、 $28 ° 1 8^{'} 1 8^{″} = 28.33 °$ D、 $65.25 ° = 65 ° 1 5^{'}$

查看试题解析
10. 下列说法正确的是（）

A、 $- 2^{5}$ 的底数是 $- 2$ B、 $2^{5}$ 表示5个2相加 C、 $- \frac{2_{}^{3}}{3}$ 的底数是2 D、 $(- 3)^{3}$ 与 $- 3^{3}$ 意义相同

查看试题解析
11. 如图，把三角形 $A B C$ 绕点C顺时针旋转 $35 °$ ，得到三角形 $A^{'} B^{'} C$ ．若 $∠ A^{'} C B = 105 °$ ，则 $∠ A C B^{'}$ 的度数为（）

A、 $30 °$ B、 $35 °$ C、 $45 °$ D、 $70 °$

查看试题解析
12. 下列结果相等的是（）

A、 $1 \div (\frac{1}{2} - \frac{1}{3})$ 与 $1 \times 2 - 1 \times 3$ B、 $| - 1 |$ 与 $- (+ 1)$ C、 $(- 3)^{2}$ 和 $- (- 3^{2})$ D、 $2 \div 3 \times \frac{1}{3}$ 与 $- 4 + 6$

查看试题解析
13. 小明将一副三角板摆成如图形状，下列结论不一定正确的是（）

A、 $∠ C O A = ∠ D O B$ B、 $∠ C O A$ 与 $∠ D O A$ 互余 C、 $∠ A O D = ∠ B$ D、 $∠ A O D$ 与 $∠ C O B$ 互补

查看试题解析
14. 若计算式子（2□7）△ $(- \frac{1}{3})$ 的结果为最大，则应分别在□，△中填入下列选项中的（）

A、+，- B、×，- C、÷，- D、-，÷

查看试题解析
15. 如图， $A 、 B 、 C 、 D$ 是直线上的顺次四点， $M 、 N$ 分别是 $A B 、 C D$ 的中点，且 $M N = 6 c m ， B C = 3 c m$ ，则 $A D$ 的长等于（）．

A、 $8 c m$ B、 $9 c m$ C、 $10 c m$ D、 $11 c m$

查看试题解析
16. 下图是一个数值转换机的示意图，若输入x的值为3，y的值为 $- 2$ 时，则输出的结果为（）

A、5 B、2 C、1 D、6

查看试题解析

二、填空题（三个小题，其中17-18每题3分，19题4分，共10分）

17. 已知 $∠ 1$ 和 $∠ 2$ 互为余角，且 $∠ 2$ 与 $∠ 3$ 互补， $∠ 1 = 60 ° 1 5^{'}$ ，则 $∠ 3$ 的度数为.

查看试题解析
18. 若 $| x | = 2$ ， $| y | = 4$ ，且 $x y < 0$ ，则 $x + y$ =.

查看试题解析
19. 有一题目：“已知 $∠ A O B = 80 °$ ， $∠ B O C = 30 °$ ， $O M$ 平分 $∠ A O B$ ，求 $∠ C O M$ 的度数．”嘉嘉的解答过程为：如图， $∠ B O M = \frac{1}{2} ∠ A O B = 40 °$ ， $∠ C O M = ∠ B O M - ∠ B O C = 10 °$ ．而淇淇说：“嘉嘉考虑的不周全， $∠ C O M$ 还应有另一个不同的值．”
甲、乙、丙、丁四位同学对嘉嘉和淇淇的评论如下：
甲：淇淇说的对，且 $∠ C O M$ 的另一个值是 $70 °$ .
乙：淇淇说的不对， $∠ C O M$ 就是 $10 °$ .
丙：嘉嘉求的结果不对， $∠ C O M$ 应得 $15 °$ .
丁：两人都不对， $∠ C O M$ 应有3个不同的值.
那么你认为 $∠ C O M$ 的值有个，度数为.

查看试题解析

三、解答题（7道题，共62分。解答应写出文字说明、证明过程或演算步骤）

20. 把下列各数分类：
$- 3.14$ ， $4.3$ ， $+ 72$ ， $0$ ， $\frac{1}{3}$ ， $- 6$ ， $- 7.3$ ， $- 12$ ， $0.4$ ， $- \frac{5}{6}$ ， $\frac{22}{7}$ ， $26$ ．

(1)、正整数：{ }；

(2)、负整数：{ }；

(3)、非负数：{ }；

(4)、分数：{ }．

查看试题解析
21. 如图，已知四点 $A$ 、 $B$ 、 $C$ 、 $D$ ，请用尺规作图完成．（保留画图痕迹，不写作法）

(1)、画直线 $A B$ ；

(2)、画射线 $A C$

(3)、连接 $B C$ 并延长 $B C$ 到 $E$ ，使得 $C E = A B + A C$ ；

(4)、在线段 $B D$ 上取点 $P$ ，使 $P A + P C$ 的值最小．

(5)、在上述所画的图中，数一数，此时图中共有多少条线段？

查看试题解析
22. 计算：

(1)、 $- 3 \frac{1}{4} - (- \frac{1}{9}) + (- 6 \frac{3}{4}) + 1 \frac{8}{9}$

(2)、 $- 99 \frac{22}{23} \times 9$

(3)、 $- 1^{4} - (1 - 0 \times 4) \div \frac{1}{3} \times [{(- 2)}^{2} - 6]$

查看试题解析
23. 数学魔术：如图，数轴上的点A、B、C、D分别表示 $- 3$ 、 $- 1 \frac{1}{2}$ 、0、4，请回答下列问题．

(1)、在数轴上描出A、B、C、D四个点，用“ $<$ ”将4个数按照从小到大的顺序连接；

(2)、B、C两点间的距离是多少？A、D两点间的距离是多少？

(3)、点A、B、C、D的位置不动，现在把数轴的原点取在点B处，其余都不变，那么点A、B、C、D分别表示什么数？

查看试题解析
24. 如图，A、B、C三点在同一条直线上，点 $D$ 是线段 $A C$ 的中点，点 $E$ 是线段 $B C$ 的中点．

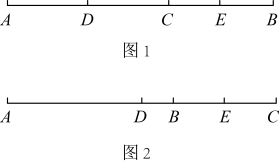(1)、如图1，点 $C$ 在线段 $A B$ 上，若 $A C = 6$ ， $B C = 4$ ，求线段 $D E$ 的长；

(2)、如图2，点 $C$ 在线段 $A B$ 的延长线上，若 $D E = 5$ ，求线段 $A B$ 的长．

查看试题解析
25. 在足球比赛中，根据场上攻守形势，守门员会在球门前来回跑动，如果以球门线为基准，向前跑记作正数，返回则记作负数，一段时间内，某守门员的跑动情况记录如下（单位： $m$ ）： $+ 10 ， - 2 ， + 5 ， - 6 ， + 12 ， - 9 ， + 4 ， - 14$ （假定开始计时时，守门员正好在球门线上）．

(1)、守门员最后是否回到了球门线上？

(2)、守门员在这段时间内共跑了多少米？

(3)、如果守门员离开球门线的距离超过 $10 m$ （不包括 $10 m$ ），那么对方球员挑射极有可能破门．请问在这段时间内，对方球员有几次挑射破门的机会？

查看试题解析
26. 已知O为直线 $A B$ 上一点，作射线 $O C 、 O D 、 O M$ ，且 $O M$ 平分 $∠ A O C$ ．

(1)、如图1，当 $O C 、 O D 、 O M$ 均在 $A B$ 上方时，若 $∠ C O D = 60 ° ， ∠ B O C = 10 °$ ，求 $∠ D O M$ 的度数；

(2)、如图2，当 $O C 、 O M$ 在 $A B$ 上方， $O D$ 在 $A B$ 的下方时，若 $∠ C O D = 9 0_{}^{0} ，$ $∠ A O D$ $： ∠ B O C = 1 ： 10$ ，求 $∠ D O M$ 的度数；

(3)、在（2）的条件下，作射线 $O P$ ，若 $∠ B O P$ 与 $∠ A O M$ 互余，请画出图形，并直接写出 $∠ C O P$ 的度数．

查看试题解析