河北省邯郸市永年区2023-2024学年九年级上学期期中数学试题

试卷更新日期：2023-12-20 类型：期中考试

进入出卷网下载

一、选择题（本大题共16个小题，1-10小题，每小题3分；11-16小题，每小题2分，共42分.在每小题给出的四个选项中，只有一项是符合题目要求的）

1. 甲、乙、丙、丁四名运动员进行百米测试，每人5次测试成绩的平均数都是13.4秒，方差分别为S_甲²＝0.73，S_乙²＝0.75，S_丙²＝0.69，S_丁²＝0.68，则这四名运动员百米成绩最稳定的是（）

A、甲 B、乙 C、丙 D、丁

查看试题解析
2. 为了弘扬我国古代数学发展的伟大成就，让学生深刻体会数学的魅力，某校举办了一次数学知识竞赛，并随机抽取了部分参赛学生的成绩，整理如表：
成绩/分
80
85
90
95
人数/人
4
6
8
2
根据表中的信息可知，这些参赛学生成绩的中位数和众数分别是（）

A、87.5，90 B、90，90 C、87.5，85 D、90，85

查看试题解析
3. 为了了解2023年某市九年级学生学业水平考试的数学成绩，从中随机抽取了1000名学生的数学成绩．下列说法正确的是（）

A、2023年该市九年级学生是总体 B、每一名九年级学生是个体 C、1000名九年级学生是总体的一个样本 D、样本容量是1000

查看试题解析
4. 用配方法解一元二次方程x²﹣4x＝5的过程中，配方正确的是（）

A、（x﹣2）²＝1 B、（x+2）²＝1 C、（x-2）²＝9 D、（x+2）²＝9

查看试题解析
5. 若x₁ ， x₂是一元二次方程x²﹣3x﹣10＝0的两个根，则x₁+x₂的值为（）

A、10 B、3 C、﹣10 D、﹣3

查看试题解析
6. 一元二次方程x²﹣x +1＝0的根的情况是（）

A、有两个相等的实数根 B、有两个不相等的实数根 C、只有一个实数根 D、没有实数根

查看试题解析
7. 如图，已知AB∥CD∥EF ， AD：DF＝2：3，若CE＝6，则BC的长为（）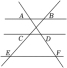

A、3 B、4 C、5 D、6

查看试题解析
8. 已知△ABC与△A'B'C'是位似图形，位似比是1：3，则△ABC与△A'B'C'的面积比是（）

A、1：3 B、1：6 C、1：9 D、3：1

查看试题解析
9. 如图，一辆自行车竖直摆放在水平地面上，右边是它的部分示意图，现测得∠A＝88°，∠C＝42°，AB＝60，则点A到BC的距离为（）

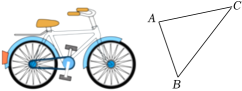A、60sin50° B、 $\frac{60}{s i n 5 0^{0}}$ C、60cos50° D、60tan50°

查看试题解析
10. 如图，商用手扶梯 $A B$ 的坡比为 $1 ： \sqrt{3}$ ，已知扶梯的长 $A B$ 为12米，则小明乘坐扶梯从 $B$ 处到 $A$ 处上升的高度 $A C$ 为（）

A、6米 B、 $6 \sqrt{3}$ 米 C、12米 D、 $12 \sqrt{3}$ 米

查看试题解析
11. 一鞋店试销一种新款女鞋，试销期间卖出情况如下表：
型号
22
22.5
23
23.5
24
24.5
25
数量/双
3
5
10
15
8
3
2
鞋店经理最关心哪种型号的鞋最畅销，则下列统计量最有意义的是（）

A、平均数 B、中位数 C、众数 D、方差

查看试题解析
12. 用12m长的铁丝围成一个一边靠墙的长方形场地，使该场地的面积为20m² ，并且在垂直于墙的一边开一个1m长的小门（用其它材料），若设垂直于墙的一边长为xm ，那么可列方程为（）

A、x（12﹣2x+1）＝20 B、 $x \cdot \frac{12 - 2 x + 1}{2} = 20$ C、 $x \cdot \frac{12 - 2 x - 1}{2} = 20$ D、x（12﹣2x﹣1）＝20

查看试题解析
13. 如图，在正方形ABCD中，E是BC的中点，F是CD上一点，AE⊥EF ， CF＝2，则AF的长为（）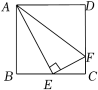

A、6 B、8 C、10 D、12

查看试题解析
14. 如图，一艘船由 $A$ 港沿北偏东65°方向航行 $30 \sqrt{2} km$ 至 $B$ 港，然后再沿北偏西40°方向航行至 $C$ 港， $C$ 港在 $A$ 港北偏东20°方向，则 $A$ ， $C$ 两港之间的距离为（） $km$ .

A、 $30 + 30 \sqrt{3}$ B、 $30 + 10 \sqrt{3}$ C、 $10 + 30 \sqrt{3}$ D、 $30 \sqrt{3}$

查看试题解析
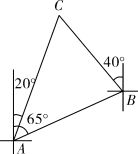15. 对于一元二次方程ax²+bx+c＝0（a≠0），下列说法：
①若a+b+c＝0，则b²﹣4ac≥0；
②若方程ax²+c＝0有两个不相等的实根，则方程ax²+bx+c＝0必有两个不相等的实根；
③若c是方程ax²+bx+c＝0的一个根，则一定有ac+b+1＝0成立；
④若x₀是一元二次方程ax²+bx+c＝0的根，则 $b^{2} - 4 a c = (2 a x {}_{0}+ b)^{2}$
⑤存在实数m、n（m≠n），使得am²+bm+c＝an²+bn+c；
其中正确的是（）

A、①②③④⑤ B、①②④⑤ C、①②④ D、①②③

查看试题解析
16. 如图，已知在矩形ABCD中，M是AD边的中点，BM与AC垂直，交直线AC于点N，连接DN，则下列四个结论中：①CN＝2AN；②DN＝DC；③tan∠CAD＝ $\sqrt{2}$ ；④△AMN∽△CAB.正确的有（）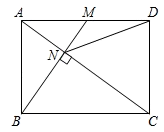

A、①②③④ B、①②③ C、①②④ D、②③④

查看试题解析

二、填空题(本大题共4个小题，每小题3分，共12分.把答案写在题中横线上)

17. 某公司要招聘一名职员，根据实际需要，从学历、经验和工作态度三个方面对甲、乙两名应聘者进行了测试．测试成绩如下表所示．如果将学历、经验和工作态度三项得分按2：1：3的比例确定两人的最终得分，并以此为依据确定录用者，那么将被录用（填甲或乙）

应聘者

项目

甲

乙

学历

9

8

经验

7

6

工作态度

5

7

查看试题解析
18. 据《墨经》记载，在两千多年前，我国学者墨子和他的学生做了“小孔成像”实验，阐释了光的直线传播原理．小孔成像的示意图如图所示，光线经过小孔O ，物体AB在幕布上形成倒立的实像CD（点A、B的对应点分别是C、D）．若物体AB的高为6cm ，小孔O到物体和实像的水平距离BE、CE分别为8cm、6cm ，则实像CD的高度为 cm ．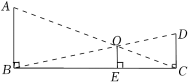

查看试题解析
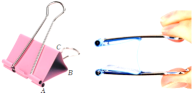
19. 如图，长尾夹的侧面是△ABC ，当AC与AB张开到互相平行时，达到最大夹纸厚度，已知AB＝AC＝15mm ， ∠ACB＝70°，则这个长尾夹最大夹纸厚度为 mm ．
（结果精确到1mm）
【参考数据：sin70°＝0.94，cos70°＝0.34，tan70°＝2.75】

查看试题解析
20. 如果关于x的一元二次方程ax²+bx+c＝0有两个实数根，且其中一个根为另外一个根的2倍，则称这样的方程为“倍根方程”，以下关于倍根方程的说法，正确的有（填序号）
①方程x²﹣x﹣2＝0是倍根方程；

②若（x﹣2）（mx+n）＝0是倍根方程：则4m²+5mn+n²＝0；

③若p，q满足pq＝2，则关于x的方程px²+3x+q＝0是倍根方程；

④若方程以ax²+bx+c＝0是倍根方程，则必有2b²＝9ac.

查看试题解析

三、解答题(本大题有6个小题，其中21题8分；22题10分，23题12分，24题10分；25题12分,26题14分；共66分.解答应写出文字说明、证明过程或演算步骤)

21. 解方程：

(1)、 ${(2 x + 3)}^{2} - 81 = 0$

(2)、 $y^{2} - 7 y + 6 = 0$

查看试题解析
22. 某校组织八、九年级各100名学生举行“喜迎二十大，奋进新征程”征文竞赛，现分别在八、九年级中各随机抽取10名学生的竞赛成绩（单位：分）进行统计、整理如下：
收集数据：
八年级：74，76，79，81，84，86，87，90，90，93．
九年级：76，81，81，83，84，84，84，85，90，92．
整理数据：
八、九年级竞赛成绩各分数段整理如下：

70≤x＜80
80≤x＜90
90≤x＜100
八年级
a
4
3
九年级
1
7
2
分析数据：
八、九年级成绩的平均数、中位数、众数和方差整理如下：

平均数
中位数
众数
方差
八年级
84
b
90
36.4
九年级
84
84
c
18.4
问题解决：
根据以上信息，解答下列问题：

(1)、直接写出a＝， b＝， c＝．

(2)、根据上述数据分析，该校八、九年级中哪个年级的竞赛成绩更优异？请说明理由（写出一条理由即可）．

(3)、规定竞赛成绩不低于85分记为“优秀”，请分别估计这两个年级竞赛成绩达到“优秀”的学生人数．

查看试题解析
23. 一款服装每件进价为80元，销售价为120元时，每天可售出20件，为了扩大销售量，增加利润，经市场调查发现，如果每件服装降价1元，那么平均每天可多售出2件．

(1)、设每件衣服降价x元，则每天销售量增加件，每件商品盈利
元（用含x的代数式表示）；

(2)、每件服装降价多少元时，商家平均每天能盈利1200元；

(3)、商家能达到平均每天盈利1800元吗？请说明你的理由．

查看试题解析
24.
如图，在△ABC中，AD⊥BC，BE⊥AC，垂足分别为D，E，AD与BE相交于点F．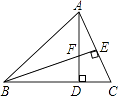

(1)、求证：△ACD∽△BFD；

(2)、当tan∠ABD=1，AC=3时，求BF的长．

查看试题解析
25. 图1是某小区入口实景图，图2是该入口抽象成的平面示意图．已知入口BC宽3.9米，门卫室外墙AB上的O点处装有一盏路灯，点O与地面BC的距离为3.3米，灯臂OM长为1.2米（灯罩长度忽略不计），∠AOM＝60°．

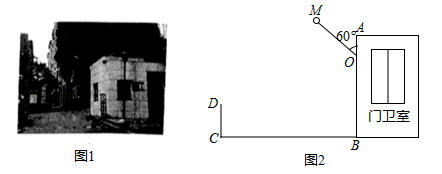(1)、求点M到地面的距离；

(2)、某搬家公司一辆总宽2.55米，总高3.5米的货车从该入口进入时，货车需与护栏CD保持0.65米的安全距离，此时，货车能否安全通过？若能，请通过计算说明；若不能，请说明理由．（参考数据： $\sqrt{3} \approx$ 1.73，结果精确到0.01米）

查看试题解析
26. 如图，在矩形 $A B C D$ 中， $A B = 16 cm$ ， $B C = 6 cm$ ，动点P、Q分别以 $3 cm/s$ ， $2 cm/s$ 的速度从点A ， C同时出发，沿规定路线移动．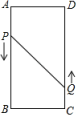

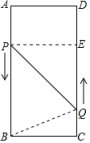(1)、若点P从点A移动到点B停止，点Q随点P的停止而停止移动，问经过多长时间P ， Q两点之间的距离是 $10 cm$ ？

(2)、若点P沿着 $A B \to B C \to C D$ 移动，点Q从点C移动到点D停止时，点P随点Q的停止而停止移动，试探求经过多长时间 $△ P B Q$ 的面积为 $12 {cm}^{2}$ ？

查看试题解析

	平均数	中位数	众数	方差
八年级	84	b	90	36.4
九年级	84	84	c	18.4

成绩/分	80	85	90	95
人数/人	4	6	8	2

型号	22	22.5	23	23.5	24	24.5	25
数量/双	3	5	10	15	8	3	2

应聘者项目	甲	乙
学历	9	8
经验	7	6
工作态度	5	7

	70≤x＜80	80≤x＜90	90≤x＜100
八年级	a	4	3
九年级	1	7	2