河北省张家口市张北县2023-2024学年九年级上学期期中数学试题
试卷更新日期:2023-12-20 类型:期中考试
一、选择题(本次题共15个小题,共38分.1~6小题各3分.7~16小题各2分在每小题给出的四个选项中,只有一项是符合题目要求的)
-
1. 点关于原点对称的点的坐标是( )A、 B、 C、 D、2. 下列抛物线经过原点的是( )A、 B、 C、 D、3. 下列方程最适合用配方法求解的是( )A、 B、 C、 D、4. 已知的直径为10,直线l与相交,则圆心O到直线l的距离可能是( )A、4 B、5 C、6 D、85. 一个不遇明的盒子中装有10个除颜色外无其他差别的小球,其中有1个黄球和3个绿球,其余都是红球,从中随机摆出一个小球.下列判断正确的是( )
甲:摸到红球比摸到黄球的可能性大;乙:摸到红球的概率为
A、甲、乙都对 B、甲、乙都不对 C、只有甲对 D、只有乙对6. 在新型俄罗斯方块游戏中(出现的图案可进行顺时针、逆时针旋转.向左、向右平移)。已拼好的图形如图所示.现又出现一个图案正向下运动,若要使该图案与下面的图形拼成一个完整的矩形。则该图案需进行的操作是( ) A、顺时针旋转90°,向右平移至最右侧 B、逆时针旋转90°,向右平移至最右侧 C、顺时针旋转90°,向左平移至最左侧 D、逆时针旋转90°,向左平移至最左侧7. 在坐标系中,若想使抛物线平移后经过原点O , 则平移的方式可能是( )A、向上平移2个单位长度 B、向下平移2个单位长度 C、向左平移2个单位长度 D、向右平移2个单位长度8. 如图,在正方形网格中,A , B , C , D , E , F , G , H , M , N是网格线交点。与关于某点对称。则其对称中心是( )
A、顺时针旋转90°,向右平移至最右侧 B、逆时针旋转90°,向右平移至最右侧 C、顺时针旋转90°,向左平移至最左侧 D、逆时针旋转90°,向左平移至最左侧7. 在坐标系中,若想使抛物线平移后经过原点O , 则平移的方式可能是( )A、向上平移2个单位长度 B、向下平移2个单位长度 C、向左平移2个单位长度 D、向右平移2个单位长度8. 如图,在正方形网格中,A , B , C , D , E , F , G , H , M , N是网格线交点。与关于某点对称。则其对称中心是( )
 A、点G B、点H C、点M D、点N9. 某种油菜籽在相同条件下发芽试验的结果如下表所示,一般地,在相同条件下,2000粒油菜籽中不能发芽的约有( )
A、点G B、点H C、点M D、点N9. 某种油菜籽在相同条件下发芽试验的结果如下表所示,一般地,在相同条件下,2000粒油菜籽中不能发芽的约有( )油菜籽粒数n
100
200
400
600
800
1000
发芽的粒数m
95
193
382
582
768
961
发芽的频率
0.95
0.965
0.955
0.97
0.96
0.961
A、1920粒 B、960粒 C、80粒 D、40粒10. 如图,一条公路环绕山脚的部分是一段圆弧形状(O为圆心),过A、B两点的切线交于点C , 测得 , A , B两点之间的距离为72米。则这段公路AB的长度为( ) A、12π米 B、24π米 C、36π米 D、48π米11. 漠淇初一时的体重是40kg,到初三时,体重增加到48.4kg,则他的体重早均每年的增长率为( )A、5% B、10% C、15% D、20%12. 如图,点是的六等分点.若 , 的周长分别为 , , 面积分别为 , , 则下列正确的是( )
A、12π米 B、24π米 C、36π米 D、48π米11. 漠淇初一时的体重是40kg,到初三时,体重增加到48.4kg,则他的体重早均每年的增长率为( )A、5% B、10% C、15% D、20%12. 如图,点是的六等分点.若 , 的周长分别为 , , 面积分别为 , , 则下列正确的是( )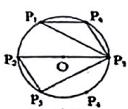 A、 B、 C、 D、13. 关于x的方程的根的情况是( )A、无实数根 B、有两个不相等的实数根 C、有两个实数根 D、无法确定14. 关于x的二次函数和一次函数(a、c都是常数,且)在同一平面直角坐标系中的图象可能是( )A、
A、 B、 C、 D、13. 关于x的方程的根的情况是( )A、无实数根 B、有两个不相等的实数根 C、有两个实数根 D、无法确定14. 关于x的二次函数和一次函数(a、c都是常数,且)在同一平面直角坐标系中的图象可能是( )A、 B、
B、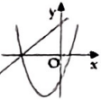 C、
C、 D、
D、 15. 某题市以每件10元的价格购进一种文具.经过市场调查发现,该文具每天的销售数量y(件)与销售单价x(元)()之间满足 , 则销售这种文具每天可得( )A、最大利润150元 B、最大利润128元 C、最小利润150元 D、最小利润120216. 如图,在中, , , . O是边AB上一点,以点O为圆心,OA长为半径在边AB的右侧作半圆O , 交边AB于点P , 交边AC于点Q . 关于结论Ⅰ,Ⅱ,下列判断正确的是( )
15. 某题市以每件10元的价格购进一种文具.经过市场调查发现,该文具每天的销售数量y(件)与销售单价x(元)()之间满足 , 则销售这种文具每天可得( )A、最大利润150元 B、最大利润128元 C、最小利润150元 D、最小利润120216. 如图,在中, , , . O是边AB上一点,以点O为圆心,OA长为半径在边AB的右侧作半圆O , 交边AB于点P , 交边AC于点Q . 关于结论Ⅰ,Ⅱ,下列判断正确的是( )
结论Ⅰ:当BQ的长度最短时,半圆O的单径为
结论Ⅱ:当时,BQ与半圆O相切,且
A、只有结论Ⅰ B、只有结论Ⅱ对 C、结论Ⅰ、Ⅱ都对 D、结论Ⅰ、Ⅱ都不对二、填空题(本大题共3个小题,共10分.17分题2分,18~19小题各4分。每空2分)
-
17. 杜牧《清明》诗中写道“清明时节雨纷纷”,从数学的观点看,诗句中描述的事件是(填“必然”或“随机”)事件.18. 如图,的半径于点D,连接AO并延长 , 交于点B , 连接BE.

⑴若 , 则的度数为。
⑵若 , , 则的半径长为。
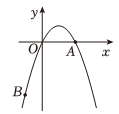
19. 如图,抛物线与x轴的正半轴交于点A , 点在该抛物线上.⑴m的值为;
⑵连接AB , P是直线AB上的动点,将点P向左平移5个单位长度得到点Q . 若线段PQ与抛物线只有一个公共点,则点P的横坐标x的取值范围为。
三、解答题(本次题共7个小题,共72分.解答应写出文字说明。证明过程或演算步骤)
-
20. 如图,在平面直角坐标系中,的三个顶点的坐标分别是 , , , 将绕点逆时针旋转得到(点的对应点为点),且点在边上.
 (1)、旋转角的度数为;的长为;的长为 .(2)、将绕点顺时针旋转90°得到 , 请在图中画出 , 并直接写出点的坐标.21. 如图1,约定:上方相邻两数之和等于这两数下方箭头共同指向的数.示例如图2,即 .
(1)、旋转角的度数为;的长为;的长为 .(2)、将绕点顺时针旋转90°得到 , 请在图中画出 , 并直接写出点的坐标.21. 如图1,约定:上方相邻两数之和等于这两数下方箭头共同指向的数.示例如图2,即 .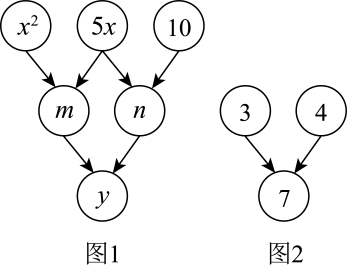 (1)、当时,求的值;(2)、当时,求的值.22. 第19届亚运会于2023年9月23日至10月8日在杭州举行,此次赛会共召集3.76万名志愿者.在对项目A.排球;B.羽毛球;C.藤球分配志愿者时(每名志愿者被随机分配到一个项目中进行志愿服务)。嘉嘉和淇淇也在其中。
(1)、当时,求的值;(2)、当时,求的值.22. 第19届亚运会于2023年9月23日至10月8日在杭州举行,此次赛会共召集3.76万名志愿者.在对项目A.排球;B.羽毛球;C.藤球分配志愿者时(每名志愿者被随机分配到一个项目中进行志愿服务)。嘉嘉和淇淇也在其中。 (1)、求嘉嘉被分到排球项目的概率;(2)、请补全如图所示的树状图,并分析嘉嘉和淇淇被分到相同项目的概率和不同项目的概率哪个较大.23. 如图1.正方形ABCD内接于 , 连接AC . P是上的动点(不与点A重合),连接AP .
(1)、求嘉嘉被分到排球项目的概率;(2)、请补全如图所示的树状图,并分析嘉嘉和淇淇被分到相同项目的概率和不同项目的概率哪个较大.23. 如图1.正方形ABCD内接于 , 连接AC . P是上的动点(不与点A重合),连接AP . (1)、如图2,当P是的中点时,过点D作的切线,与AP的延长线交于点Q .
(1)、如图2,当P是的中点时,过点D作的切线,与AP的延长线交于点Q .①AC与DQ之间的位置关系是 ▲ 。并说明理由;
②求的度数;
(2)、连接DP , 请直接写出的度数。24. 如图.取某一位置的水平线为x轴.建立平面直角坐标系后,小山坡AB可近似地看成抛物线:的一部分.小球在离点A3m的点C处抛出.落在山坡的点D处(点D在小山坡AB的坡顶的右侧),小球的运动轨迹为抛物线:的一部分. (1)、求小山坡AB的坡顶高度;(2)、若测得点D的高度为3m,求抛物线的函数解析式(不要求写自变量x的取值范围);(3)、当小球运动到坡顶正上方,且与坡顶距离超过3米时,请直接写出b的取值范围.25. 在矩形中, , , 连接AC , . 将半圆形量角器放在如图1所示的位置,其直径在边上,点E是量角器上的零刻度,交AC于点F , 点O是半圆形量角器所在圆的圆心.
(1)、求小山坡AB的坡顶高度;(2)、若测得点D的高度为3m,求抛物线的函数解析式(不要求写自变量x的取值范围);(3)、当小球运动到坡顶正上方,且与坡顶距离超过3米时,请直接写出b的取值范围.25. 在矩形中, , , 连接AC , . 将半圆形量角器放在如图1所示的位置,其直径在边上,点E是量角器上的零刻度,交AC于点F , 点O是半圆形量角器所在圆的圆心. (1)、求点F在半圆形量角器上的读数;(2)、将半圆形量角器绕点A顺时针旋转 . 将半圆形量角器绕点A顺时针旋转α(0°≤α≤180°).
(1)、求点F在半圆形量角器上的读数;(2)、将半圆形量角器绕点A顺时针旋转 . 将半圆形量角器绕点A顺时针旋转α(0°≤α≤180°).
①当点E旋转到AC上时,交AB于点M,如图2所示.求证:BC与半圆形量角器相切;
②在旋转过程中,当与直线BC只有一个交点(不包括端点A,E)时,设此交点与点C的距离为d,请直接写出d的取值范围.26. 如图,抛物线:与轴交于A , B两点(点A在点B的左侧),与轴交于点 , 且 , 为抛物线的对称轴右侧上的点(不含顶点)。 (1)、求的值和抛物线的顶点坐标;(2)、设抛物线在点和点之间部分(含点和点)的最高点与最低点的纵坐标之差为 , 求与的函数解析式,并写出自变量的取值范围;(3)、当点的坐标满足时,连接 . 将直线与抛物线围成的封闭图形记为 .
(1)、求的值和抛物线的顶点坐标;(2)、设抛物线在点和点之间部分(含点和点)的最高点与最低点的纵坐标之差为 , 求与的函数解析式,并写出自变量的取值范围;(3)、当点的坐标满足时,连接 . 将直线与抛物线围成的封闭图形记为 .①求点的坐标;
②直接写出封闭图形的边界上的整点(横、纵坐标都是整数的点)的个数.