河北省承德市兴隆县2023-2024学年八年级上学期期中数学试题
试卷更新日期:2023-12-20 类型:期中考试
一、选择题(本大题共16个小题,1-6每小题3分,7-16每小题2分,共38分.在每个小题给出的四个选项中,只有一项是符合题目要求的)
-
1. 下列分式中,是最简分式的是( )A、 B、 C、 D、2. 下列四个数 , , , 中,无理数是( )A、 B、 C、 D、3. 如图所示,AB∥CD,AB=CD,BE=DF,则图中的全等三角形有( )
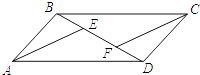 A、2对 B、3对 C、4对 D、5对4. 若表示的是一个最简分式,则☆可以是( )A、2x B、x C、 D、5. 若分式有意义,则x的取值范围是( )A、 B、 C、 D、6. 下列说法中,正确的是( )A、无理数包括正无理数、零和负无理数 B、无限小数都是无理数 C、实数可以分为正实数和负实数两类 D、正实数包括正有理数和正无理数7. 下列运算中正确的是( )A、 B、 C、 D、8. 如图,B,D分别是位于线段AC两侧的点,连接AB,AD,CB,CD,则下列条件中,与AB=AD相结合无法判定△ABC≌△ADC的是( )
A、2对 B、3对 C、4对 D、5对4. 若表示的是一个最简分式,则☆可以是( )A、2x B、x C、 D、5. 若分式有意义,则x的取值范围是( )A、 B、 C、 D、6. 下列说法中,正确的是( )A、无理数包括正无理数、零和负无理数 B、无限小数都是无理数 C、实数可以分为正实数和负实数两类 D、正实数包括正有理数和正无理数7. 下列运算中正确的是( )A、 B、 C、 D、8. 如图,B,D分别是位于线段AC两侧的点,连接AB,AD,CB,CD,则下列条件中,与AB=AD相结合无法判定△ABC≌△ADC的是( )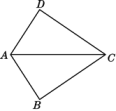 A、CB=CD B、∠BAC=∠DAC C、∠BCA=∠DCA D、以上都无法判定9. 一个正方体的水晶砖,体积为 , 它的棱长大约在( )A、3cm与4cm之间 B、4cm与5cm之间 C、5cm与6cm之间 D、6cm与7cm之间10. 已知 , 则的值为( )A、 B、 C、4 D、-411. 如图,已知 , 则甲、乙、丙三个三角形中和全等的是( )
A、CB=CD B、∠BAC=∠DAC C、∠BCA=∠DCA D、以上都无法判定9. 一个正方体的水晶砖,体积为 , 它的棱长大约在( )A、3cm与4cm之间 B、4cm与5cm之间 C、5cm与6cm之间 D、6cm与7cm之间10. 已知 , 则的值为( )A、 B、 C、4 D、-411. 如图,已知 , 则甲、乙、丙三个三角形中和全等的是( ) A、只有乙 B、甲和乙 C、只有丙 D、乙和丙12. 如图,数轴上点A表示的数可能是( )
A、只有乙 B、甲和乙 C、只有丙 D、乙和丙12. 如图,数轴上点A表示的数可能是( )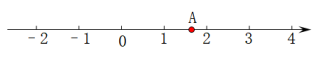 A、7的算术平方根 B、6的立方根 C、9的平方根 D、8的立方根13. 如图,已知中, , 点D在底边BC上,添加下列条件后,仍无法判定的是( )
A、7的算术平方根 B、6的立方根 C、9的平方根 D、8的立方根13. 如图,已知中, , 点D在底边BC上,添加下列条件后,仍无法判定的是( )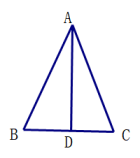 A、 B、 C、 D、 ,14. 如图,△ABC的顶点A、B、C都在小正方形的顶点上,在格点F、G、H、I中选出一个点与点D、点E构成的三角形与△ABC全等,则符合条件的点共有( )
A、 B、 C、 D、 ,14. 如图,△ABC的顶点A、B、C都在小正方形的顶点上,在格点F、G、H、I中选出一个点与点D、点E构成的三角形与△ABC全等,则符合条件的点共有( ) A、1个 B、2个 C、3个 D、4个15. 已知: , , , 则a , b , c大小关系是( )A、 B、 C、 D、16. 如图①,某品牌饮料的包装箱是一个长、宽、高分别为a , b , 4r的长方体纸箱,饮料瓶可近似看成底面半径为r , 高为4r的圆柱体.如图②,若纸箱里装满了一层饮料,那么纸箱的空间利用率(听装饮料总体积与纸箱体积的比)为( )
A、1个 B、2个 C、3个 D、4个15. 已知: , , , 则a , b , c大小关系是( )A、 B、 C、 D、16. 如图①,某品牌饮料的包装箱是一个长、宽、高分别为a , b , 4r的长方体纸箱,饮料瓶可近似看成底面半径为r , 高为4r的圆柱体.如图②,若纸箱里装满了一层饮料,那么纸箱的空间利用率(听装饮料总体积与纸箱体积的比)为( )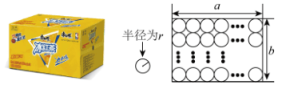 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(本大题共3个小题,5个空,每空2分,共10分.)
-
17. 已知a+ =3,则a2+ 的值是 .18. 如图,在与中,E在BC边上, , , , 若 , 则 , .
 19. 如图,面积为3的正方形的顶点A在数轴上,对应的数为1,以点A为圆心,长为半径画弧交数轴于点E(点E位于点A的左侧),则线段 , 点E对应的数为 .
19. 如图,面积为3的正方形的顶点A在数轴上,对应的数为1,以点A为圆心,长为半径画弧交数轴于点E(点E位于点A的左侧),则线段 , 点E对应的数为 .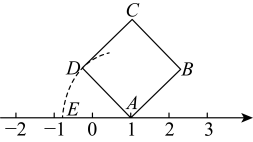
三、解答题(本大题共7个小题,共72分.解答应写出文字说明、证明过程或演算步骤)
-
20.(1)、先化简,再求值: , 其中.(2)、解方程:.21. 如图,在和中,点A , E , F , C在同一直线上,有下面四个论断:
⑴;⑵;⑶;⑷.请将其中三个论断作为条件,余下的一个作为结论,编一证明题,并写出证明过程.
 22. “孔子周游列国”是流传很广的故事.有一次他和弟子颜回等到离所住驿站30里的书院讲学,弟子们步行出发1小时后,孔子坐牛车出发,已知牛车的速度是步行的1.5倍,结果孔子和弟子们同时到达书院,求孔子及其弟子们的速度各是多少里/小时.23. 某小区准备修建一个面积为的花坛,甲、乙两个工程队给出如下两个施工方案.
22. “孔子周游列国”是流传很广的故事.有一次他和弟子颜回等到离所住驿站30里的书院讲学,弟子们步行出发1小时后,孔子坐牛车出发,已知牛车的速度是步行的1.5倍,结果孔子和弟子们同时到达书院,求孔子及其弟子们的速度各是多少里/小时.23. 某小区准备修建一个面积为的花坛,甲、乙两个工程队给出如下两个施工方案.甲:花坛为长方形,且长与宽的比为.
乙:花坛为正方形.
 (1)、求长方形花坛的宽.(2)、嘉淇说:“正方形花坛的边长肯定比长方形花坛的宽长3m.”请你判断嘉淇的说法是否正确,并通过计算说明.24. 如图,已知.
(1)、求长方形花坛的宽.(2)、嘉淇说:“正方形花坛的边长肯定比长方形花坛的宽长3m.”请你判断嘉淇的说法是否正确,并通过计算说明.24. 如图,已知. (1)、作 , 使与在AC的异侧,并且(要求:尺规作图、保留作图痕迹,不写作法);(2)、连接BD , 交AC于O , 试说明.25. 数学来源于生活,生活离不开数学,开水中加入适量的糖冲泡成甜糖水很受一些人的喜爱,人们常用糖水中糖与糖水的比表示糖水的甜度.(1)、若在a克糖水里面含糖b克(),则该糖水的甜度为;(2)、现向(1)中的糖水中再加入适量的糖,充分搅匀后,感觉糖水更甜了.
(1)、作 , 使与在AC的异侧,并且(要求:尺规作图、保留作图痕迹,不写作法);(2)、连接BD , 交AC于O , 试说明.25. 数学来源于生活,生活离不开数学,开水中加入适量的糖冲泡成甜糖水很受一些人的喜爱,人们常用糖水中糖与糖水的比表示糖水的甜度.(1)、若在a克糖水里面含糖b克(),则该糖水的甜度为;(2)、现向(1)中的糖水中再加入适量的糖,充分搅匀后,感觉糖水更甜了.请用所学的数学知识解释这一现象.(提示:我们在判断两个数的大小时,常常会用到作差法,如所以 , 同样如果 , 就说明)
26. 如图,等腰和等腰中腰为AB、AC、AD , 底角 , 将一块三角板中用含角的顶点与A点重合,并将三角板绕A点按逆时针方向旋转.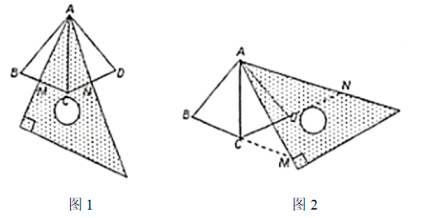 (1)、当三角板旋转到如图1的位置时,三角板的两边与等腰三角形的两底边分别相交于M、N两点,求证:;(2)、当三角板旋转到如图2的位置时,三角板的两边与等腰三角形两底边的延长线分别相交于M、N两点,(1)的结论还成立吗?请说明理由.
(1)、当三角板旋转到如图1的位置时,三角板的两边与等腰三角形的两底边分别相交于M、N两点,求证:;(2)、当三角板旋转到如图2的位置时,三角板的两边与等腰三角形两底边的延长线分别相交于M、N两点,(1)的结论还成立吗?请说明理由.