河北省廊坊市大城县2023-2024学年九年级上学期期中数学试题

试卷更新日期：2023-12-20 类型：期中考试

进入出卷网下载

一、选择题（本大题共16个小题，共38分．1~6小题各3分，7~16小题各2分，在每小题给出的四个选项中，只有一项是符合题目要求的）

1. 下列选项中的图形属于中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 抛物线 $y = x^{2} - 1$ 的顶点坐标是（）

A、 $(0 ， 1)$ B、 $(0 ， - 1)$ C、 $(1 ， 0)$ D、 $(- 1 ， 0)$

查看试题解析
3. 一个不透明的袋子中装有4个黑球，1个白球，每个球除颜色外都相同，从中任意摸出1个球，对于甲、乙的说法，下列判断正确的是（）
甲：若摸出的球是白球，则该事件属于随机事件；乙：摸到黑球比摸到白球的可能性大

A、只有甲对 B、只有乙对 C、甲、乙都对 D、甲、乙都不对

查看试题解析
4. 用配方法解方程 $x^{2} - 2 x - 5 = 0$ 时，原方程应变形为（）

A、 ${(x + 1)}^{2} = 6$ B、 ${(x + 2)}^{2} = 9$ C、 ${(x - 1)}^{2} = 6$ D、 ${(x - 2)}^{2} = 9$

查看试题解析
5. 如图，转盘中6个扇形的面积都相等．任意转动转盘1次，当转盘停止转动时，事件“指针指向扇形中的数大于4”的概率为（）

A、 $\frac{5}{6}$ B、 $\frac{1}{2}$ C、 $\frac{1}{3}$ D、 $\frac{1}{6}$

查看试题解析
6. 在平面直角坐标系 $x O y$ 中，以点 $A (1 ， 3)$ 为圆心， $2$ 为半径作 $⊙ A$ ，下列判断正确的是（）

A、 $⊙ A$ 与 $x$ 轴相交 B、 $⊙ A$ 与 $y$ 轴相切 C、点 $O$ 在 $⊙ A$ 外 D、点 $(1 ， 1)$ 在 $⊙ A$ 内

查看试题解析
7. 在做抛硬币试验时，抛掷n次，若正面向上的次数为m次，则记正面向上的频率 $P = \frac{m}{n}$ ．下列说法正确的是（　　）

A、P一定等于 $\frac{1}{2}$ B、P一定不等于 $\frac{1}{2}$ C、多抛一次，P更接近 $\frac{1}{2}$ D、随着抛掷次数的逐渐增加，P稳定在 $\frac{1}{2}$ 附近

查看试题解析
8. 如图， $A B$ 为 $⊙ O$ 的切线，B为切点， $A O$ 交 $⊙ O$ 于点C ，点D在优弧 $\overset{⌢}{B D C}$ 上，若 $∠ D = 24 °$ ，则 $∠ A$ 的度数为（）

A、 $48 °$ B、 $42 °$ C、 $58 °$ D、 $52 °$

查看试题解析
9. 如图，正五边形 $A B C D E$ 内接于半径为3的 $⊙ O$ ，则阴影部分的面积为（）

A、 $\frac{18 π}{5}$ B、 $\frac{12 π}{5}$ C、 $\frac{9 π}{5}$ D、 $\frac{6 π}{5}$

查看试题解析
10. 如图，坐标平面上有一个透明胶片，透明胶片上有一条抛物线及抛物线上一点P ，且抛物线为 $y = x^{2}$ ，点P的坐标是 $(2 ， 4)$ ．若将此透明胶片进行平移后，使点P的坐标为 $(0 ， 3)$ ，则此时抛物线的解析式为（）

A、 $y = {(x + 2)}^{2} + 1$ B、 $y = {(x + 2)}^{2} - 1$ C、 $y = {(x - 2)}^{2} + 1$ D、 $y = {(x - 2)}^{2} - 1$

查看试题解析
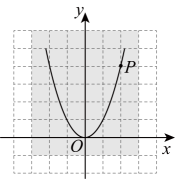11. 小明准备完成题目：解一元二次方程 $x^{2} - 4 x + □ = 0$ ．若“□”表示一个数字，且方程 $x^{2} - 4 x + □ = 0$ 有实数根，则“□”的值可能为（）

A、4 B、5 C、6 D、7

查看试题解析
12. 如图，在 $△ A B C$ 中， $∠ A C B = 90 ° ， ∠ A = 35 °$ ．将 $△ A B C$ 绕点C顺时针旋转到 $△ A^{'} B^{'} C$ ，旋转角为 $α (0 ° < α < 180 °)$ ．当点B的对应点 $B^{'}$ 恰好落在边 $A B$ 上时，旋转角 $α$ 的度数为（）

A、 $35 °$ B、 $55 °$ C、 $65 °$ D、 $70 °$

查看试题解析
13. 函数 $y = a x^{2} - 2 x + 1 (a \neq 0)$ 在平面直角坐标系中的图象可能是（）

A、 B、 C、 D、

查看试题解析
14. 商场将进价为50元/件的某种商品以80元/件出售时每天能卖出30件．经调查发现，每降价1元，每天可多卖出5件，若降价 $x$ 元，每天将盈利1080元，则可列方程为（）

A、 $(80 - x) (30 + x) = 1080$ B、 $(80 - x) (30 + 5 x) = 1080$ C、 $(80 - 50 - x) (30 + x) = 1080$ D、 $(80 - 50 - x) (30 + 5 x) = 1080$

查看试题解析
15. 如图，抛物线 $y = (1 - x) (x + 3)$ 与x轴负半轴，y轴分别交于点A ， B ，现要在 $A B$ 段的抛物线上找点 $P (m ， n)$ ，关于针对n的不同取值，所找点P的个数，甲、乙两人的说法如下，下列判断正确的是（）
甲：若 $n = 4$ ，则点P的个数为2；乙：若 $0 < n < 3$ ，则点P的个数为1

A、只有甲对 B、只有乙对 C、甲、乙都对 D、甲、乙都不对

查看试题解析
16. 题目：“如图，在等腰直角三角形 $A B C$ 中， $∠ A B C = 90 °$ ，以点 $A$ 为圆心，以小于 $A B$ 的长度为半径作 $⊙ A$ ， $P$ 是 $⊙ A$ 上一点，连接 $B P$ ．将线役 $B P$ 绕点 $B$ 顺时针旋转 $90 °$ 得到线段 $B P^{'}$ ，连接 $P P^{'}$ ．当 $∠ A P B$ 为何度数时， $P P^{'}$ 与 $⊙ A$ 相切，切点为 $P$ ？”对于其答案，甲答： $∠ A P B = 135 °$ ，乙答： $∠ A P B = 60 °$ ，丙答： $∠ A P B = 45 °$ ，则下列判断正确的是（）

A、只有甲答的对 B、甲、丙答案合在一起才完整 C、乙、丙答案合在一起才完整 D、三人答案合在一起才完整

查看试题解析

二、填空题（本大题共3个小题，共10分．17小题2分，18~19小题各4分，每空2分）

17. 在平面直角坐标系中，点 $(1 ， - 1)$ 关于原点对称的点的坐标为．

查看试题解析
18. 如图，点D是 $△ A B C$ 的内心， $A D$ 的延长线和 $△ A B C$ 的外接圆相交于点E ，连接 $B E$ ， $C E$ ，且 $∠ B A C = 50 °$ ；
$∠ B E C$ 的度数为；
$∠ B C E$ 的度数为．

查看试题解析
19. 如图，已知平面直角坐标系中的四个点： $A (0 ， 2)$ ， $B (1 ， 0)$ ， $C (3 ， 1)$ ， $D (2 ， 3)$ ．

若抛物线 $y = \frac{2}{3} x^{2} + b x + c$ 经过点A ， B ，则当 $x \geq$ 时，y随x的增大而增大；
若抛物线 $y = a x^{2} + b x + c$ 经过A ， B ， C ， D四点中的三个点，则满足条件的a的最大值为．

查看试题解析

三、解答题（本大题共7个小题，共72分，解答应写出文字说明、证明过程或演算步骤）

20. 用适当的方法解下列方程．

(1)、 $x^{2} + x - 6 = 0$ ；

(2)、 ${(x + 3)}^{2} = 2 (x + 3)$ ．

查看试题解析
21. 如图，在平面直角坐标系中， $△ A B C$ 的三个顶点分别是 $A (1 ， 3)$ ， $B (4 ， 4)$ ， $C (2 ， 1)$ ．

(1)、在图中画出 $△ A_{1} B_{1} C_{1}$ ，使得 $△ A_{1} B_{1} C_{1}$ 与 $△ A B C$ 关于点 $O$ 对称；

(2)、在（1）的基础上，画出 $△ A_{1} B_{1} C_{1}$ 绕点 $O$ 逆时针旋转 $90 °$ 后的 $△ A_{2} B_{2} C_{2}$ ，并直接写出点 $B_{2}$ 的坐标．

查看试题解析
22. 嘉嘉和淇淇周末相约到公园展练，公园有A ， B两个入口，他们可以随机选择一个入口进入，假设选择每个入口的可能性相同．

(1)、嘉嘉选择从A入口进入公园的概率为；

(2)、补全如图所示的树状图，并求两人选择不同入口进入公园的概率．

查看试题解析
23. 图1是某型号汤碗，截面如图2所示，碗体部分为半圆O ，直径 $A B = 20 c m$ ，倒汤时， $∠ C A B = 60 °$ ，如图3所示．

(1)、 $∠ C O B$ 的度数为；

(2)、在图3中，通过计算比较直径 $A B$ 与 $\overset{⌢}{C B}$ 的长度哪个更长；

(3)、请在图3中画出线段 $M N$ ，用其长度表示汤（阴影部分）的最大深度（不说理由），并求汤的最大深度．

查看试题解析
24. 已知抛物线 $y = x^{2} + a x + a + 1$ 经过点 $A (- 2 ， 3)$ ．

(1)、求a的值；

(2)、已知点 $P (m ， y_{P}) ， Q (m - 4 ， y_{Q})$ 均在该抛物线上．
①若 $m = 0$ ，请直接比较 $y_{P}$ 与 $y_{Q}$ 的大小关系；
②当 $- 3 \leq x \leq m$ 时，函数 $y$ 的最大值是 $6$ ，最小值是 $2$ ，求 $m$ 的取值范围．

查看试题解析
25. 如图， $⊙ O$ 的半径为1，C是 $⊙ O$ 直径 $A B$ 延长线上一点，点D在 $⊙ O$ 上， $∠ A = ∠ C D B$ ．

(1)、求证：直线 $C D$ 是 $⊙ O$ 的切线；

(2)、已知 $∠ C D B = ∠ C$ ，点P在 $A B$ 上方的 $⊙ O$ 上运动（不与点A ， B重合），连接 $A P ， D P$ ．
①求 $∠ A P D$ 的度数；
②过点D作 $D P$ 的垂线，交 $P A$ 的延长线于点Q ，求 $D Q$ 的最大长度．

查看试题解析
26. 过山车是倍受年轻人喜爱的经典娱乐项目．如图14， $A \to B \to C$ 为过山车的一部分轨道（B为轨道与地面的交点，图中的x轴表示地面），它可以看成抛物线 $y = a x^{2} + b x + c (a \neq 0)$ 的一部分，其中 $O B = 20$ 米（轨道厚度忽略不计）．

(1)、写出a ， b之间的数量关系；

(2)、已知 $O A = 50$ 米．
①求抛物线 $y = a x^{2} + b x + c (a \neq 0)$ 的解析式；
②在轨道距离地面32米处有两个位置M和C ，当过山车运动到点C处时，沿着平行于地面的轨道向前运动了18米至点G ，又进入下坡段 $G \to H$ （G接口处轨道忽略不计，点H为轨道与地面的交点）．已知轨道抛物线 $G \to H \to K$ 的形状与抛物线 $M \to B \to C$ 的形状相同，求 $O H$ 的长度；
③现需要在轨道下坡段 $A \to B$ 进行一种安全加固，建造某种材料的水平和竖直支架 $P E$ ， $P T ， Q F ， Q S$ ，且要求 $2 O T = O S$ ，如图所示，已知这种材料的价格是5000元/米．当PE的长度为多少时会使造价最低？并求最低造价为多少元？

查看试题解析