2023-2024学年黑龙江省八年级上学期数学期末仿真模拟考试试卷

试卷更新日期：2023-12-20 类型：期末考试

进入出卷网下载

一、选择题

1. 下面四个图形分别是节能、节水、低碳和绿色食品标志，是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 如果一个三角形的两边长分别为2和5，则第三边长可能是（　　）

A、2 B、3 C、5 D、8

查看试题解析
3. 下列运算中，不正确的是（）

A、 $2 x^{2} - x^{2} = x^{2}$ B、 ${(- 2 x^{2})}^{3} = - 8 x^{6}$ C、 $x^{3} \cdot x^{2} = x^{5}$ D、 $x^{9} \div x^{3} = x^{3}$

查看试题解析
4. 如图，在由4个相同的小正方形拼成的网格中，∠2-∠1=（）

A、60° B、75° C、90° D、105°

查看试题解析
5. 下列各式不是分式的是（　　）

A、 $\frac{x}{y}$ B、 $\frac{3 x}{x + 1}$ C、 $\frac{x}{π}$ D、 $\frac{x - 1}{x}$

查看试题解析
6. 已知（x+m）（x-5）=x²-3x+k．则k，m的值分别是（）

A、k=10，m=2 B、k=10，m=-2 C、k=-10，m=-2 D、k=-10，m=2

查看试题解析
7. 如图，小明书上的三角形被墨迹遮挡了一部分，但他很快想到办法在作业本上画了一样的三角形，那么这两个三角形完全一样的依据是（）

A、AAS B、ASA C、SSS D、SAS

查看试题解析
8. 如图， $O P$ 平分 $∠ A O B$ ， $P A ⊥ O A$ ， $P B ⊥ O B$ ，垂足分别为A ， B ，下列结论中不一定成立的是（　　）

A、 $P A = P B$ B、 $P O$ 平分 $∠ A P B$ C、 $O A = O B$ D、 $A B$ 垂直平分 $O P$

查看试题解析
9. 师傅和徒弟两人每小时一共做40个零件，在相同的时间内，师傅做了300个零件，徒弟做了100个零件．师傅每小时做了多少个零件？若设师傅每小时做了x个零件，则可列方程为（　　）

A、 $\frac{300}{x} = \frac{100}{40 - x}$ B、 $\frac{300}{40 - x} = \frac{100}{x}$ C、 $\frac{300}{x} = \frac{100}{x - 40}$ D、 $\frac{300}{x - 40} = \frac{100}{x}$

查看试题解析
10. 若a²-b²=4，a-b=-2，则a+b的值为（）

A、2 B、1 C、-0.5 D、-2

查看试题解析

二、填空题

11. 长泾老街的“龙圆坊”在中秋月饼的销售中再创新高，总计销售了月饼865000个月饼，这个数据用科学记数法表示为 .

查看试题解析
12. 计算： ${(\sqrt{3} - 1)}^{0} + 2^{- 1} =$ ．

查看试题解析
13. 因式分解：3x³-12x= ．

查看试题解析
14. 分式 $\frac{| x | - 4}{x + 4}$ 值为0， $x =$ ．

查看试题解析
15. 不等式组 ${\begin{array}{l} 1 - 2 x < 3 \\ 3 x - 2 \leq 5 \end{array}$ 的整数解有个．

查看试题解析
16. 如图，已知△ABC≌△DBE，AB=5，BE=12，则CD的长为

查看试题解析
17. 如图，在△ABC 中，AB=AC，∠A=36°，BD是∠ABC的平分线．图中有个等腰三角形．

查看试题解析
18. 若等腰三角形的一个外角为150°，则它的底角为度．

查看试题解析
19. 若a^m= 4，a^2m+n= 128，则aⁿ=

查看试题解析
20. 如图，D为△ABC内一点，CD平分∠ACB，BE⊥CD，垂足为D，交AC于点E，若∠A =∠ABE，AC = 10，BC = 6，则BD的长为

查看试题解析

三、解答题

21. 先化简，再求值： $\frac{a + 1}{a - 2} \div (\frac{a}{a - 2} + \frac{1}{a^{2} - 4})$ ，请从－2，－1，1，2四个数中选择一个合适的数代入求值．

查看试题解析
22. 如图，△ABC三个顶点的坐标分别为A（-4，1），B（-3，3），C（-1，2）．
⑴作出△ABC关于y轴对称的△A′B′C′，并写出C′的坐标；
⑵求出△A′B′C′的面积；
⑶在x轴上画出点P ，使PA+PC最小，并写出点P的坐标．（不写作法，保留作图痕迹）

查看试题解析
23. 解放中学为了了解学生对新闻、体育、动画、娱乐四类电视节目的喜爱程度，随机抽取了部分学生进行调查(每人限选1项)，现将调查结果绘制成如下两幅不完整的统计图，根据图中所给的信息解答下列问题.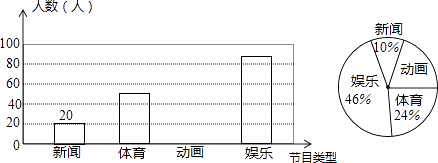

(1)、喜爱动画的学生人数和所占比例分别是多少？

(2)、请将条形统计图补充完整；

(3)、若该校共有学生1000人，依据以上图表估计该校喜欢体育的人数约为多少？

查看试题解析
24. 某超市预测某饮料有发展前途，用1600元购进一批饮料，面市后果然供不应求，又用6000元购进这批饮料，第二批饮料的数量是第一批的3倍，但单价比第一批贵2元。

(1)、第一批饮料进货单价多少元？

(2)、若二次购进饮料按同一价格销售，两批全部售完后，获利不少于1200元，那么销售单价至少为多少元？

查看试题解析
25. 如图，在△ABC中，AB=AC，点D，E，F分别在AB，BC，AC边上，且BE=CF，BD=CE.

(1)、求证：∠BDE=∠CEF；

(2)、当∠A=40°时，求∠DEF的度数.

查看试题解析
26. 已知关于x的方程 $\frac{2 x}{x - 2} + \frac{m}{x - 2} = - 2$

(1)、当 $m = 5$ 时，求方程的解；

(2)、当m取何值时，此方程无解；

(3)、当此方程的解是正数时，求m的取值范围．

查看试题解析
27. 如图，点C，E，F，B在同一直线上，点A，D在 $B C$ 异侧， $A B ∥ C D$ ， $B F = C E$ ， $∠ A = ∠ D$ .

(1)、求证： $A B = C D$ .

(2)、若 $A B = C F$ ，试判断 $△ C D F$ 的形状，并说明理由；

(3)、在（2）的条件下，若 $∠ B = 30 °$ ，求 $∠ D F B$ 的度数.

查看试题解析