（人教版）2023-2024学年八年级上学期数学 15.2 分式的运算期末复习(吉林地区专用)

试卷更新日期：2023-12-19 类型：复习试卷

进入出卷网下载

一、选择题

1. 下列等式，错误的是（　　）

A、5y³•3y⁵＝15y⁸ B、（﹣5a⁵b³c）÷（15a⁴b）＝﹣ $\frac{1}{3}$ ab²c C、（π﹣3）⁰＝1 D、（﹣xy）³＝﹣xy³

查看试题解析
2. 老师设计了接力游戏，用合作的方式完成分式化简，规则是：每人只能看到前一人给的式子，并进行一步计算，再将结果传递给下一人，最后完成化简．过程如图所示：
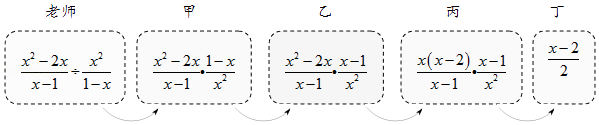
接力中，自己负责的一步出现错误的是（）

A、只有乙 B、甲和丁 C、乙和丙 D、乙和丁

查看试题解析
3. 化简 $\frac{a^{2}}{a - 1} - \frac{a}{a - 1}$ 的结果为（）

A、a B、 $a - 1$ C、 $\frac{a}{a - 1}$ D、 $a^{2} - a$

查看试题解析
4. 若 $x^{m} y^{n} \div x^{3} y = \frac{1}{x}$ ，则（）

A、m=6，n=1 B、m=4，n=1 C、m=2，n=1 D、m=2，n=0

查看试题解析
5. 若 ${(x - 1)}^{0} = 1$ 成立，则 $x$ 的取值范围是（）

A、 $x = - 1$ B、 $x \neq 1$ C、 $x = 1$ D、 $x \neq 0$

查看试题解析
6. 如果a＝﹣1² ， b＝（3﹣π）⁰ ， c＝（﹣0.25）²⁰²³×4²⁰²⁴ ，那么a ， b ， c的大小关系为（　　）

A、a＝b＞c B、b＞a＞c C、c＞b＝a D、c＞a＞b

查看试题解析
7. 试卷上一个正确的式子（ $\frac{1}{a - b} - \frac{1}{a + b}$ ）÷＝ $\frac{2}{a + b}$ 被莹莹不小心滴上墨汁，被墨汁遮住的部分的代数式是（）

A、 $\frac{a}{a - b}$ B、 $\frac{a}{a + b}$ C、 $\frac{b}{a + b}$ D、 $\frac{b}{a - b}$

查看试题解析
8. 实数m，n在数轴上的对应点的位置如图所示，则下列不等关系成立的是（　　）

A、n<m B、n²<m² C、n⁰<m⁰ D、|n|<|m|

查看试题解析

二、填空题

9. 计算： $3^{0} =$ .

查看试题解析
10. 若（a-2023）⁰=1，则a的取值范围是

查看试题解析
11. 已知 $x_{1} ， x_{2} ， x_{3} ， \cdot \cdot \cdot x_{20}$ 都是不等于0的有理数，若 $y_{1} = \frac{| x_{1} |}{x_{1}}$ ，则 $y_{1}$ 等于1或 $- 1$ ；若 $y_{2} = \frac{| x_{1} |}{x_{1}} + \frac{| x_{2} |}{x_{2}}$ ，则 $y_{2}$ 等于2或 $- 2$ 或0；若 $y_{20} = \frac{| x_{1} |}{x_{1}} + \frac{| x_{2} |}{x_{2}} + \frac{| x_{3} |}{x_{3}} + \cdot \cdot \cdot + \frac{| x_{20} |}{x_{20}}$ ，则 $y_{20}$ 所有可能等于的值的绝对值之和等于．

查看试题解析
12. 如果（x-3）^x=1，则x的值为

查看试题解析
13. 化简 $\frac{a^{2} b}{a^{2} - a b} \cdot (\frac{a}{b} - \frac{b}{a})$ 的结果是．

查看试题解析
14. 已知 $x$ ， $y$ ， $z$ ， $a$ ， $b$ 均为非零实数，且满足 $\frac{x y}{x + y} = \frac{1}{a^{3} - b^{3}} ， \frac{y z}{y + z} = \frac{1}{a^{3}} ， \frac{x z}{x + z} = \frac{1}{a^{3} + b^{3}} ， \frac{x y z}{x y + y z + z x} = \frac{2}{81}$ ，则 $a$ 的值为．

查看试题解析

三、解答题

15. 先化简： $\frac{x^{2} + x - 6}{x} \div \frac{x + 3}{x^{2} - 2 x}$ ，再求当 $x = 2 + \sqrt{3}$ 时代数式的值．

查看试题解析
16. 已知 $a = \frac{1}{\sqrt{3} + 2}$ ，求 $\frac{a^{2} + a - 6}{a^{2} - 4 a + 4}$ 的值.

查看试题解析
17. 已知： $a > 0$ ， $b > 0$ ， $\frac{a}{b} + \frac{b}{a} + 2 = a b$ ，且 $a \neq b$ .

(1)、求证： $a + b = a b$ ；

(2)、求 $\frac{a^{2}}{2 a - 2 b} - \frac{a^{2}}{2 a + 2 b} - \frac{a b^{2} + a^{2} b}{2 a^{2} - 2 b^{2}}$ 的值.

查看试题解析
18. 设不全相等的非零实数a，b，c满足 $\frac{b c}{2 a^{2} + b c} + \frac{a c}{2 b^{2} + a c} + \frac{a b}{2 c^{2} + a b}$ ＝1，求a+b+c的值．

查看试题解析
19. 已知 $A = (\frac{2 x^{2} + 2 x}{x^{2} - 1} - \frac{x^{2} - x}{x^{2} - 2 x + 1}) \div \frac{x}{x + 1}$ ．

(1)、先化简A ，再从1，2，3中选取一个合适的数作为x的值代入求值；

(2)、判断A的值能不能是 $- 1$ ，并说明理由．

查看试题解析
20. 研究表明，眼睛如果长时间不眨，眼液分泌量就会减少，导致眼睛干涩，易疲劳．据统计，人在玩手机或者电脑游戏时平均每分钟眨眼10次，比正常状态下每分钟眨眼的次数少二，人在正常状态下平均每分钟眨眼多少次?

查看试题解析
21. 根据规划设计，某工程队准备修建一条长 $1000 m$ 的公路 $.$ 由于采取新的施工方式，实际每天修建公路的长度比原计划增加 $20 m$ ，从而缩短了工期 $.$ 假设原计划每天修建公路a $m$ ，那么

(1)、原计划修建这条公路需要多少天？实际修建这条公路用了多少天？

(2)、实际修建这条公路的工期比原计划缩短了几天？

查看试题解析
22.

(1)、计算： $\sqrt{9} - (- 2023)^{0} + 2^{- 1}$ ；

(2)、以下是欣欣解方程： $\frac{x + 2}{3} - \frac{2 x - 1}{2} = 1$ 的解答过程：
解：去分母，得 $2 (x + 2) - 3 (2 x - 1) = 1$ ； $\dots ①$
去括号： $2 x + 2 - 6 x + 3 = 1$ ； $\dots ②$
移项，合并同类项得： $- 4 x = - 4$ ； $\dots ③$
解得： $x = 1 . \dots ④$
欣欣的解答过程在第步开始出错？请你完成正确的解答过程．

查看试题解析
23. 化简 $(\frac{x}{x + 1} + \frac{x}{x - 1}) \cdot \frac{x^{2} - 1}{x}$ ，下面是甲、乙两同学的部分运算过程：
甲同学：解：原式 $= [\frac{x (x - 1)}{(x + 1) (x - 1)} + \frac{x (x + 1)}{(x - 1) (x + 1)}] \cdot \frac{x^{2} - 1}{x} \dots$ ；

乙同学：解：原式 $= \frac{x}{x + 1} \cdot \frac{x^{2} - 1}{x} + \frac{x}{x - 1} \cdot \frac{x^{2} - 1}{x} \dots .$

(1)、甲同学解法的依据是，乙同学解法的依据是； $($ 填序号 $)$
      $①$ 等式的基本性质；
      $②$ 分式的基本性质；
      $③$ 乘法分配律；
      $④$ 乘法交换律．

(2)、请从甲、乙同学的解法中选择一种，写出完整的化简过程，然后从 $- 2$ ， $- 1$ ， $0$ ， $1$ ， $2$ 中挑选一个合适的数代入求值．

查看试题解析
24. 已知关于x ， y的方程组 ${\begin{cases} x + y = 3 m + 1 \\ 2 x - y = 8 - 6 n \end{cases}$ （m ， n为实数）．

(1)、若m+4n＝5，试探究方程组的解x ， y之间的关系；

(2)、若方程组的解满足2x+3y＝0，求分式 $\frac{4 m n + m^{2}}{m^{2} - 2 m n}$ 的值．

查看试题解析

（人教版）2023-2024学年八年级上学期数学 15.2 分式的运算 期末复习(吉林地区专用)

一、选择题

二、填空题

三、解答题

（人教版）2023-2024学年八年级上学期数学 15.2 分式的运算期末复习(吉林地区专用)