（人教版）2023-2024学年八年级上学期数学 14.2 乘法公式期末复习(吉林地区专用)

试卷更新日期：2023-12-19 类型：复习试卷

进入出卷网下载

一、选择题

1. 下列代数式添括号正确的是（）

A、a+b+2=a+(b-2) B、a-b-1=a-(b-1) C、a+b-1=a+(b+1) D、a-b+1=a-(b-1)

查看试题解析
2. 若k为任意整数，则（2k+3）²-4k²的值总能（）

A、被2整除． B、被3整除． C、被5整除． D、被7整除．

查看试题解析
3. 国际数学家大会是数学界的最高水平盛典，大合邀请著名数学粽子者，交流报告数学最新迸展和成果，由承办国的国泉元曾颁发世界数学最高奖——菲尔兹奖.2002年在北京召开了国数学家大会，会标图案是我国古代著名的”赵爽弦图”．图中包合四个面积为24的全等的直角三角形，围成的大正方形面积为100．则直角三角形中较长直角边与较短直角边的长度差为（）

A、2 B、4 C、6 D、8

查看试题解析
4. 若a²-b²=4，a-b=-2，则a+b的值为（）

A、2 B、1 C、-0.5 D、-2

查看试题解析
5. 已知x²+2mx+16（m为常数）是一个完全平方式，则m的值为（）

A、4． B、-4． C、±4． D、±8．

查看试题解析
6. 如图，在边长为a的正方形中挖掉一个边长为b的小正方形（a＞b），把余下的部分剪拼成一个矩形，验证了一个等式，则这个等式是（　　）

A、a²-ab＝a（a-b） B、（a+b）²＝a²+2ab+b² C、（a-b）²＝a²-2ab+b² D、a²-b²＝（a+b）（a-b）

查看试题解析
7. 已知(2021-a) (2020-a) =4，则(2021-a)²+ (2020-a)²的值为（）

A、9 B、8 C、7 D、12

查看试题解析
8. 如图，在边长分别为a，b的两个正方形组成的图形中，剪去一个边长为（a-b）的正方形，通过用两种不同的方法计算剪去的正方形的面积，可以验证的乘法公式是（）

A、 $a (a + b) = a^{2} + a b$ B、 $(a + b) (a - b) = a^{2} - b^{2}$ C、 $(a + b)^{2} = a^{2} + 2 a b + b^{2}$ D、 $(a - b)^{2} = a^{2} - 2 a b + b^{2}$

查看试题解析

二、填空题

9. 已知a+b=3，ab=1，则a²-ab+b²= ．

查看试题解析
10. 若要使4x²+mx+ $\frac{1}{64}$ 成为一个两数差的完全平方式，则m的值应为

查看试题解析
11. 若 m+n=2，n-m =-3，则 $n^{2} - m^{2} =$ .

查看试题解析
12. 若代数式x²-8x+m是关于x的完全平方式。则实数m= ．

查看试题解析
13. 从边长为a的正方形中减掉一个边长为b的正方形（如图1）．然后将剩余部分拼成一个长方形（如图2），上述操作能验证的等式是

查看试题解析
14. 若x²- 2mx+25是一个完全平方式，则m的值为

查看试题解析

三、解答题

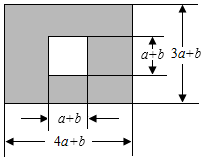
15. 已知（x+y）²＝1，（x-y）²＝49，求x²+y²与xy的值．

查看试题解析
16. 如图，某中学校园内有一个长为（4a+b）米，宽为（3a+b）米的长方形小广场，
学校计划在中间留一块边长为（a+b）米的正方形场地修建一座雕像，并将空余场地（阴影部分）进行绿化．求绿化的面积．（用含a、b的代数式表示）

查看试题解析
17. 如图，在一张半径为R的圆形钢板上，挖去半径均为r的四个小圆．计算当 $R = 7.8 c m$ ， $r = 1.1 c m$ 时剩余部分的面积（ $π$ 取3）．

查看试题解析
18. 先化简，再求值：x(3-x)+(x+1)(x-1)，其中x= $- \frac{1}{3}$

查看试题解析
19. 在解决问题“已知 $a = \frac{1}{\sqrt{2} - 1}$ ，求 $3 a^{2} - 6 a - 1$ 的值”时，小明是这样分析与解答的：
$∵ a = \frac{1}{\sqrt{2} - 1} = \frac{\sqrt{2} + 1}{(\sqrt{2} - 1) (\sqrt{2} + 1)} = \sqrt{2} + 1$ ，

$∴ a - 1 = \sqrt{2}$ ，

$∴ {(a - 1)}^{2} = 2 ， a^{2} - 2 a + 1 = 2$

$∴ a^{2} - 2 a = 1$

$∴ 3 a^{2} - 6 a = 3 ， 3 a^{2} - 6 a - 1 = 2$

请你根据小明的分析过程，解决如下问题：

若 $a = \frac{2}{3 - \sqrt{7}}$ ，求 $2 a^{2} - 12 a + 1$ 的值．

查看试题解析
20.
如图：某校一块长为2a米的正方形空地是七年级四个班的清洁区，其中分给七年级（1）班的清洁区是一块边长为（a﹣2b）米的正方形，（0＜b＜ $\frac{a}{2}$ ），
（1）分别求出七（2）、七（3）班的清洁区的面积；
（2）七（4）班的清洁区的面积比七（1）班的清洁区的面积多多少平方米？

查看试题解析
21. 图①是由边长分别为a，b （a>b）的两个正方形拼成的图形，其面积为S₁ ，图②是长、宽分别为a，b的长方形。其面积为S₂ ．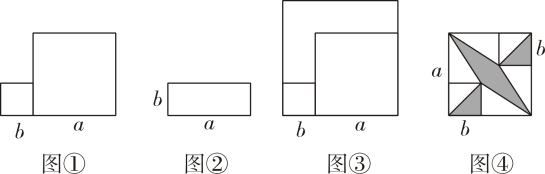

(1)、图③是由图①中的图形补成的大正方形。其面积为S₃ ．则S₁、S₂ ， S₃的数量关系是

(2)、对于图③，通过两种不同方法计算它的面积，可以得到一个代数恒等式是：

(3)、在图①边长为a的正方形中放入两个边长为b的小正方形。得到图④所示的图形．若S₁=16，S₂=5，求图④中阴影部分的面积．

查看试题解析
22. 对于一个图形，通过不同的方法计算图形的面积，就可以得到一个数学等式．

(1)、模拟练习，如图，写出一个我们熟悉的数学公式：．

(2)、解决问题：如果 $a + b = 10$ ， $a b = 16$ ，求 $a^{2} + b^{2}$ 的值；

(3)、类比探究：如果一个长方形的长和宽分别为 $(8 - x)$ 和 $(x - 2)$ ，且 ${(8 - x)}^{2} + {(x - 2)}^{2} = 22$ ，求这个长方形的面积．

查看试题解析
23. “筑牢民生之基，增强百姓幸福感”，沙坪坝区如火如荼地进行着社区环境的改善，提升老百姓的生活品质 $.$ 如图，某小区内有一块长为 $(3 a - b)$ 米，宽为 $(2 a + b)$ 米的长方形地块，小区计划在中间留一块边长为 $(a + b)$ 米的正方形地块修建一座假山，然后将剩余阴影部分进行绿化．

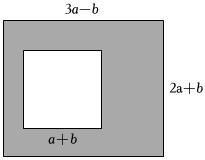(1)、求绿化部分的面积 $($ 用含 $a$ ， $b$ 的代数式表示 $)$ ；

(2)、当 $a = 3$ ， $b = 1$ 时，求绿化部分的面积．

查看试题解析
24. 为创建文明校园环境，高校长制作了“节约用水”“讲文明，讲卫生”等宣传标语，标语由如图 $①$ 所示的板材裁剪而成，其为一个长为 $2 m$ ，宽为 $2 n$ 的长方形板材，将长方形板材沿图中虚线剪成四个形状和大小完全相同的小长方形标语，在粘贴过程中，同学们发现标语可以拼成图 $②$ 所示的一个大正方形．

(1)、用两种不同方法表示图 $②$ 中小正方形 $($ 阴影部分 $)$ 面积：
方法一： $S_{小正方形} =$ ；
方法二： $S_{小正方形} =$ ；

(2)、 $(m + n)^{2}$ ， $(m - n)^{2}$ ， $4 m n$ 这三个代数式之间的等量关系为；

(3)、根据 $(2)$ 题中的等量关系，解决如下问题：
$①$ 已知： $a - b = 5$ ， $a b = - 6$ ，求： $(a + b)^{2}$ 的值；
$②$ 已知： $a - \frac{1}{a} = 1$ ，求： $(a + \frac{1}{a})^{2}$ 的值．

查看试题解析

（人教版）2023-2024学年八年级上学期数学 14.2 乘法公式 期末复习(吉林地区专用)

一、选择题

二、填空题

三、解答题

（人教版）2023-2024学年八年级上学期数学 14.2 乘法公式期末复习(吉林地区专用)