(人教版)2023-2024学年八年级上学期数学 13.4 课题学习 最短路径问题 期末复习(吉林地区专用)
试卷更新日期:2023-12-19 类型:复习试卷
一、选择题
-
1. 如图,在正方形网格中有M,N两点,在直线l上求一点P,使PM+PN最短, 则点P应选在( )
 A、A点 B、B点 C、C点 D、D点2. 如下图,直线L是一条河,P,Q是两个村庄.欲在L上的某处修建一个水泵站M,向P,Q两地供水,现有如下四种铺设方案,图中实线表示铺设的管道,则所需管道最短的是( ).A、
A、A点 B、B点 C、C点 D、D点2. 如下图,直线L是一条河,P,Q是两个村庄.欲在L上的某处修建一个水泵站M,向P,Q两地供水,现有如下四种铺设方案,图中实线表示铺设的管道,则所需管道最短的是( ).A、 B、
B、 C、
C、 D、
D、 3. 如图,直线是线段AB的垂直平分线,点C在直线外,且与A点在直线的同一侧,点P是直线上的任意点,连接AP,BC,CP,则BC与AP+PC的大小关系是( )
3. 如图,直线是线段AB的垂直平分线,点C在直线外,且与A点在直线的同一侧,点P是直线上的任意点,连接AP,BC,CP,则BC与AP+PC的大小关系是( ) A、> B、< C、≥ D、≤4. 如图, 中, ,将 沿DE翻折,使得点A落在平面内的 处,若 ,则 的度数是( )
A、> B、< C、≥ D、≤4. 如图, 中, ,将 沿DE翻折,使得点A落在平面内的 处,若 ,则 的度数是( ) A、 B、 C、 D、5. 如图, ,点 是 内的一定点,点 分别在 上移动,当 的周长最小时, 的值为( )
A、 B、 C、 D、5. 如图, ,点 是 内的一定点,点 分别在 上移动,当 的周长最小时, 的值为( ) A、 B、 C、 D、6. 如图,在半圆O中,直径AB=4,点C、D是半圆上的两点,且∠BOC=84°,∠BOD=36°,P为直径AB上一点,则PC+PD的最小值为( )
A、 B、 C、 D、6. 如图,在半圆O中,直径AB=4,点C、D是半圆上的两点,且∠BOC=84°,∠BOD=36°,P为直径AB上一点,则PC+PD的最小值为( )
A、4 B、2 C、2 D、27. 如图,∠AOB=30°,∠AOB 内有一定点 P,且 OP=12,在 OA 上有一动点 Q,OB 上有 一动点 R。若△PQR 周长最小,则最小周长是( )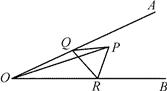 A、6 B、12 C、16 D、208. 如图,在锐角△ABC中,AC=10,S△ABC =25,∠BAC的平分线交BC于点D,点M,N分别是AD和AB上的动点,则BM+MN的最小值是( )
A、6 B、12 C、16 D、208. 如图,在锐角△ABC中,AC=10,S△ABC =25,∠BAC的平分线交BC于点D,点M,N分别是AD和AB上的动点,则BM+MN的最小值是( ) A、4 B、 C、5 D、6
A、4 B、 C、5 D、6二、填空题
-
9. 如图,在△ABC中,AB=5,AC=7,MN为BC边的垂直平分线,若点D在直线MN上,连接AD、BD,则△ABD周长的最小值为 .
 10. 如图,中, , , , , 平分 , 如果点P,点Q分别为 , 上的动点,那么的最小值是 .
10. 如图,中, , , , , 平分 , 如果点P,点Q分别为 , 上的动点,那么的最小值是 . 11. 如图,等边三角形ABC的边长为4,AD是BC边上的中线,F是AD边上的动点,E是边AC的中点.当△ECF的周长取得最小值时,∠EFC的度数为 .
11. 如图,等边三角形ABC的边长为4,AD是BC边上的中线,F是AD边上的动点,E是边AC的中点.当△ECF的周长取得最小值时,∠EFC的度数为 . 12. 如图,在中, , . 为边上的垂直平分线,若点D在直线上,连接 , , 则周长的最小值为 .
12. 如图,在中, , . 为边上的垂直平分线,若点D在直线上,连接 , , 则周长的最小值为 .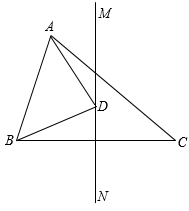 13. 如图,是等边三角形,是边上的高,是的中点,是上的一个动点,当与的和最小时,度.
13. 如图,是等边三角形,是边上的高,是的中点,是上的一个动点,当与的和最小时,度.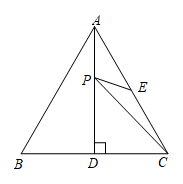 14. 如图,在△ABC中,AB=AC=10,BC=12,AD=8,AD是∠BAC的平分线.若P,Q分别是AD和AC上的动点,则PC+PQ的最小值是 .
14. 如图,在△ABC中,AB=AC=10,BC=12,AD=8,AD是∠BAC的平分线.若P,Q分别是AD和AC上的动点,则PC+PQ的最小值是 .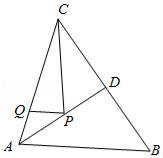
三、解答题
-
15. 如图,亮亮在A处看护羊群吃草,其家在B处,A,B到河岸的距离分别为AC=200m,BD=100m,CD=400m,亮亮从A处把羊群赶到河边饮水后回家,作图说明亮亮如何行走路程最短,并求出亮亮走的最短路程.
 16. 已知:如图,点M在锐角∠AOB的内部,在OA边上求作一点P , 在OB边上求作一点Q , 使得△PMQ的周长最小.
16. 已知:如图,点M在锐角∠AOB的内部,在OA边上求作一点P , 在OB边上求作一点Q , 使得△PMQ的周长最小. 17. 如图,等边 的边长为 , 是 边上的中线, 是 边上的动点, 是 边上一点,若 ,当 取得最小值时,则 的度数为多少?
17. 如图,等边 的边长为 , 是 边上的中线, 是 边上的动点, 是 边上一点,若 ,当 取得最小值时,则 的度数为多少? 18. 如图所示, 内有一点 ,点 到点 的距离为 在 边上各取一点 使 的周长最小并求出这个最小值.(保留作图痕迹并说明结果)
18. 如图所示, 内有一点 ,点 到点 的距离为 在 边上各取一点 使 的周长最小并求出这个最小值.(保留作图痕迹并说明结果)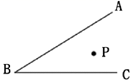 19. 点P、P1关于OA对称,P、P2关于OB对称,P1P2交OA、OB于M、N,若P1P2=8,则△MPN的周长是多少?
19. 点P、P1关于OA对称,P、P2关于OB对称,P1P2交OA、OB于M、N,若P1P2=8,则△MPN的周长是多少? 20. 如图,一个牧童在小河的南2km的A处牧马,而他正位于他的小屋B的西 km北3km处,他想把他的马牵到小河边去饮水,然后回家.他要完成这件事情所走的最短路程是多少?
20. 如图,一个牧童在小河的南2km的A处牧马,而他正位于他的小屋B的西 km北3km处,他想把他的马牵到小河边去饮水,然后回家.他要完成这件事情所走的最短路程是多少? 21. 如图,∠AOB=30°,角内有一点P,PO=10cm,两边上各有一点Q,R(均不同于点O),则△PQR的周长的最小值是多少?
21. 如图,∠AOB=30°,角内有一点P,PO=10cm,两边上各有一点Q,R(均不同于点O),则△PQR的周长的最小值是多少?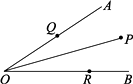 22. 如图
22. 如图 (1)、如图,已知△ABC,请你作出AB边上的高CD,AC边上的中线BE,角平分线AF(不写作法,保留痕迹)(2)、如图,直线l表示一条公路,点A,点B表示两个村庄.现要在公路上造一个车站,并使车站到两个村庄A,B的距离之和最短,问车站建在何处?请在图上标明地点,并说明理由.(要求尺规作图,不写作法)23. 如图,∠AOB=30°,点P是∠AOB内一点,PO=8,在∠AOB的两边分别有点R、Q(均不同于O),求△PQR周长的最小值.
(1)、如图,已知△ABC,请你作出AB边上的高CD,AC边上的中线BE,角平分线AF(不写作法,保留痕迹)(2)、如图,直线l表示一条公路,点A,点B表示两个村庄.现要在公路上造一个车站,并使车站到两个村庄A,B的距离之和最短,问车站建在何处?请在图上标明地点,并说明理由.(要求尺规作图,不写作法)23. 如图,∠AOB=30°,点P是∠AOB内一点,PO=8,在∠AOB的两边分别有点R、Q(均不同于O),求△PQR周长的最小值. 24. 如图,在平面直角坐标系中,一次函数y=x的图象为直线l.
24. 如图,在平面直角坐标系中,一次函数y=x的图象为直线l. (1)、观察与探究
(1)、观察与探究已知点A与A′,点B与B′分别关于直线l对称,其位置和坐标如图所示.请在图中标出C(4,﹣1)关于线l的对称点C′的位置,并写出C′的坐标
(2)、归纳与发现观察以上三组对称点的坐标,你会发现:
平面直角坐标系中点P(a,b)关于直线l的对称点P′的坐标为;
(3)、运用与拓展已知两点M(﹣3,3)、N(﹣4,﹣1),试在直线l上作出点Q,使点Q到M、N两点的距离之和最小,并求出相应的最小值.