（人教版）2023-2024学年八年级上学期数学 13.3 等腰三角形 期末复习(吉林地区专用)
试卷更新日期：2023-12-19 类型：复习试卷
一、选择题
-
1. 等腰三角形一边长9cm，另一边长4cm， 它的第三边是（ ） cm．A、4 B、9 C、4或9 D、不能确定2. 如图，EC、BD是正五边形ABCDE的对角线，则∠1的大小为（ ）
A、72° B、75° C、60° D、80°3. 一个等腰三角形的顶角是120°．则它的底角度数是（ ）A、30° B、60° C、40° D、不能确定。4. 如图，在△ABC中，以点A为圆心、AC长为半径作圆弧交BC于点D，再分别以点B和点D为圆心。大于BD长为半径作圆弧，两弧分别交于点M和点N．连结MN交AB于点E，若△MDE的周长为13．AC=5，则AB的长为（ ）
A、4 B、8 C、9 D、105. 如图，在△ABC中，AB=AC，∠B=52°，以点C为圆心，CA长为半径作弧交AB于点D，分别以点A和点D为圆心，大于AD的长为半径作弧，两弧相交于点E，作直线CE交AB于点F，则∠ACF的度数是（ ）
A、24° B、26° C、14° D、18°6. 如图，在△ABC中，AB=AC，∠B=30°，D为BC上一点，若CD=AD=4，则BC的长为（ ）
A、10 B、12 C、14 D、167. 如图，△ABC中，∠C＝90°， AB=4， ∠B＝30°，点P是BC边上的动点，则AP长不可能是（ ）
A、1.8 B、2.2 C、3.5 D、3.88. 如图，在△ABC中，AB＝BC， ∠BAC=120°， AB的垂直平分线交AB于点E，交BC于点F， 若BF=2， 则CF的长为（ ）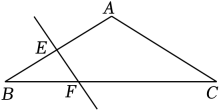
A、2 B、4 C、6 D、8二、填空题
-
9. 等腰三角形的周长为20cm，一边长为6cm，则底边长为 cm．
10. 已知两根长度分别为3cm.7cm的木伟，若想钉一个等腰下角形木架，第三根木棒的长度应该是 cm．11. 如图，△ABC是等边三角形，AD∥BC，CD⊥AD．若AD =2cm，则AB=cm．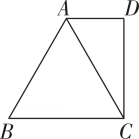
12. 如图，等边△ABC的顶点A（-4，0），顶点C在y轴上．则点B的坐标是
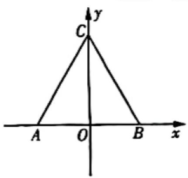13. 如图，△ABC是等边三角形，直线l过顶点B，作点C关于直线l的对称点D，连接BD，AD，CD，若∠BAD=25°，则∠BCD的度数为
14. 若等腰三角形的一边长为3，另一边长为7，则这个三角形的周长为三、解答题
-
15.
如图，在△ABC中，AB=AC，点D在AC上，且BD=BC=AD，求△ABC各角的度数．
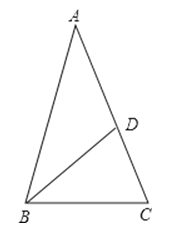16. 如图．在△ABC中，AD平分2 BAC交BC于点D，DF⊥AD交AB于点F，若∠B= 25°，∠C= 75° ，求证：△BFD是等腰三角形．
17. 如图，△ABC中，AB=AC，点D在BC边上，连接AD，若AD=BD，AC=DC，求∠DAC的度数．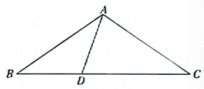
18. 如图，AB = BC，∠CDE =120°，DF ∥BA，且 DF 平分∠CDE，求证：是等边三角形.
19. 如图，在中， ， 斜边AB 的垂直平分线交AC于点E，交AB于点 D，AE = 8cm，求 BC 的长.
20. 如图，点C在线段AB上， ， ， .求证：为等腰三角形
21. 如图，在中，于点D.
(1)、求证：(2)、若 AF 平分分别交CD、BC于 点E、F，求证：是等腰三角形.22. 如图，在△ABC中，∠ABC的平分线交AC于点D，过点D作DE∥BC交AB于点E．
(1)、求证：BE=DE；(2)、若∠A=75°，∠C=36°，求∠BDE的度数．23. 如图，△ABC是等边三角形．
(1)、 如图①，DE∥BC，分别交AB、AC于点D、E．求证：△ADE是等边三角形；(2)、如图②，△ADE仍是等边三角形，点B在ED的延长线上，连接CE，判断∠BEC的度数及线段AE、BE、CE之间的数量关系，并说明理由．24. 在边长为9cm的等边三角形ABC中，点Q是BC边上的一点，动点P以1cm/s的速度从点A沿AB向点B运动，设运动时间为t（s）．
(1)、如图①，若BQ=6，PQ∥AC，求t的值；(2)、如图②，若点P从点A向点B运动的同时，点Q以2cm/s的速度从点B沿BC-CA向点A运动，求t为何值时，OAPQ是等边三角形；(3)、如图③，将边长为9cm的等边三角形ABC变换为以AB、AC为腰、BC为底的等腰三角形，且AB=AC=10cm，BC=8cm，点P运动到AB的中点处停止．点P停止运动后，点M以1cm/s的速度从点B沿BC向点C运动，同时点N以acm/s的速度从点C沿CA向点A运动，当△BPM与△CNM全等时，直接写出a的值．