（人教版）2023-2024学年八年级上学期数学 12.3 角的平分线的性质期末复习(吉林地区专用)

试卷更新日期：2023-12-19 类型：复习试卷

进入出卷网下载

一、选择题

1. 如图，在△ABC中，∠C=90°，∠CAB=50°．按以下步骤作图：①以点A为圆心，小于AC长为半径画弧，分别交AB、AC于点E月；②分别以点E F为圆心，大于 $\frac{1}{2}$ EF长为半径画弧，两弧相交于点G；③作射线AG交边BC于点D．则∠ADC的度数为（）

A、65° B、60° C、55° D、45°

查看试题解析
2. 如图，AD 是△ABC中∠BAC的平分线，DE⊥AB于点E，△ABC的面积为12，DE =2，AB = 7，则 AC 的长是（）

A、3 B、4 C、5 D、6

查看试题解析
3. 如图，在△ABC中，AD是△ABC的角平分线， DE⊥AC，若∠B＝40°，∠C＝60°，则∠ADE的度数为（）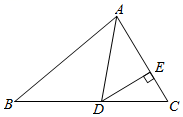

A、30° B、40° C、50° D、60°

查看试题解析
4. 如图，在△ABC中，∠C=90°．用直尺和圆规在边BC上确定一点P，使点P到点A、点B的距离相等，则符合要求的作图痕迹是（　　）

A、 B、 C、 D、

查看试题解析
5. 如图， $△ A B C$ 中， $∠ C = 90 °$ ， $A D$ 平分 $∠ B A C$ ， $A B = 10$ ， $C D = 3$ ，则 $△ A B D$ 的面积为（　　）

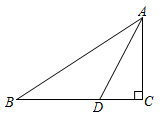A、20 B、10 C、15 D、30

查看试题解析
6. 如图，在Rt△ABC中，∠C=90°，以顶点B为圆心，适当长度为半径画弧，分别交AB、BC于点M、N，再分别以点M、N为圆心，大于 $\frac{1}{2}$ MN的长为半径画弧，两弧交于点P，作射线BP交边AC于点D．若CD=2 $\sqrt{3}$ ， AB=12，则△ABD的面积为（）

A、6 $\sqrt{3}$ B、12 $\sqrt{3}$ C、18 $\sqrt{3}$ D、24 $\sqrt{3}$

查看试题解析
7. 如图，在Rt△ABC中，∠ACB=90°，∠BAC=30°，∠ACB的平分线与∠ABC的外角的平分线交于E点，连接AE，则∠AEC的度数是（）

A、45° B、40° C、35° D、30°

查看试题解析
8. 如图，直线AB∥CD，直线EF分别与AB，CD相交于点E，F，∠BEF的平分线EN与CD相交于点N。若∠1=65°，则∠2=（）

A、64° B、50° C、60° D、54°

查看试题解析

二、填空题

9. 如图．四边形ABCD中．∠B=∠C=90°．AM、DM分别是∠DAB与∠ADC的平分线．AD=10．BC=6．则△ADM的面积为

查看试题解析
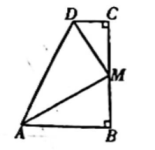10. 如图，△ABC中，BD是∠ABC的平分线，DE⊥AB于点E，S_△A_BC= $\frac{25}{2}$ ， AB=6，BC=4，那么DE=

查看试题解析
11. 如图，在Rt△BC中，∠C=90°。以顶点B为圆心、BC长为半径作圆弧，交AB于点D，再分别以点C和点D为圆心、大于 $\frac{1}{2}$ CD长为半径作圆弧，两弧交于点E．作射线BE交AC于点F．若BC=12，AB=15，△BCF的面积为24．则△ABC的面积为

查看试题解析
12. 如图，Rt△ABC中，∠C=90°，BD平分∠ABC交AC于点D，点E为AB的中点，若AB=12，CD=3，则△DBE的面积为

查看试题解析
13. 如图，在Rt△ABC中，∠ACB=90°，BD平分∠ABC，DE⊥AB于点E，AC=9，AD=5，则DE的长为．

查看试题解析
14. 两把相同的长方形直尺按如图所示方式摆放，记两把直尺的接触点为P ，其中一把直尺边缘和射线 $O A$ 重合，另一把直尺的下边缘与射线 $O B$ 重合，连接 $O P$ 并延长，若 $∠ B O P = 28 °$ ，则 $∠ A O B$ 的度数为．

查看试题解析

三、解答题

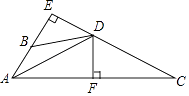
15. 如图，已知DE⊥AB，垂足为E，DF⊥AC，垂足为F，若AE=CF，DA=DC．
求证：AD是∠BAC的平分线．

查看试题解析
16. 如图，在△ABC中，∠B=30°，∠C=50°，∠BAC的平分线AD交BC于点D．求∠DAC与∠ADB的度数．

查看试题解析
17. 已知：在等腰 $R t △ A B C$ 中， $A C = B C$ ， $∠ C = 90 °$ ， AD平分 $∠ B A C$ ， $D E ⊥ A B$ 于点E，求证： $B D + D E = A C$ ．

查看试题解析
18. 在 $△ A B C$ 中， $∠ A = 90 °$ ， BD平分 $∠ A B C$ ， $A D = 3$ ， $B C = 10$ ， $△ A B C$ 的面积为27．求AB的长．

查看试题解析
19. 如图，在 $△ A B C$ 中， $∠ C = 30 °$ ， $∠ B = 58 °$ ， $A D$ 平分 $∠ C A B$ 交 $B C$ 于 $D$ ．求 $∠ C A D$ 和 $∠ 1$ 的度数．

查看试题解析
20. 如图，OC是∠AOB内的一条射线，D是OC上一点，过点D作DE⊥OA于点E， DF⊥OB于点F，已知OE＝OF ，求证：OC是∠AOB的平分线．

查看试题解析
21. 已知：如图，在 $R t △ A B C$ 中， $∠ C = 90 °$ ， $A D$ 是 $△ A B C$ 的角平分线， $D E ⊥ A B$ ，垂足为点 $E$ ， $A E = B E$ ．

(1)、求 $∠ B$ 的度数．

(2)、如果 $A C = 3$ cm， $C D = 2$ cm，求 $△ A B D$ 的面积．

查看试题解析
22. 在△ABC和△ADE中，AB=AD，AC=AE，∠BAC=∠DAE．

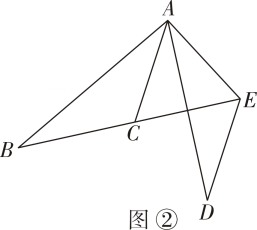(1)、如图①，求证：∠ABC=∠ADE；

(2)、如图②，若AD平分∠CAE，∠DAE=30°，点C在线段BE上，则∠D=度．

查看试题解析
23. 如图，△ABC中，AD是△ABC的角平分线，DE⊥AB于点E．

(1)、若∠B＝40°，∠C＝76°，求∠EDA的度数．

(2)、若AB＝20，AC＝16，DE＝6，求△ABC的面积．

查看试题解析
24. 如图， $△ A B C$ 中， $∠ A B C$ 的角平分线与外角 $∠ A C D$ 的平分线交于 $A_{1}$ ．

(1)、如图 $1$ ，若 $∠ A = 70 °$ ，则 $∠ A_{1} =$ ．

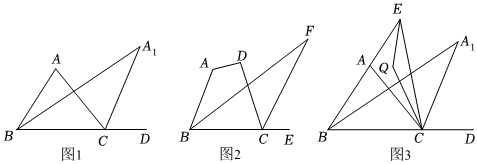(2)、如图 $2$ ，四边形 $A B C D$ 中， $∠ A B C$ 的角平分线及外角 $∠ D C E$ 的角平分线相交于点 $F$ ，若 $∠ A + ∠ D = 230 °$ ，求 $∠ F$ 的度数．

(3)、如图 $3$ ， $△ A B C$ 中， $∠ A B C$ 的角平分线与外角 $∠ A C D$ 的角平分线交于 $A_{1}$ ，若 $E$ 为 $B A$ 延长线上一动点，连接 $E C$ ， $∠ A E C$ 与 $∠ A C E$ 的角平分线交于点 $Q$ ，当 $E$ 滑动时有下面两个结论：
$① ∠ Q + ∠ A_{1}$ 的值为定值；

$② ∠ Q - ∠ A_{1}$ 的值为定值；

其中有且只有一个是正确的，请写出正确的结论，并求出其值．

查看试题解析

（人教版）2023-2024学年八年级上学期数学 12.3 角的平分线的性质 期末复习(吉林地区专用)

一、选择题

二、填空题

三、解答题

（人教版）2023-2024学年八年级上学期数学 12.3 角的平分线的性质期末复习(吉林地区专用)