（人教版）2023-2024学年八年级上学期数学 12.2 三角形全等的判定 期末复习(吉林地区专用)
试卷更新日期：2023-12-19 类型：复习试卷
一、选择题
-
1.
小明不慎将一块三角形的玻璃摔碎成如图所示的四块（即图中标有1、2、3、4的四块），你认为将其中的哪一些块带去，就能配一块与原来一样大小的三角形？应该带（ ）
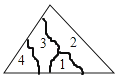A、第1块 B、第2块 C、第3块 D、第4块2. 如图，∠A=∠D，∠1=∠2，要使△ABC≌△DEF，还应给出的条件是（ ）
A、∠E=∠B B、ED=BC C、AB=EF D、AF=CD3. 如图，在由4个相同的小正方形拼成的网格中，∠2-∠1=（ ）
A、60° B、75° C、90° D、105°4. 如图，OB平分∠AOC，D，E，F分别是射线OA，射线OB，射线OC上的点，D，E，F与0点都不重合，连接ED， EF．若添加下列条件中的某一个，使△DOE≌△FOE．下列条件不一定成立的是（ ）
A、DE=FE． B、OD=OF． C、∠OED=∠OEF． D、∠ODE=∠OF．5. 如图，将一边长为a的正方形（最中间的小正方形）与四块边长为B的正方形（其中b>a）拼接在一起，则四边形ABCD的面积为（ ）
A、a2+2ab． B、a2+b2 ． C、（b+a）2 ． D、（b-a）2+b2 ．6. 如图，已知∠AOB．根据下列作图回答问题：①作射线O'A'； ②以O为圆心，以任意长为半径画弧，分别交OA、OB于点C、D；③以O'为圆心，以OC长为半径画弧，交O'A'于点C' ；④以点C为圆心，CD长为半径画弧，与第③步中所画的弧相交于点D' ；④过点D'画射线O'B'．则∠A'O'B'=∠AOB．这种作法正确的理由是（ ）
A、由SSS可得△O'C'D'≌△OCD，进而可证∠A'O'B'=∠AOB B、由SAS可得△O'C'D'≌△OCD，进而可证∠A'O'B'=∠AOB． C、由ASA可得△O'C'D'≌△OCD，进而可证∠A'O'B'=∠AOB． D、由“等边对等角”可得∠A'O'B'=∠AOB．7. 如图，已知∠1＝∠2，下列添加的条件不能使△ADC≌△CBA的是（ ）
A、AB∥DC B、AB＝CD C、AD＝BC D、∠B＝∠D8.如图所示，已知∠A＝∠D，∠1＝∠2，那么要得到△ABC≌△DEF，还应给出的条件是（ ）
A、∠E＝∠B B、ED＝BC C、AB＝EF D、AF＝CD二、填空题
-
9. 如图，在Rt△ABC和Rt△EDF中，BC=DF，在不添加任何辅助线的情况下，小明想利用HL的方法判定Rt△ABC和Rt△EDF全等，则还要添加的一个条件是
10. 如图，在四边形 ABCD中，AD∥BC，EF 过BD的中点O，分别交AD和BC于点E、F，若 OE = 2cm，则 OF =cm.
11. 如图，把两根钢条的中点连在一起。可以做成一个测量工件内槽的工具（卡钳）．在图中，若测量得A'B'=20cm．则工件内槽宽AB=cm
12. 用同种材料制成的金属框架如图所示，已知 ， ， ， 其中的周长为24cm， ， 则制成整个金属框架所需这种材料的长度为cm．
13. 如图，点E、C、F、B在一条直线上，EC＝BF， ， 当添加条件时，可由“角边角”判定△ABC≌△DEF．
14. 如图，AC与BD交于点O，连接AB、CD，∠A＝∠C，OB=OD，若AC＝10cm，则OA=cm．
三、解答题
-
15. 如图，∠A＝∠D ， ∠ACB＝∠DBC ． 求证：△ABC≌△DCB ．
16. 如图，点E在边AC上，CE =CB．∠A=∠D．∠DEC =∠ACB．求证：AB= CD．
17. 如图，E是AC上一点， ， 求证：
18. 如图，已知 ， ， 求证：.
19. 如图，在四边形ABCD中，AB=AD，∠B=∠D=90°，求证：BC=CD．
20. 如图，在△ABC中，CB⊥AB、∠BAC=45°，F是AB延长线上一点，点E在BC上，且AE=CF．求证：Rt△ABE≌Rt△CBF．
21. 如图，在△ABC和△ADE中，AB=AC，AD=AE，∠BAC=∠DAE，点C在DE上．
(1)、求证：∠BDA=∠E．(2)、若∠BDA=35°，则∠BDE=°22. 如图，在△ABC中，AB=AC，AD为△ABC的角平分线．以点A为圆心，AD长为半径面弧，与AB、AC分别交于点E、F，连接DE、DF．
(1)、求证：△ADE≌△ADF ；(2)、若∠BAC=80°．求∠BDE的度数．
