(人教版)2023-2024学年八年级上学期数学 12.1 全等三角形 期末复习(吉林地区专用)
试卷更新日期:2023-12-19 类型:复习试卷
一、选择题
-
1. 下列各组的两个图形属于全等图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 如图。△ABC≌△DEC.若∠DCB=85°,∠BCE=40°,则∠ACE的度数为( )
2. 如图。△ABC≌△DEC.若∠DCB=85°,∠BCE=40°,则∠ACE的度数为( ) A、5° B、10° C、15° D、20°3.
A、5° B、10° C、15° D、20°3.如图所示,△ABD≌△CDB,下面四个结论中,不正确的是( )
 A、△ABD和△CDB的面积相等 B、△ABD和△CDB的周长相等 C、∠A+∠ABD=∠C+∠CBD D、AD∥BC,且AD=BC4. 如图, ,点 在边 上,则下列结论中一定成立的是( )
A、△ABD和△CDB的面积相等 B、△ABD和△CDB的周长相等 C、∠A+∠ABD=∠C+∠CBD D、AD∥BC,且AD=BC4. 如图, ,点 在边 上,则下列结论中一定成立的是( ) A、 B、 C、 D、5. 如图,若△ABC≌△DEF , 且BE=5,CF=2,则BF的长为( )
A、 B、 C、 D、5. 如图,若△ABC≌△DEF , 且BE=5,CF=2,则BF的长为( ) A、2 B、3 C、1.5 D、56. 如图,△ABE≌△ACD,AB=AC,BE=CD,∠B=50°,∠AEC=120°,则∠DAC的度数等于( )
A、2 B、3 C、1.5 D、56. 如图,△ABE≌△ACD,AB=AC,BE=CD,∠B=50°,∠AEC=120°,则∠DAC的度数等于( )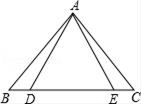 A、120° B、70° C、60° D、50°7. 如图,△ABC≌△EDF,∠FED=70°,则∠A的度数是( )
A、120° B、70° C、60° D、50°7. 如图,△ABC≌△EDF,∠FED=70°,则∠A的度数是( ) A、50° B、70° C、90° D、20°8.
A、50° B、70° C、90° D、20°8.如图,△ABC≌△DCB,若∠A=80°,∠ACB=40°,则∠BCD等于( )
 A、80° B、60° C、40° D、20°
A、80° B、60° C、40° D、20°二、填空题
-
9. 两个全等的直角三角形重叠在一起,将其中的一个三角形沿着点B到C的方向平移到△DEF的位置,AB=4,DO=1,平移距离为2,则阴影部分面积为
 10. 如图,在△ACB中,∠ACB=90°,AC=BC,点C的坐标为( -2,0),点A的坐标为(-6,3),则B点的坐标是
10. 如图,在△ACB中,∠ACB=90°,AC=BC,点C的坐标为( -2,0),点A的坐标为(-6,3),则B点的坐标是 11. 如图,已知AD=DE,AB=BE,若∠A=75°,则∠CED =度.
11. 如图,已知AD=DE,AB=BE,若∠A=75°,则∠CED =度. 12. 如图,四边形ABCD的对角线AC,BD相交于点O, , 下列结论:①;②;③;④.其中正确结论的序号是.
12. 如图,四边形ABCD的对角线AC,BD相交于点O, , 下列结论:①;②;③;④.其中正确结论的序号是. 13. 如图,已知△ABC≌△DBE,AB=5,BE=12,则CD的长为
13. 如图,已知△ABC≌△DBE,AB=5,BE=12,则CD的长为 14. 如图,△ABO≌△DCO,点B、D、A、C在同一直线上,若AD=1,BC=9,则BD=
14. 如图,△ABO≌△DCO,点B、D、A、C在同一直线上,若AD=1,BC=9,则BD=
三、解答题
-
15. 如图,在△ABC中,过点A作AE⊥BC,垂足为E,延长EA至点D,使AD=AC.在边AC上取一点F.连接DF.若∠DAF=110°,∠BAE=40°,∠D=∠C,求证:AF=AB.
 16. 如图,点在一条直线上,于 , 于 . 求证: .
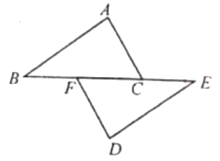
16. 如图,点在一条直线上,于 , 于 . 求证: . 17. 如图,点B、F、C,E在同一直线上,BF=CE,AB∥ED,AC∥FD.
17. 如图,点B、F、C,E在同一直线上,BF=CE,AB∥ED,AC∥FD.求证:AB=DE.
 18. 如图,△EFG≌△NMH,E,H,G,N在同一条直线上,EF和NM,FG和MH是对应边,若EH=1.1cm,NH=3.3cm.求线段HG的长.
18. 如图,△EFG≌△NMH,E,H,G,N在同一条直线上,EF和NM,FG和MH是对应边,若EH=1.1cm,NH=3.3cm.求线段HG的长. 19. 如图,ΔABD≌ΔEBC , AB=3cm , BC=5cm.求DE的长
19. 如图,ΔABD≌ΔEBC , AB=3cm , BC=5cm.求DE的长 20. 如图,已知 于点D, 于点E, , ,AB=8,AD=4,G为 延长线上一点,求 的度数和CE的长.
20. 如图,已知 于点D, 于点E, , ,AB=8,AD=4,G为 延长线上一点,求 的度数和CE的长. 21. 如图,已知△ACF≌△DBE,且点A,B,C,D在同一条直线上,∠A=50°,∠F=40°.
21. 如图,已知△ACF≌△DBE,且点A,B,C,D在同一条直线上,∠A=50°,∠F=40°.(1)求△DBE各内角的度数;
(2)若AD=16,BC=10,求AB的长.
 22. 如图,△ABC中,AD是BC边上的中线,E,F为直线AD上的点,连接BE,CF,且BE∥CF.
22. 如图,△ABC中,AD是BC边上的中线,E,F为直线AD上的点,连接BE,CF,且BE∥CF. (1)、求证:△BDE≌△CDF; .(2)、若AE=13,AF=7,求DE的长.23. 如图①,在△ABC中,∠ACB=90°,AC=BC,点P是线段AB上的一点,过点A作AE⊥CP,交CP的延长线于点E,过点B作BF⊥CP于点F.
(1)、求证:△BDE≌△CDF; .(2)、若AE=13,AF=7,求DE的长.23. 如图①,在△ABC中,∠ACB=90°,AC=BC,点P是线段AB上的一点,过点A作AE⊥CP,交CP的延长线于点E,过点B作BF⊥CP于点F. (1)、若BF=8,AE=3,则EF=(2)、在图①中,线段AE、BF、EF有怎样的数量关系?请说明理由;(3)、如图②,在△ABC中,∠ACB=90°,AC=BC,点P是△ABC内部的一点,且BP⊥CP,连接AP,若CP=5,求△ACP的面积.24. 如图,△ABC的两条高AD与BE交于点O,AD=BD,AC=6.
(1)、若BF=8,AE=3,则EF=(2)、在图①中,线段AE、BF、EF有怎样的数量关系?请说明理由;(3)、如图②,在△ABC中,∠ACB=90°,AC=BC,点P是△ABC内部的一点,且BP⊥CP,连接AP,若CP=5,求△ACP的面积.24. 如图,△ABC的两条高AD与BE交于点O,AD=BD,AC=6. (1)、求证:OB=AC;(2)、若∠ABO=25°,则∠EOD=°,∠ACB=°(3)、点F是射线BC上一点,且CF=AO,动点P从点O出发,沿线段OB以每秒1个单位长度的速度向终点B运动,同时动点Q从点A出发,沿射线AC以每秒4个单位长度的速度运动,当点P到达点B时,P,Q两点同时停止运动,设运动时间为t秒,当△AOP与△FCQ全等时,直接写出t的值.
(1)、求证:OB=AC;(2)、若∠ABO=25°,则∠EOD=°,∠ACB=°(3)、点F是射线BC上一点,且CF=AO,动点P从点O出发,沿线段OB以每秒1个单位长度的速度向终点B运动,同时动点Q从点A出发,沿射线AC以每秒4个单位长度的速度运动,当点P到达点B时,P,Q两点同时停止运动,设运动时间为t秒,当△AOP与△FCQ全等时,直接写出t的值.