2023~2024学年沪科版九年级上册期末数学质量评估卷【一】
试卷更新日期:2023-12-19 类型:期末考试
一、选择题(每题4分,共40分)
-
1. 下列图形中,既是轴对称图形,又是中心对称图形的是( )A、
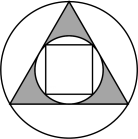 B、
B、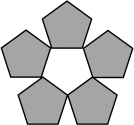 C、
C、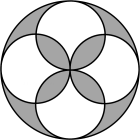 D、
D、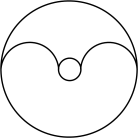 2. 中,D、E分别是边、上的点,下列各式中,能判断的是( )A、 B、 C、 D、3. 如图,在扇形中,D为弧上的点,连接并延长与的延长线交于点C,若 , , 则的度数为( )
2. 中,D、E分别是边、上的点,下列各式中,能判断的是( )A、 B、 C、 D、3. 如图,在扇形中,D为弧上的点,连接并延长与的延长线交于点C,若 , , 则的度数为( ) A、 B、 C、 D、4. 点都在反比例函数的图像上,且 , 则的大小关系是( )A、 B、 C、 D、5. 如图,在的正方形网格中,点A , B , C都在格点上,则的值为( )
A、 B、 C、 D、4. 点都在反比例函数的图像上,且 , 则的大小关系是( )A、 B、 C、 D、5. 如图,在的正方形网格中,点A , B , C都在格点上,则的值为( ) A、 B、 C、1 D、6. 在一次足球比赛中,某队守门员开出的球门球,经过第一次飞行后的落地点为 , 第二次从落地点反弹后继续向前飞行,落地点为 , 如图,已知第一次飞行经过秒时球距离地面的高度米适用公式 , 足球第二次飞行路线满足抛物线,且第二次飞行的最大高度和从反弹到落地所用时间均为第一次的一半,则足球第二次飞行所满足的函数表达式为( )
A、 B、 C、1 D、6. 在一次足球比赛中,某队守门员开出的球门球,经过第一次飞行后的落地点为 , 第二次从落地点反弹后继续向前飞行,落地点为 , 如图,已知第一次飞行经过秒时球距离地面的高度米适用公式 , 足球第二次飞行路线满足抛物线,且第二次飞行的最大高度和从反弹到落地所用时间均为第一次的一半,则足球第二次飞行所满足的函数表达式为( )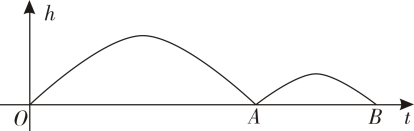 A、 B、
A、 B、
C、 D、7. 已知二次函数 , 若关于的方程的实数根为 , , 且 , 则下列不等式正确的是( )A、 , B、 C、 D、8. 如图,直线轴于点 , 且与反比例函数及的图象分别交于点 , , 连接 , , 已知的值为 , 则的面积为( ) A、 B、 C、 D、9. 如图,若 , , 与交于点 , 且 , , 则等于( )
A、 B、 C、 D、9. 如图,若 , , 与交于点 , 且 , , 则等于( )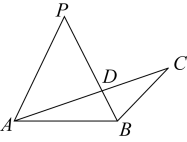 A、3 B、6 C、7 D、1210. 如图,在平面直角坐标系中,与轴交于A,B两点(在的左侧),与轴交于点 , 点是上方抛物线上一点,连结交于点 , 连结AC,CP,记的面积为 , 的面积为 , 则的最小值为( )
A、3 B、6 C、7 D、1210. 如图,在平面直角坐标系中,与轴交于A,B两点(在的左侧),与轴交于点 , 点是上方抛物线上一点,连结交于点 , 连结AC,CP,记的面积为 , 的面积为 , 则的最小值为( ) A、 B、 C、 D、1
A、 B、 C、 D、1二、填空题(每题5分,共20分)
-
11. 如图,斜坡的坡度 , 现需要在不改变坡高的情况下将坡度变缓,调整后的斜坡的坡度 , 已知斜坡米,那么斜坡米.
 12. 已知二次函数的图象与轴交于两点.若 , 则 .13. 如图,是⊙O的直径,点 , 在⊙O上, , 则 .
12. 已知二次函数的图象与轴交于两点.若 , 则 .13. 如图,是⊙O的直径,点 , 在⊙O上, , 则 . 14. 如图,在四边形中, , , , , , 分别为 , 上的点.连结 , , .
14. 如图,在四边形中, , , , , , 分别为 , 上的点.连结 , , . (1)、当点与点重合时, .(2)、若点不与点 , 重合,则 .
(1)、当点与点重合时, .(2)、若点不与点 , 重合,则 .三、计算题(共8分)
-
15. 计算;.
四、作图题(共2题,共16分)
-
16. 如图,在等腰直角△ABC中,∠ACB=90°,AC=BC=;
 (1)、作⊙O,使它过点A、B、C(要求尺规作图保留作图痕迹);(2)、在(1)所作的圆中,求圆心角∠BOC的度数和该圆的半径17. 在如图的方格纸中,的顶点坐标分别为 , , , 与是关于点P为位似中心的位似图形.
(1)、作⊙O,使它过点A、B、C(要求尺规作图保留作图痕迹);(2)、在(1)所作的圆中,求圆心角∠BOC的度数和该圆的半径17. 在如图的方格纸中,的顶点坐标分别为 , , , 与是关于点P为位似中心的位似图形.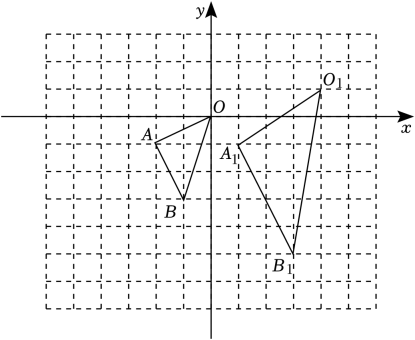
( 1 )在图中标出位似中心P的位置并直接写出点P的坐标为 .
( 2 )以原点O为位似中心,在位似中心的同侧画出的一个位似 , 使它与的位似比为2:1;
( 3 )的内部一点M的坐标为 , 直接写出点M在中的对应点的坐标为 .
五、解答题(共10分)
-
18. 如图所示是永州八景之一的愚溪桥,桥身横跨愚溪,面临潇水,桥下冬暖夏凉,常有渔船停泊桥下避晒纳凉.已知主桥拱为抛物线型,在正常水位下测得主拱宽24m,最高点离水面8m,以水平线AB为x轴,24m的中点为原点建立坐标系.

 (1)、求此桥拱线所在抛物线的解析式;(2)、桥边有一浮在水面部分高3.5m,最宽处m的河鱼餐船,试探索此船能否开到桥下?说明理由.
(1)、求此桥拱线所在抛物线的解析式;(2)、桥边有一浮在水面部分高3.5m,最宽处m的河鱼餐船,试探索此船能否开到桥下?说明理由.六、综合题(共5题,共56分)
-
19. 图1,图2分别是某超市购物车的实物图与示意图,小江获得了如下信息: , , , , , , , .请根据以上信息,解决下列问题.(结果精确到 , 参考数据: , , )
 (1)、求点D到所在直线的距离.(2)、求的长度.20. 如图,一次函数的图象与反比例函数的图象相交于点 , 两点.
(1)、求点D到所在直线的距离.(2)、求的长度.20. 如图,一次函数的图象与反比例函数的图象相交于点 , 两点. (1)、求反比例函数的解析式与点的坐标;(2)、连接、 , 求的面积;(3)、点是反比例函数图象上的一点,当时,求点的坐标.21. 如图所示,已知是的直径,过的中点 , 且 .
(1)、求反比例函数的解析式与点的坐标;(2)、连接、 , 求的面积;(3)、点是反比例函数图象上的一点,当时,求点的坐标.21. 如图所示,已知是的直径,过的中点 , 且 .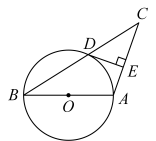 (1)、求证:是的切线;(2)、若 , cm,求的半径.22. 如图,在中, , 点分别在边上,满足 . 点是延长线上一点,且 .
(1)、求证:是的切线;(2)、若 , cm,求的半径.22. 如图,在中, , 点分别在边上,满足 . 点是延长线上一点,且 .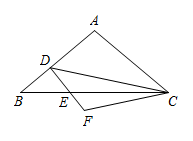 (1)、当点D是的中点时,求的值;(2)、如果 , 求的值;(3)、如果是等腰三角形,求的长.23. 已知抛物线(是常数)与x轴交于A,B两点,A在B的左侧.(1)、若抛物线的对称轴为直线 , 求抛物线的解析式;(2)、在(1)的条件下, , 是抛物线上的两点,点P是线段CD下方抛物线上的一动点,连接PC,PD,求的面积最大值;(3)、已知代数式 , 记抛物线位于轴下方的图象为 , 抛物线位于x轴上方的图象为 , 将沿轴翻折得图象 , 与组合成的新图象记为 , 当直线与图象T有两个交点时,结合图象求M的取值范围.
(1)、当点D是的中点时,求的值;(2)、如果 , 求的值;(3)、如果是等腰三角形,求的长.23. 已知抛物线(是常数)与x轴交于A,B两点,A在B的左侧.(1)、若抛物线的对称轴为直线 , 求抛物线的解析式;(2)、在(1)的条件下, , 是抛物线上的两点,点P是线段CD下方抛物线上的一动点,连接PC,PD,求的面积最大值;(3)、已知代数式 , 记抛物线位于轴下方的图象为 , 抛物线位于x轴上方的图象为 , 将沿轴翻折得图象 , 与组合成的新图象记为 , 当直线与图象T有两个交点时,结合图象求M的取值范围.
-
-