（人教版）2023-2024学年八年级上学期数学 11.3 多边形及其内角和期末复习(吉林地区专用)

试卷更新日期：2023-12-19 类型：复习试卷

进入出卷网下载

一、选择题

1. 若一个多边形的内角和等于1080°，则这个多边形的边数是 ( )

A、9 B、8 C、7 D、6

查看试题解析
2. 如图，将一个五边形ABCDE沿虚线裁去一个角后得到的多边形ABCDGF的内角和为（）

A、180° B、360° C、540° D、720°

查看试题解析
3. 某科技小组制作了一个机器人，它能根据指令要求进行行走和旋转，某一指令规定：机器人先向前行走2米，然后左转45°，若机器人反复执行这一指令，则从出发到第一次回到原处，机器人共走了（　　）

A、14米 B、15米 C、16米 D、17米

查看试题解析
4. 如图，将透明直尺叠放在正五边形徽章ABCDE上，若直尺的下沿MN⊥DE于点O，且经过点B，上沿PQ经过点E，则∠ABM的度数为（）

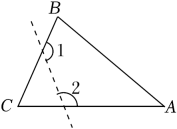
A、152° B、126° C、120° D、108°

查看试题解析
5. 从一个多边形的任何一个顶点出发都只有2条对角线，则它的边数是（）条.

A、3 B、4 C、5 D、6

查看试题解析
6. 下列说法中正确的是（　　）

A、两条对角线垂直的四边形的菱形 B、对角线垂直且相等的四边形是正方形 C、两条对角线相等的四边形是矩形 D、两条对角线相等的平行四边形是矩形

查看试题解析
7. 如图，直线 $l_{1} ∥ l_{2}$ ，正五边形ABCDE的顶点A ， B分别落在 $l_{1}$ ， $l_{2}$ 上.若 $∠ 1 = 25 °$ ，则∠2的度数为（）

A、60° B、61° C、62° D、65°

查看试题解析
8. 从 $n$ 边形的一个顶点引出的对角线把它最多划分为 $2023$ 个三角形，则 $n$ 的值为（）

A、 $2022$ B、 $2023$ C、 $2024$ D、 $2025$

查看试题解析

二、填空题

9. 十三边形的外角和为度．

查看试题解析
10. 若一个多边形的每一个外角都等于40°，则这个多边形是边形．

查看试题解析
11. 如图，在△ABC中，∠C＝70°，则∠1+∠2＝．

查看试题解析
12. 一个正方形、一个正三角形和一个正五边形如图摆放，若∠3＝34°，则∠1+∠2＝°．

查看试题解析
13. 如图，小陈从 $O$ 点出发，前进 $5$ 米后向右转 $20 °$ ，再前进 $5$ 米后又向右转 $20 °$ ， $\dots$ ，这样一直走下去，他第一次回到出发点 $O$ 时一共走了米．

查看试题解析
14. 若正n边形一个外角的度数为 $10 °$ ，则n的值为．

查看试题解析

三、解答题

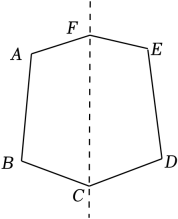
15. 已知一个多边形的内角和的 $\frac{1}{3}$ 等于它的外角和，求这个多边形的边数．

查看试题解析
16. 如图，六边形ABCDEF是轴对称图形，CF所在的直线是它的对称轴，若∠AFC+∠BCF=150°，求∠D+∠E的度数．

查看试题解析
17. 已知在一个十边形中，其中九个内角的和是 $1320 °$ ，求这个十边形另一个内角的度数．

查看试题解析
18. 已知正n边形的每个内角与其外角的差为90°，求这个多边形的每个内角度数与边数n．

查看试题解析
19. 如图所示，在四边形ABCD中，∠A＝80°，∠C=75°，∠ADE为四边形ABCD的一个外角，且∠ADE＝125°，试求出∠B的度数.

查看试题解析
20.
如图，求：∠A+∠B+∠C+∠D+∠E+∠F的度数．

查看试题解析
21. 阅读下列内容，并答题：
我们知道计算n边形的对角线条数公式为 $\frac{n (n - 3)}{2}$ ，如果有一个n边形的对角线一共有20条，则可以得到方程 $\frac{n (n - 3)}{2}$ =20，去分母得n（n﹣3）=40；∵n为大于等于3的整数，且n比n﹣3的值大3，∴满足积为40且相差3的因数只有8和5，符合方程n（n﹣3）=40的整数n=8，即多边形是八边形．根据以上内容，问：
（1）若有一个多边形的对角线一共有14条，求这个多边形的边数；
（2）A同学说：“我求得一个多边形的对角线一共有30条．”你认为A同学说地正确吗？为什么？

查看试题解析
22.
探索归纳：

(1)、如图1，已知△ABC为直角三角形，∠C=90°，若沿图中虚线剪去∠C，则∠1+∠2等于（）

A、90° B、135° C、270° D、315°

(2)、如图2，已知△ABC中，∠A=40°，剪去∠A后成四边形，则∠1+∠2=

(3)、如图2，根据（1）与（2）的求解过程，请你归纳猜想∠1+∠2与∠A的关系是

(4)、如图3，若没有剪掉，而是把它折成如图3形状，试探究∠1+∠2与∠A的关系并说明理由．

查看试题解析
23.
（1）已知：如图1，P为△ADC内一点，DP、CP分别平分DP、CP分别平公∠ADC和∠ACD，如果∠A=60°，那么∠P的度数；如果∠A=90°，那么∠P的度数；如果∠A=x°，则∠P的度数；（答案直接填在题中横线上）
（2）如图2，P为四边形ABCD内一点，DP、CP分别平分∠ADC和∠BCD，试探究∠P与∠A+∠B的数量关系，并写出你的探索过程；
（3）如图3，P为五边形ABCDE内一点，DP、CP分别平分DP、CP分别平公∠ADC和∠ACD，请直接写出∠P与∠A+∠B+∠E的数量关系
（4）如图4，P为六边形ABCDEF内一点，DP、CP分别平分DP、CP分别平公∠ADC和∠ACD，请直接写出∠P与∠A+∠B+∠E+∠F的数量关系
（5）若P为n边形A₁A₂A₃…A_n内一点，PA₁平分∠A_nA₁A₂ ， PA₂平分∠A₁A₂A₃ ，请直接写出∠P与∠A₃+A₄+A₅+…∠A_n的数量关系：

查看试题解析
24.
多边形的内角和随着边数的变化而变化．设多边形的边数为n，内角和为N，则变量N与n之间的关系可以表示为N=（n﹣2）•180°．
例如：如图四边形ABCD的内角和：
N=∠A+∠B+∠C+∠D=（4﹣2）×180°=360°

(1)、利用这个关系式计算五边形的内角和

(2)、当一个多边形的内角和N=720°时，求其边数n．

查看试题解析

（人教版）2023-2024学年八年级上学期数学 11.3 多边形及其内角和 期末复习(吉林地区专用)

一、选择题

二、填空题

三、解答题

（人教版）2023-2024学年八年级上学期数学 11.3 多边形及其内角和期末复习(吉林地区专用)