（人教版）2023-2024学年七年级上学期数学 4.1 几何图形 期末复习(吉林地区专用)
试卷更新日期：2023-12-19 类型：复习试卷
一、选择题
-
1. 如图是一个多面体展开图，每个面都标注了数字。若多面体的底面是⑤，则多面体的上面是（ ）
A、面① B、面② C、面③ D、面⑥2.一个几何体的展开图如图所示，这个几何体是（ ）
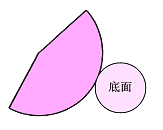A、圆锥 B、圆柱 C、四棱柱 D、四棱锥3. 用平面截一个正方体，可能截出的边数最多的多边形是（ ）A、七边形 B、六边形 C、五边形 D、四边形4. 下列说法中，正确的个数是（ ）①柱体的两个底面一样大；②圆柱、圆锥的底面都是圆；③棱柱的底面是四边形；
④长方体一定是柱体；⑤棱柱的侧面一定是长方形．
A、2个 B、3个 C、4个 D、5个5. 下面给出的图形中，绕虚线旋转一周能形成圆锥的是（ ）A、
B、
C、
D、
6. 一个骰子相对两面的点数之和为7，它的展开图如图所示，下列判断正确的是（ ）
A、A代表
B、B代表
C、B代表
D、C代表
7. 如图，下面的平面图形绕轴旋转一周，可以得到圆柱体的是（ ）A、
B、
C、
D、
8. 我们生活在三维的世界中，随时随地看到的和接触到的物体都是立体的．下面这个物体可以抽象成哪种几何体（ ）
A、棱锥 B、棱柱 C、圆锥 D、圆柱二、填空题
-
9. 如图，在有序号的小正方形中选出一个，它与图中五个有阴影的小正方形组合后，能构成正方体的表面展开图的是 ．
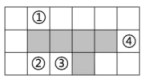10. 一个正方体的平面展开图如图所示。若将展开图折叠成正方体后，相对面上所标的两个数互为相反数，则的值为 ．
11. 把如图所示的图形折成一个正方体盒子，折好后与“欢”相对的字是 ．
12. 水平放置的正方体的六个面分别用“前面、后面、上面、下面、左面、右面”表示，如图是正方体的平面展开图，若图中的“锦”表示正方体的右面，则“”表示正方体的左面
13. 若要使得图中平面展开图折叠成正方体后，相对面上的两个数之和相等，则的值为 ．
14. 如图是正方体的展开图，则原正方体相对两个面上的数字之和的最小值的是 ．
三、解答题
-
15. 用数学的眼光观察问题，你会发现很多图形都能看成是动静结合，舒展自如的．下面所给的三排图形(如图)，都存在着某种联系．用线将存在联系的图形连接起来．
16. 如图，在无阴影的方格中选出两个画出阴影，使它们与图中4个有阴影的正方形一起可以构成一个正方体的表面展开图．（在图1和图2中任选一个进行解答，只填出一种答案即可）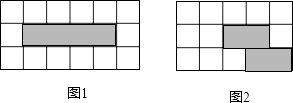
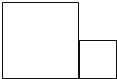
17.如图，由2个正方形拼成的图形中，如何把它们分成形状、大小完全相同的四部分？请你在图中把这四部分表示出来．
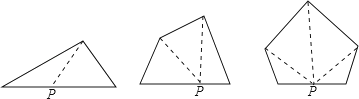
18.如图，从一个多边形的某一条边上的一点（不与端点重合）出发，分别连接这个点与其他所有顶点，可以把这个多边形分割成若干个三角形，由三角形、四边形、五边形为例，你能总结出什么规律？n边形呢？
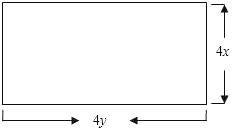
19.人人争当小小设计师．一个工程队为建设一项重点工程，要在一块长方形荒地上建造几套简易住房，每一套简易住房的平面是由长4y、宽4x构成，要求建成：两室、一厅、一厨、一卫．其中客厅面积为6xy；两个卧室的面积和为8xy；厨房面积为xy；卫生间面积为xy．请你根据所学知识，在所给图中设计其中一套住房的平面结构示意图．
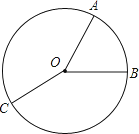
20.如图是半径为2的圆．
（1）在其中画两个不重叠的扇形AOB和扇形BOC，使扇形AOB的圆心角为120°，扇形BOC的圆心角为90°；
（2）求第三个扇形AOC的面积．
21.如图①、②、③、④四个图形都是平面图形，观察图②和表中对应数值，探究计数的方法并解答下面的问题．
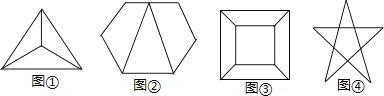
（1）数一数每个图各有多少顶点、多少条边、这些边围成多少区域，将结果填入下表：
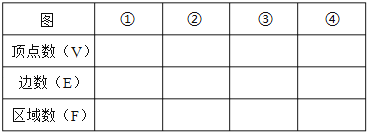
（2）根据表中的数值，写出平面图的顶点数、边数、区域数之间的关系；
（3）如果一个平面图形有20个顶点和11个区域，求这个平面图形的边数．
22. 将一个半径为2cm的圆分成3个扇形，其圆心角的比1：2：3，求：（1）各个扇形的圆心角的度数．
（2）其中最大一个扇形的面积．
23.如图，OA，OB，OC是圆的三条半径．
（1）若他们的圆心角度数比为1：2：3，求这三个扇形的圆心角的度数．
（2）在（1）的条件下，若圆的半径为2cm，求这三个扇形的面积．（保留π）
24.如图①，从大正方体上截去一个小正方体之后，可以得到图②的几何体．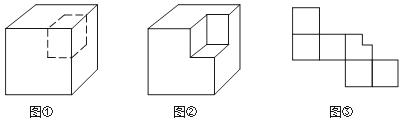
（1）设原大正方体的表面积为S，图②中几何体的表面积为S1 ， 那么S1与S的大小关系是
A．S1＞S B．S1=S C．S1＜S D．无法确定
（2）小明说：“设图①中大正方体各棱的长度之和为l，图②中几何体各棱的长度之和为l1 ， 那么l1比l正好多出大正方体3条棱的长度．”你认为这句话对吗？为什么？
（3）如果截去的小正方体的棱长为大正方体棱长的一半，那么图③是图②中几何体的表面展开图吗？如有错误，请予修正．