（人教版）2023-2024学年七年级上学期数学 1.5 有理数的乘方期末复习(吉林地区专用)

试卷更新日期：2023-12-19 类型：复习试卷

进入出卷网下载

一、选择题

1. 吉林油田立足自身油气开发生产实际，推进开源节流降本增效工程，坚决打赢提质增效攻坚战．今年第一季度生产原油1057000吨．数据1057000用科学记数法表示为（　　）

A、1.057×10⁵ B、10.57×10⁵ C、1.057×10⁶ D、0.1057×10⁷

查看试题解析
2. 数据8.641按四舍五人精确到0.01的结果是（）

A、8.6 B、9.0 C、8.65 D、8.64

查看试题解析
3. 一般地，数学上把 $\underset{n}{\underset{⏟}{a \cdot a . . . a}}$ 记作（）

A、n+a B、na C、n^a D、aⁿ

查看试题解析
4. -7×7×7×7×7×7可以表示为（）

A、（-7）⁶ B、-7⁶ C、（-7）×6 D、（-6）×7

查看试题解析
5. 长江是我国最长的河流，长度约为6300km，下列说法正确的是（）

A、这个数是准确数 B、这个数是近似数，精确到百位 C、这个数是近似数，精确到个位 D、这个数是近似数，精确到千位

查看试题解析
6. 近似数 $4.6 \times 1 0^{2}$ 精确到的位数是（）

A、十分位 B、个位 C、十位 D、百位

查看试题解析
7. 计算(-4)²的结果等于（）

A、8 B、-8 C、16 D、-16

查看试题解析
8. 我国与“一带一路”沿线国家货物贸易进出口总额达到13400亿美元，用科学记数法表示：13400应为（）

A、 $0.134 \times 1 0^{5}$ B、 $1.34 \times 1 0^{4}$ C、 $134 \times 1 0^{3}$ D、 $1.34 \times 1 0^{5}$

查看试题解析

二、填空题

9. 对于近似数0.183，精确到位．

查看试题解析
10. 用四舍五入法对3.444 5取近似数，即3.4445 （精确到百分位）≈

查看试题解析
11. 节约是一种美德，节约是一种智慧，据不完全统计，全国每年浪费食物总量折合粮食可养活约350000000人，数据350000000用科学记数法表示为

查看试题解析
12. 计算：（-1）²⁰²⁴-（-1）²⁰²³=

查看试题解析
13. 用四舍五入法，把155.628精确到个位的近似数是

查看试题解析
14. 亚洲陆地面积约为44000000平方千米，将44000000用科学记数法表示为．

查看试题解析

三、解答题

15. 老师设计了一个接力游戏，用合作的方式完成有理数运算，规则是：每人只能看到前一人给的式子，并进行一步计算，再将结果传递给下一人，最后完成计算过程如图所示：

(1)、计算错误的学生是；

(2)、请写出正确的计算过程．

查看试题解析
16. 已知a，b互为相反数，c，d互为倒数，x的绝对值为 $5$ ．

(1)、a+b = ， cd = ， x = .

(2)、求 ${(a + b + c d)}^{2024} + {(- c d)}^{2023} - x$ 的值．

查看试题解析
17. 若 $| x - 1 | + {(y + 2)}^{2} = 0$ ，求 $x - y$ 的值．

查看试题解析
18. 已知 $a$ 与 $b$ 互为相反数， $c$ 与 $d$ 互为倒数， $x$ 的平方等于4，试求 $4 x^{2} - (a + b + c d) x + (a + b)^{20222} + (- c d)^{2021}$ 的值．

查看试题解析
19. 小欢和小丽都十分喜欢唱歌．她们两人一起参加学校的文艺汇演．在汇演前，主持人让她们自己确定出场顺序，可她们俩争着先出场，最后主持人想出了一个主意，说：“给你们五张卡片，每张卡片上都有一些数．将化简后的数在数轴上表示出来，再用“ $<$ ”连接起来，（连接化简后的数）谁先按照要求做对，谁先出场”请你帮助她们解决这个问题．

查看试题解析
20. 阅读材料，求值：1+2+2²+2³+2⁴+…+2²⁰¹⁵ ．
解：设S=1+2+2²+2³+2⁴+…+2²⁰¹⁵ ，将等式两边同时乘以2得：
2S=2+2²+2³+2⁴+…+2²⁰¹⁵+2²⁰¹⁶
将下式减去上式得2S﹣S=2²⁰¹⁶﹣1
即S=1+2+2²+2³+2⁴+…+2²⁰¹⁵=2²⁰¹⁶﹣1
请你仿照此法计算：
（1）1+2+2²+2³+…+2¹⁰
（2）1+3+3²+3³+3⁴+…+3ⁿ（其中n为正整数）

查看试题解析
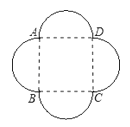
21. 2013年12月14日21时11分，嫦娥三号成功登陆月球．北京飞控中心通过无线电波控制，将“嫦娥三号”着陆器与巡视器成功分离的画面传回到大屏幕上．已知无线电波传播速度为3×10⁵km/s，无线电波到月球并返回地面用2.57s，求此时月球与地球之间的距离（精确到1000km）．

查看试题解析
22.
如图，某花坛由四个半圆和一个正方形组成，已知正方形的面积为16cm² ，求该花坛的周长．（π=3.1415，计算结果保留三个有效数字）

查看试题解析
23. 下表是我国的几个省（自治区）的年降水量以及纬度位置．
省（自治区）
广东省
湖北
河南
内蒙古
自治区
纬度位置
（北纬）
3度至25度
29度至33度
31度至36度
38度至53度
年降水量
1800毫米
1200毫米
900毫米
300毫米
（1）表中的数字都是近似数，其中四个年降水量都是精确到100毫米得到的，那么广东省的年降水量1800毫米这个近似数有几个有效数字．
（2）请选择合适的统计图，把这几个省的降水量尽可能的形象的表示出来．

查看试题解析
24. 如图在数轴上A点表示数a，B点表示数b，a、b满足|a+2|+（b-4）²＝0．

(1)、点A表示的数为；点B表示的数为；

(2)、若在原点O处放一挡板，一小球甲从点A处以1个单位/秒的速度向左运动；同时另一小球乙从点B处以3个单位/秒的速度也向左运动，在碰到挡板后（忽略球的大小，可看作一点）以原来的速度向相反的方向运动，设运动的时间为t（秒），
①当t＝1时，甲小球到原点的距离＝ ▲ ；乙小球到原点的距离＝ ▲ ；
当t＝2时，甲小球到原点的距离＝ ▲ ；乙小球到原点的距离＝ ▲ ；
②试探究：甲，乙两小球到原点的距离可能相等吗？若不能，请说明理由若能，请求出甲，乙两小球到原点的距离相等时t的值．
③若当甲和乙开始运动时，挡板也从原点以1个单位/秒的速度向右运动，直接写出甲，乙两小球到挡板的距离相等时t的值．

查看试题解析

（人教版）2023-2024学年七年级上学期数学 1.5 有理数的乘方 期末复习(吉林地区专用)

一、选择题

二、填空题

三、解答题

（人教版）2023-2024学年七年级上学期数学 1.5 有理数的乘方期末复习(吉林地区专用)