人教版数学六年级下册第3单元综合素质达标
试卷更新日期:2023-12-18 类型:单元试卷
一、填空。(每空1分,共17分)
-
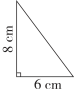
1. 750cm2=dm2 2.05dm3=LmL2. 给一个底面半径是10厘米,高是30厘米的圆柱形奶粉筒侧面贴满包装纸,至少需要平方厘米的包装纸。3. 如图,分别以直角三角形的两条直角边所在直线为轴旋转一周,所得到的立体图形的体积差是cm3。
 4. 一个圆锥的体积是4.5立方分米,高是4.5分米,那么它的底面积是平方分米。5. 把一根长2m的圆柱形木料沿横截面锯成三段,表面积增加了12.56dm2 , 这根圆柱形木料的体积是dm3。6. 把一个圆柱削成一个最大的圆锥,体积减少了120立方厘米,那么圆锥的体积是立方厘米。若圆锥的高是5厘米,它的底面积是平方厘米。7. 像长方体、正方体和圆柱这样的立体图形叫作柱体。柱体的体积都可以用底面积乘高来表示,即V=S底h。将图1所示圆柱沿底面半径(r)分成16等份,再按图2所示方式摆放拼成一个近似的长方体。转化后,长方体的体积等于圆柱的体积,长方体的底面积等于圆柱的底面积,长方体的高等于圆柱的高。
4. 一个圆锥的体积是4.5立方分米,高是4.5分米,那么它的底面积是平方分米。5. 把一根长2m的圆柱形木料沿横截面锯成三段,表面积增加了12.56dm2 , 这根圆柱形木料的体积是dm3。6. 把一个圆柱削成一个最大的圆锥,体积减少了120立方厘米,那么圆锥的体积是立方厘米。若圆锥的高是5厘米,它的底面积是平方厘米。7. 像长方体、正方体和圆柱这样的立体图形叫作柱体。柱体的体积都可以用底面积乘高来表示,即V=S底h。将图1所示圆柱沿底面半径(r)分成16等份,再按图2所示方式摆放拼成一个近似的长方体。转化后,长方体的体积等于圆柱的体积,长方体的底面积等于圆柱的底面积,长方体的高等于圆柱的高。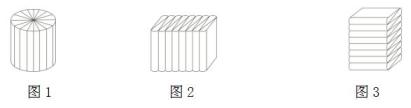 (1)、如果圆柱切分后按图3所示方式摆放,此时长方体的底面积= , 长方体的高= , V圆柱=V长方体=。(用字母r、h表示,保留π)(2)、把高是8cm的圆柱切分后按图2所示方式摆放,表面积增加了80cm2 , 这个圆柱的体积是cm3。8. 一个圆柱和一个圆锥的体积相等,底面半径也相等,圆柱的高是3.6dm,圆锥的高是dm。9. 一个圆柱,如果高增加1cm,那么它的侧面积就增加25.12cm2 , 如果这个圆柱的高是25cm,那么这个圆柱的体积是cm3。10. 一个圆锥和一个圆柱的体积相等,它们底面半径的比是3∶2,圆锥的高是16cm,圆柱的高是cm。11. 龙龙把一块棱长为8cm的正方体橡皮泥做成了组合在一起的等底等高的一个圆柱和一个圆锥(如下图),其中这个圆锥的体积是cm3。
(1)、如果圆柱切分后按图3所示方式摆放,此时长方体的底面积= , 长方体的高= , V圆柱=V长方体=。(用字母r、h表示,保留π)(2)、把高是8cm的圆柱切分后按图2所示方式摆放,表面积增加了80cm2 , 这个圆柱的体积是cm3。8. 一个圆柱和一个圆锥的体积相等,底面半径也相等,圆柱的高是3.6dm,圆锥的高是dm。9. 一个圆柱,如果高增加1cm,那么它的侧面积就增加25.12cm2 , 如果这个圆柱的高是25cm,那么这个圆柱的体积是cm3。10. 一个圆锥和一个圆柱的体积相等,它们底面半径的比是3∶2,圆锥的高是16cm,圆柱的高是cm。11. 龙龙把一块棱长为8cm的正方体橡皮泥做成了组合在一起的等底等高的一个圆柱和一个圆锥(如下图),其中这个圆锥的体积是cm3。
二、判断。(每小题1分,共5分)
-
12. 一个圆柱的底面周长和高相等,那么它的侧面沿高展开一定是正方形。 ( )13. 圆柱的体积一般比它的表面积大。
14. 底面积相等的两个圆柱,它们的体积也一定相等。 ( )15. 从圆锥的顶点向底面垂直切割,所得到的截面是一个等腰三角形。 ( )16. 圆柱的底面半径扩大到原来的2倍,高也扩大到原来的2倍,则圆柱的体积扩大到原来的4倍。 ( )三、选择。(将正确答案的字母填在括号里。每小题2分,共16分)
-
17. 圆柱的高和底面上任意一条半径所组成的角是( )。A、锐角 B、直角 C、钝角 D、平角18. 下面测量圆锥的高的方法正确的是( )。A、
 B、
B、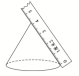 C、
C、 D、
D、 19. 一个长方体、一个圆柱和一个圆锥底面积相等,高也相等。下面说法正确的是( )。A、圆柱的体积比长方体的体积小一些 B、圆锥的体积是长方体体积的 C、圆柱的体积和圆锥的体积相等 D、圆锥的体积最大20. 典典、聪聪两人分别将一张长6.28cm,宽3.14cm的长方形纸以不同的方法围成一个圆柱(接头处不重叠),那么围成的两个圆柱的( )。A、高一定相等 B、侧面积一定相等 C、底面积一定相等 D、体积一定相等21. 选择材料,做一个圆柱形的容器,其中不能做成的是( )。
19. 一个长方体、一个圆柱和一个圆锥底面积相等,高也相等。下面说法正确的是( )。A、圆柱的体积比长方体的体积小一些 B、圆锥的体积是长方体体积的 C、圆柱的体积和圆锥的体积相等 D、圆锥的体积最大20. 典典、聪聪两人分别将一张长6.28cm,宽3.14cm的长方形纸以不同的方法围成一个圆柱(接头处不重叠),那么围成的两个圆柱的( )。A、高一定相等 B、侧面积一定相等 C、底面积一定相等 D、体积一定相等21. 选择材料,做一个圆柱形的容器,其中不能做成的是( )。
 A、甲和① B、甲和② C、乙和① D、乙和③22. 一个圆柱和一个圆锥的底面直径相等,圆锥的高是圆柱的3倍,圆锥的体积是12dm3 , 圆柱的体积是( )dm3。A、4 B、8 C、12 D、3623. 一个圆柱和一个圆锥,底面积的比是2∶3,它们的体积相等。圆柱和圆锥的高的最简整数比是( )。A、1∶2 B、5∶12 C、8∶5 D、2∶124. 如下图,要把下面三堆圆锥形沙子分别装在圆柱形的铁桶中(铁桶厚度忽略不计),下面是三名同学经过测量后得到的结论。
A、甲和① B、甲和② C、乙和① D、乙和③22. 一个圆柱和一个圆锥的底面直径相等,圆锥的高是圆柱的3倍,圆锥的体积是12dm3 , 圆柱的体积是( )dm3。A、4 B、8 C、12 D、3623. 一个圆柱和一个圆锥,底面积的比是2∶3,它们的体积相等。圆柱和圆锥的高的最简整数比是( )。A、1∶2 B、5∶12 C、8∶5 D、2∶124. 如下图,要把下面三堆圆锥形沙子分别装在圆柱形的铁桶中(铁桶厚度忽略不计),下面是三名同学经过测量后得到的结论。晶晶说:“第一堆和铁桶等底等高,能装下。”
明明说:“第二堆和铁桶等底,高是圆柱形铁桶的2倍,能装下。”
康康说:“第三堆和铁桶等高,底面半径是圆柱形铁桶的2倍,能装下”。
你认为( )的说法是正确的。
 A、三人都对 B、晶晶和明明 C、明明和康康 D、晶晶和康康
A、三人都对 B、晶晶和明明 C、明明和康康 D、晶晶和康康四、图形计算。(共21分)
-
25. 计算圆锥的体积。(单位:m)
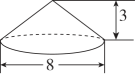 26. 求空心圆柱的表面积和体积。(单位:dm)
26. 求空心圆柱的表面积和体积。(单位:dm)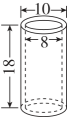 27. 从一个圆柱中挖去一个圆锥(如图所示),请计算剩余部分的体积。(单位:cm)
27. 从一个圆柱中挖去一个圆锥(如图所示),请计算剩余部分的体积。(单位:cm)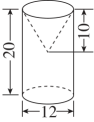
五、解决问题。(共41分)
-
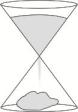
28. 每年的6月5日是世界环境日,它的设立表达了人类对美好环境的向往和追求。笑笑家为了节约用水,做了一个无盖的圆柱形铁皮水桶蓄水,高10分米,底面直径是高的 , 做这个水桶至少要用多少平方分米的铁皮?29. 一堆沙子呈圆锥形,底面周长是31.4米,高是1.5米,每立方米沙子约重1.8吨。(1)、这堆沙子的占地面积是多少平方米?(2)、这堆沙子大约有多少吨?30. 欢欢一家到餐馆吃饭,点完菜后服务员把一个沙漏摆到桌上,并且说“给您计个时,沙漏漏完前您点的菜都会上桌。”欢欢发现这是一个上下均为圆锥的沙漏(如图),两个圆锥的底面直径均是10厘米,高均是6厘米。上面的圆锥中装满沙子,如果每分钟漏掉10立方厘米的沙子,那么按服务员的承诺,欢欢一家点的菜全部上桌最多需要多少分钟?(得数保留整数)
 31. 一个圆柱的底面周长和高相等,如果高增加4cm,表面积就增加125.6cm2 , 原来这个圆柱的表面积是多少平方厘米?32. 一个圆柱形容器的内底面直径是20cm,容器中装有水。把一个铁球放入这个容器后,这个铁球完全没入水中,水面上升了3cm(水未溢出),这个铁球的体积是多少立方厘米?33. 为了测量一个空瓶子的容积,一个学习小组进行了如下实验。
31. 一个圆柱的底面周长和高相等,如果高增加4cm,表面积就增加125.6cm2 , 原来这个圆柱的表面积是多少平方厘米?32. 一个圆柱形容器的内底面直径是20cm,容器中装有水。把一个铁球放入这个容器后,这个铁球完全没入水中,水面上升了3cm(水未溢出),这个铁球的体积是多少立方厘米?33. 为了测量一个空瓶子的容积,一个学习小组进行了如下实验。①测量出整个瓶子的高度是23cm;
②测量出瓶子圆柱形部分的内直径是6cm;
③给瓶子里注入一些水,把瓶子正放时,测量出水的高度是5cm;
④把瓶子倒放时,无水部分是圆柱形,测量出它的高度是15cm。
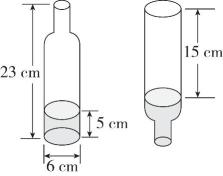 (1)、要求这个瓶子的容积,上面的记录中有用的信息是。(填序号)(2)、通过实验发现:瓶子的容积=+ , 运用了的数学思想。这一数学思想在我们小学阶段应用十分广泛,我们在学习时也运用了这一数学思想。(3)、请根据选出的信息,求出这个瓶子的容积。
(1)、要求这个瓶子的容积,上面的记录中有用的信息是。(填序号)(2)、通过实验发现:瓶子的容积=+ , 运用了的数学思想。这一数学思想在我们小学阶段应用十分广泛,我们在学习时也运用了这一数学思想。(3)、请根据选出的信息,求出这个瓶子的容积。