人教版(贵州地区)初中数学2023-2024学年九年级上学期期末模拟卷(三)
试卷更新日期:2023-12-18 类型:期末考试
一、选择题
-
1. 下列标志中,是中心对称图形但不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列事件中,属于必然事件的是( )A、小明买彩票中奖 B、任意抛掷一只纸杯,杯口朝下 C、任选三角形的两边,其差小于第三边 D、在一个没有红球的盒子里摸球,摸到了红球3. 下列方程中,不是一元二次方程的是( )A、2x2+7=0 B、2x2+2x+1=0 C、5x2+ +4=0 D、3x2+1=7x4. 关于x的一元二次方程的根的情况是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、不能确定5. 抛物线y=2x2与y=-2x2相同的性质是( )A、开口向下 B、对称轴是y轴 C、有最低点 D、对称轴是x轴6. 下列命题为真命题的是( ).A、三点确定一个圆 B、度数相等的弧相等 C、90°的圆周角所对的弦是直径 D、相等的圆心角所对的弧相等,所对的弦也相等7. 如图,在正方形网格中,将绕某一点旋转某一角度得到 , 则旋转中心是( )
2. 下列事件中,属于必然事件的是( )A、小明买彩票中奖 B、任意抛掷一只纸杯,杯口朝下 C、任选三角形的两边,其差小于第三边 D、在一个没有红球的盒子里摸球,摸到了红球3. 下列方程中,不是一元二次方程的是( )A、2x2+7=0 B、2x2+2x+1=0 C、5x2+ +4=0 D、3x2+1=7x4. 关于x的一元二次方程的根的情况是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、不能确定5. 抛物线y=2x2与y=-2x2相同的性质是( )A、开口向下 B、对称轴是y轴 C、有最低点 D、对称轴是x轴6. 下列命题为真命题的是( ).A、三点确定一个圆 B、度数相等的弧相等 C、90°的圆周角所对的弦是直径 D、相等的圆心角所对的弧相等,所对的弦也相等7. 如图,在正方形网格中,将绕某一点旋转某一角度得到 , 则旋转中心是( ) A、点A B、点B C、点C D、点D8. 如表是一组二次函数y=x2﹣x﹣3的自变量和函数值的关系,那么方程x2﹣x﹣3=0的一个近似根是( )
A、点A B、点B C、点C D、点D8. 如表是一组二次函数y=x2﹣x﹣3的自变量和函数值的关系,那么方程x2﹣x﹣3=0的一个近似根是( )x
1
2
3
4
y
﹣3
﹣1
3
9
A、1.2 B、2.3 C、3.4 D、4.59. 如图,延长圆内接四边形ABCD的边AB,DC,相交于点E,延长边AD,BC,相交于点F.若∠E=30°,∠F=50° ,则∠A的度数为( ). A、20° B、30° C、50° D、60°10. 在同一平面直角坐标系中,一次函数 和二次函数 的图象大致为( )A、
A、20° B、30° C、50° D、60°10. 在同一平面直角坐标系中,一次函数 和二次函数 的图象大致为( )A、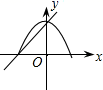 B、
B、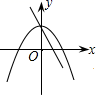 C、
C、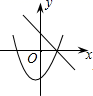 D、
D、
二、填空题
-
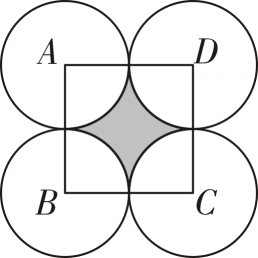
11. 方程的根是 .12. 点M(1,3)关于原点的对称点的坐标为13. 掷一枚质地均匀的硬币,前9次都是反面朝上,则掷第10次时反面朝上的概率是 .14. 若关于x的一元二次方程mx2+2x+m2-1=0的常数项为0,则m=15. 已知⊙O的半径为2cm , 则⊙O最长的弦为cm .16. 如果点在抛物线上,那么(“”、“=”或“”)17. 如图,正方形ABCD的边长是4,分别以点A , B , C , D为圆心,2为半径作圆,则图中阴影部分的面积是(结果保留).
三、计算题
-
18.(1)、解方程: .(2)、解不等式组: .
四、解答题
-
19. 若x1 , x2是一元二次方程2x2+4x-1=0的两个根,求下列式子的值.(1)、;(2)、 .20. 在 的方格中,△ABC的三个顶点都在格点上.
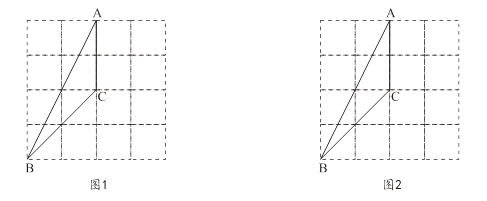 (1)、在图1中画出与△ABC成轴对称且与△ABC有公共边的格点三角形(画出一个即可);(2)、将图2中的△ABC绕着点C按顺时针方向旋转90°,画出经旋转后的三角形.21. 已知,如图,点E是正方形ABCD的边BC上一点,逆时针旋转后能够与重合.
(1)、在图1中画出与△ABC成轴对称且与△ABC有公共边的格点三角形(画出一个即可);(2)、将图2中的△ABC绕着点C按顺时针方向旋转90°,画出经旋转后的三角形.21. 已知,如图,点E是正方形ABCD的边BC上一点,逆时针旋转后能够与重合. (1)、旋转中心是 , 旋转角为度;(2)、请你判断的形状,并说明理由.22. 如图,两个可自由转动的转盘A,B分别被分成4等份、3等份,每份内标有数字,小王和小刘用这两个转盘做游戏,游戏规则如下:
(1)、旋转中心是 , 旋转角为度;(2)、请你判断的形状,并说明理由.22. 如图,两个可自由转动的转盘A,B分别被分成4等份、3等份,每份内标有数字,小王和小刘用这两个转盘做游戏,游戏规则如下: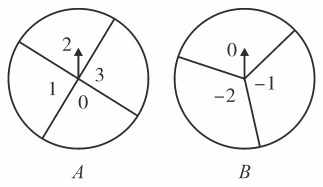
①分别转动转盘A,B;
②两个转盘停止转动后,将指针所指区域的数相加(如果指针恰好停在等分线上,那么重转一次,直到指针指向某一区域为止);
③如果和为0,那么小王获胜:否则,小刘获胜.
(1)、用列表法(或画树状图)求小王获胜的概率.(2)、你认为这个游戏对双方公平吗?请说明理由。23. 某玩具厂计划生产一种玩具熊猫,每日最高产量为40只,且每日产出的产品全部售出.已知生产x只玩具熊猫的成本为m(元),售价每只为n(元),且m、n与x的关系式分别为 , .(1)、当日产量为多少时,每日获得的利润为1750元?(2)、当日产量为多少时,可获得最大利润?最大利润是多少?24. 如图,在Rt△ABC中,∠ACB=90°,点O在边AC上,以点O为圆心,OC为半径的半圆与斜边AB相切于点D , 交OA于点E , 连结OB .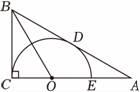 (1)、求证:BD=BC .(2)、已知OC=1,∠A=30°,求AB的长.25. 如图,在某场足球比赛中,球员甲从球门底部中心点O的正前方10 m处起脚射门,足球沿抛物线飞向球门中心线.当足球飞离地面高度为3 m时达到最高点,此时足球飞行的水平距离为6 m已知球门的横梁高为2.44 m.
(1)、求证:BD=BC .(2)、已知OC=1,∠A=30°,求AB的长.25. 如图,在某场足球比赛中,球员甲从球门底部中心点O的正前方10 m处起脚射门,足球沿抛物线飞向球门中心线.当足球飞离地面高度为3 m时达到最高点,此时足球飞行的水平距离为6 m已知球门的横梁高为2.44 m. (1)、建立如图所示直角坐标系。此次射门,足球能否射进球门(不计其他影响因素)?(2)、守门员站在距离球门2 m处,他跳起时手的最大摸高为2.52 m.问:他能阻止球员甲的此次射门吗?如果不能,他至少后退多少米才能阻止球员甲的此次射门?
(1)、建立如图所示直角坐标系。此次射门,足球能否射进球门(不计其他影响因素)?(2)、守门员站在距离球门2 m处,他跳起时手的最大摸高为2.52 m.问:他能阻止球员甲的此次射门吗?如果不能,他至少后退多少米才能阻止球员甲的此次射门?
-