人教版（贵州地区）初中数学2023-2024学年九年级上学期期末模拟卷（二）

试卷更新日期：2023-12-18 类型：期末考试

进入出卷网下载

一、选择题

1. 习近平总书记指出：发展新能源汽车是我国从汽车大国走向汽车强国的必由之路．当前随着新一轮科技革命和产业变革孕育兴起，新能源汽车产业正进入加速发展的新阶段，下列图案是我国的一些国产新能源车企的车标，图案既是轴对称图形，又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 抛物线y=（x﹣2）²+3的顶点坐标是（）

A、（﹣2，3） B、（2，3） C、（﹣2，﹣3） D、（2，﹣3）

查看试题解析
3. 方程 $x (x - 2) = 0$ 的解是（）.

A、 $x = 0$ B、 $x = 2$ C、 $x_{1} = 0$ ， $x_{2} = 2$ D、 $x = \pm 2$

查看试题解析
4. 由抛物线y＝2x² ．平移而得到抛物线y＝2（x－1）²－2，下列平移正确的是（）

A、先向左平移1个单位，再向上平移2个单位 B、先向左平移1个单位，再向下平移2个单位 C、先向右平移1个单位，再向上平移2个单位 D、先向右平移1个单位，再向下平移2个单位

查看试题解析
5. 下列说法，正确的是（）

A、等弦所对的圆周角相等 B、弦所对的两条弧的中点的连线垂直平分弦，且过圆心 C、切线垂直于圆的半径 D、平分弦的直径垂直于弦

查看试题解析
6. 如图，△ADE旋转到△CDB，点A与点C是对应点，下列说法错误的是（）

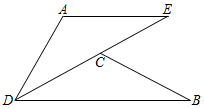A、AE∥BD B、AD＝DC C、DE平分∠ADB D、AE＝BC

查看试题解析
7. 设 $A (0 ， y_{1})$ ， $B (1 ， y_{2})$ ， $C (2 ， y_{3})$ 是抛物线 $y = - {(x + 1)}^{2} + k$ 上的三点，则 $y_{1} ， y_{2} ， y_{3}$ 的大小关系为（）

A、 $y_{3} > y_{2} > y_{1}$ B、 $y_{1} > y_{3} > y_{2}$ C、 $y_{1} > y_{2} > y_{3}$ D、 $y_{3} > y_{1} > y_{2}$

查看试题解析
8. 如图，⊙O的直径AB垂直于弦CD，∠CAB=36°，则∠BCD的大小是（）

A、18° B、36° C、54° D、72°

查看试题解析
9. 如图，四边形 $A B C D$ 内接于 $⊙ O$ ．若 $∠ B = 108 °$ ，则 $∠ D$ 的大小为（）

A、 $54 °$ B、 $62 °$ C、 $72 °$ D、 $82 °$

查看试题解析
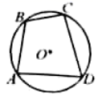10. 二维码已经给我们的生活带来了很大方便，它是由大小相同的黑白两色的小正方形（如图1中C）按某种规律组成的一个大正方形，现有25×25格式的正方形如图1，角上是三个7×7的A型大黑白相间正方形，中间右下一个5×5的B型黑白相间正方形，除这4个正方形外，若其他的小正方形白色块数y与黑色块数x正好满足如图2所示的函数图象，则该25×25格式的二维码共有多少块黑色的C型小正方形（）

A、153 B、218 C、100 D、216

查看试题解析

二、填空题

11. 大小、形状完全相同的5张卡片，背面分别写着“我”“的”“中”“国”“梦”这5个字，从中随机抽取一张，则这张卡片背面恰好写着“中”字的概率是．

查看试题解析
12. 已知，点 $A (x ， - 5)$ ， $B (1 ， y)$ 关于原点对称，则 $x + y$ 的值为．

查看试题解析
13. 半径是2的圆，如果半径增加x时，增加的面积s与x之间的关系表达式为.

查看试题解析
14. 已知x₁ ， x₂是一元二次方程x²﹣2x﹣1=0的两根，则 $\frac{1}{x_{1}} + \frac{1}{x_{2}}$ =

查看试题解析
15. 扇形的半径为3，圆心角为90°，则该扇形的面积为.（结果保留 $π$ ）

查看试题解析
16. 已知抛物线 $y = x^{2} + b x + c$ 的部分图象如图所示，则方程 $x^{2} + b x + c = 0$ 的解是

查看试题解析
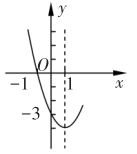17. 如图，圆O的半径为2.C₁是函数y=x²的图象，C₂是函数y=−x²的图象，则阴影部分的面积是.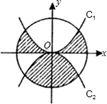

查看试题解析

三、计算题

18. 解方程：

(1)、2x²+1=3x（配方法）

(2)、(2x-1)²=(3-x)²（因式分解法）

查看试题解析
19. 已知二次函数的图象经过（－6，0），（2，0），（0，－6）三点．

(1)、求这个二次函数的表达式；

(2)、求这个二次函数的顶点坐标．

查看试题解析

四、解答题

20. 如图，平面直角坐标系中，点D坐标为 $(0 ， 1)$ ，每个小正方形网格的顶点叫做格点， $▱ A B C D$ 的顶点均在格点上，仅用无刻度直尺在给定网格中按要求作图．作图过程用虚线表示，作图结果用实线表示．

(1)、将线段 $A D$ 绕点A逆时针旋转 $90 °$ ，画出对应线段 $A E$ ，并直接写出点E的坐标 ▲ ．

(2)、过（1）中的点E画一条直线把平行四边形 $A B C D$ 分成面积相等的两部分．

查看试题解析
21. 已知关于x的方程 $k^{2} x^{2} - 2 (k + 1) x + 1 = 0$ 有两个实数根．

(1)、求k的取值范围．

(2)、若k为符合条件的最小整数，求此方程的根．

查看试题解析
22. 模拟经过某十字路口的汽车，它可能继续直行，也可能向左转或向右转，如果这三种情况是等可能的，当同向行驶的三辆汽车经过这个十字路口时，

(1)、求三辆车全部同向而行的概率．

(2)、求至少有两辆车向左转的概率．

(3)、这个路口汽车左转．右转、直行的指示绿灯交替亮起，亮的时间均为30秒．交管部门对这个十字路口交通高峰时段车流量作了统计，发现汽车在此十字路口向右转的频率为 $\frac{2}{5}$ ，向左转和直行的频率均为 $\frac{3}{10}$ ，在绿灯亮的总时间不变的条件下，为使交通更加通畅，请你用统计的知识对此十字路口三个方向的绿灯亮的时间做出合理的调整．

查看试题解析
23. 某水产经销商以每千克30元的价格购进一批某品种淡水鱼，由销售经验可知，这种淡水鱼的日销售量y（千克）与销售价格x（元/千克）（30≤x＜60）存在一次函数关系，部分数据如表所示：
销售价格x（元/千克）
50
40
日销售量y（千克）
100
200

(1)、试求出y关于x的函数表达式．

(2)、设该经销商销售这种淡水鱼的日销售利润为W元，如果不考虑其他因素，求当销售价格x为多少时，日销售利润W最大？最大的日销售利润是多少元？

查看试题解析
24. 如图，AB是⊙O的直径，AD平分∠BAC，交⊙O于点D，过点D作直线DE⊥AC，交AC的延长线于点E，交AB的延长线于点F．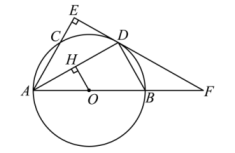

(1)、求证：EF是⊙O的切线；

(2)、过点O作OH⊥AD，交AD于点H，连接BD，若BD=6，AH=3 $\sqrt{3}$ ，则⊙O的半径=

查看试题解析
25. 如图1，在平面直角坐标系xOy中，二次函数y＝x²-4x+c的图象与y轴的交点坐标为（0，5），图象的顶点为M ．矩形ABCD的顶点D与原点O重合，顶点A ， C分别在x轴，t轴上，顶点B的坐标为（1，5）．

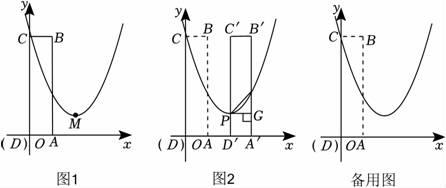(1)、求c的值及顶点M的坐标．

(2)、如图2，将矩形ABCD沿x轴正方向平移t个单位（0＜t＜3）得到对应的矩形A′B′C′D′．已知边C′D′，A′B′分别与函数y＝x²-4x+c的图象交于点P ， Q ，连结PQ ，过点P作PG⊥A′B′于点G ．
①当t＝2时，求QG的长；
②当点G与点Q不重合时，是否存在这样的t ，使得△PGQ的面积为1？若存在，求出此时t的值；若不存在，请说明理由．

查看试题解析

销售价格x（元/千克）	50	40
日销售量y（千克）	100	200