人教版（贵州地区）初中数学2023-2024学年八年级上学期期末模拟卷（三）

试卷更新日期：2023-12-18 类型：期末考试

进入出卷网下载

一、选择题

1. 下列交通标志的图案是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 使分式 $\frac{x}{x - 3}$ 有意义的条件是（）

A、 $x = 0$ B、 $x \neq 0$ C、 $x \neq 3$ D、 $x = 3$

查看试题解析
3. 计算： a⁶÷a⁴=（）

A、a² B、a³ C、a⁴ D、a⁵

查看试题解析
4. 下列式子从左到右的变形，属于因式分解的是（）

A、 $(x + 1) (x - 1) = x^{2} - 1$ B、 $x^{2} + 2 x - 1 = x (x + 2) - 1$ C、 $a^{2} b + a b^{2} = a b (a + b)$ D、 $a (a + b) = a^{2} + a b$

查看试题解析
5. 如图的两个三角形全等，则 $∠ 1$ 的度数为（）

A、50° B、58° C、60° D、62°

查看试题解析
6. 在△ABC中，若∠A=∠B=2∠C，则△ABC的形状是（）

A、锐角三角形 B、直角三角形 C、钝角三角形 D、无法确定

查看试题解析
7. 一个凸多边形的内角和比它的外角和的 3 倍还多 180°，则这个多边形是（）

A、九边形 B、八边形 C、七边形 D、六边形

查看试题解析
8. 如图，已知 $△ A B C ≌ △ E D F$ ，点 $A ， E ， C ， F$ 在同一直线上，延长 $B C$ 交 $D F$ 边于点 $M$ ．若 $∠ B A C = 70 ° ， ∠ E D F = 62 °$ ，则 $∠ M C F$ 的度数为（）

A、 $38 °$ B、 $48 °$ C、 $62 °$ D、 $70 °$

查看试题解析
9. 有下列说法：
①能够重合的两个三角形是全等三角形；②全等三角形的对应边相等；③全等三角形的对应角相等；④全等三角形的周长相等，面积相等．其中正确的是（）

A、①②③ B、①②④ C、②③④ D、①②③④

查看试题解析
10. 如图，小明把一张边长为10厘米的正方形硬纸板的四周各剪去一个同样大小的小正方形（该小正方形的边长为m厘米），再按虚线折叠，制成一个无盖的长方体盒子，则该长方体盒子的体积可表示为（）立方厘米．

A、 $- 4 m^{3} + 100 m$ B、 $4 m^{3} - 40 m^{2} + 100 m$ C、 $- 2 m^{3} + 10 m^{2}$ D、 $4 m^{3} + 20 m^{2} + 100$

查看试题解析
11. 如图，点 $A ， E ， F ， C$ 在同一直线上， $B F ⊥ A C$ 于点 $F ， D E ⊥ A C$ 于点 $E$ ，连结 $B D$ ，交 $E F$ 于点 $O$ ，且 $O$ 为 $E F$ 的中点．若 $A E = C F$ ，则下列结论：① $△ E O D ≌ △ F O B$ ；② $A O = C O$ ；③ $A B = C D$ ；④ $A B / / C D$ ，其中正确的是（）

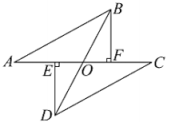A、①② B、③④ C、①②③ D、①②③④

查看试题解析
12. 我们学习多边形后，发现凸多边形的对角线有一定的规律，①中的四边形共有2条对角线，②中的五边形共有5条对角线，③中的六边形共有9条对角线，…，请你计算凸十边形对角线的总条数（　　）

A、54 B、44 C、35 D、27

查看试题解析

二、填空题

13. 在平面直角坐标系中，点 $(m ， - 2)$ 与点 $(3 ， n)$ 关于x轴对称，则 $m + n =$ ．

查看试题解析
14. 等腰三角形的两边长分别为8，6，这个三角形的周长为．

查看试题解析
15. 如图，在△ABC中，D是BC延长线上一点，∠B=40°，∠ACD= 120，则∠A= °.

查看试题解析
16. 如图所示，等边△ABC中，B点在坐标原点，C点坐标为（4，0），点A关于x轴对称点A′的坐标为．

查看试题解析
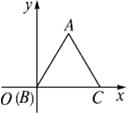17. 如图，AD是△ABC的角平分线，BE是△ABC的高，∠BAC＝40°，则∠AFE的度数为.

查看试题解析
18. 如图，等腰三角形ABC底边BC的长为 4cm，面积是12cm² ，腰 AB的垂直平分线EF交AC于点F，若 D为 BC边上的中点，M为线段EF上一动点，则△BDM的周长最短为cm.

查看试题解析

三、计算题

19. 计算题

(1)、 $3 (4 x - 3) - (5 x - 6)$ ；

(2)、 $(25 x^{2} + 15 x^{3} y - 20 x^{4}) \div (- 5 x^{2})$ .

查看试题解析
20. 解方程：

(1)、 $\frac{1}{x - 2}$ ＋2＝ $\frac{1 - x}{2 - x}$

(2)、 $\frac{1 - 3 x}{1 + 3 x} + \frac{3 x + 1}{3 x - 1} = \frac{12}{1 - 9 x^{2}}$

查看试题解析
21. 将下列多项式分解因式：

(1)、3a²-6ab+3b²；

(2)、x²（m-2）+y²（2 -m）

查看试题解析
22. 先化简，再求值： $(\frac{x + 2}{x} - \frac{x - 1}{x - 2}) \div \frac{x - 4}{x^{2} - 4 x + 4}$ ，其中 $x = - 1$ .

查看试题解析

四、综合题

23. 如图，在长度为1个单位长度的小正方形组成的正方形网格中， $△$ ABC的三个顶点A、B、C都在格点上．

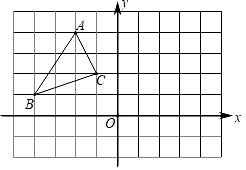
（ 1 ）在图中画出与 $△$ ABC关于直线y成轴对称的 $△$ A₁B₁C₁；

（ 2 ）求 $△$ ABC的面积；

（ 3 ）在x轴上找出一点P，使得PB+PC的值最小．（不需计算，在图上直接标记出点P的位置）

查看试题解析

五、实践探究题

24. [问题情境]
在综合实践课上，老师组织班上的同学开展了探究两角之间数量关系的数学活动，如题24图，已知射线AM∥BN，连接AB，点P是射线AM上的一个动点(与点A不重合)，BC，BD分别平分∠ABP和∠PBN，且分别交射线AM于点C，D．
[探索发现]

(1)、当∠A=60°时，求证：∠CBD=∠A．

(2)、”快乐小组”经过探索后发现：不断改变∠A的度数，∠CBD与∠A始终存在某种数量关系．
①当∠A=40°时，∠CBD=度；
②当∠A=x°时，∠CBD=度(用含x的代数式表示)．

(3)、[操作探究]
”智慧小组”利用量角器量出∠APB和∠ADB的度数后，探究二者之间的数量关系．他们惊奇地发现，当点P在射线AM上运动时，无论点P在AM上的什么位置，∠APB与∠ADB之间的数量关系都保持不变．请写出它们的关系，并说明理由．

查看试题解析