人教版(贵州地区)初中数学2023-2024学年八年级上学期期末模拟卷(二)
试卷更新日期:2023-12-18 类型:期末考试
一、选择题
-
1. 计算(-2a2)3的结果是( )A、-6a6 B、-8a6 C、6a5 D、-8a52. 下列运算结果正确的是( )A、 B、 C、 D、3. 下列计算正确的是( )A、 B、 C、 D、4. 若分式的值为零,则x的值是( )A、 B、0 C、1 D、25. 如图,的边上的高是( )
 A、线段 B、线段 C、线段 D、线段6. 某校美术社团为练习素描,他们第一次用120元买了若干本资料,第二次用240元在同一商家买同样的资料,这次商家每本优惠4元,结果比上次多买了20本.求第一次买了多少本资料?若设第一次买了x本资料,列方程正确的是( )A、 B、 C、 D、7. 如图,小峰从点O出发,前进8m后向右转40°,再前进8m后又向右转40°,…,这样一直走下去,他第一次回到出发点O时,走的路程一共是( )m.
A、线段 B、线段 C、线段 D、线段6. 某校美术社团为练习素描,他们第一次用120元买了若干本资料,第二次用240元在同一商家买同样的资料,这次商家每本优惠4元,结果比上次多买了20本.求第一次买了多少本资料?若设第一次买了x本资料,列方程正确的是( )A、 B、 C、 D、7. 如图,小峰从点O出发,前进8m后向右转40°,再前进8m后又向右转40°,…,这样一直走下去,他第一次回到出发点O时,走的路程一共是( )m.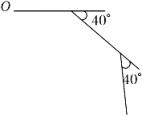 A、72 B、56 C、32 D、168. 如图,在一块长 , 宽的长方形空地上,修建同样宽的两条互相垂直的道路两条道路各与长方形的一条边垂直 , 剩余部分栽种花草美化环境,设道路的宽度为 , 则栽种花草的面积表示不正确的是( )
A、72 B、56 C、32 D、168. 如图,在一块长 , 宽的长方形空地上,修建同样宽的两条互相垂直的道路两条道路各与长方形的一条边垂直 , 剩余部分栽种花草美化环境,设道路的宽度为 , 则栽种花草的面积表示不正确的是( )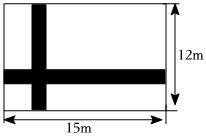 A、 B、 C、 D、9. 若关于x的分式方程无解,则k的取值是( )A、 B、或 C、 D、或10. 中, , 和的平分线交于点 , 得;和的平分线交于点 , 得和的平分线交于点 , 则为( )
A、 B、 C、 D、9. 若关于x的分式方程无解,则k的取值是( )A、 B、或 C、 D、或10. 中, , 和的平分线交于点 , 得;和的平分线交于点 , 得和的平分线交于点 , 则为( )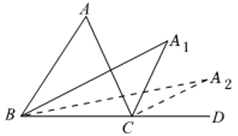 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 因式分解:3x3-12x= .12. 若am=2,an=3,则am+n等于13. 长分别为11,8,6,4的四根木条,选其中三根组成三角形种选法.14. 关于x的分式方程的解为正数,则m的取值范围是 .15. 如图,分别是的高和角平分线,若 , , 则的度数为 .
 16. 如图,点D是BC的中点,若△ABC的面积为6,则△ADC的面积为 .
16. 如图,点D是BC的中点,若△ABC的面积为6,则△ADC的面积为 .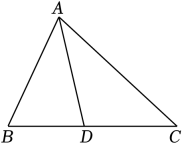 17. 若分式方程有增根,则a的值为 .18. 一个多边形的内角和等于它的外角和的倍,则这个多边形的边数是 .
17. 若分式方程有增根,则a的值为 .18. 一个多边形的内角和等于它的外角和的倍,则这个多边形的边数是 .三、计算题
-
19. 因式分解(1)、 ;(2)、 .20. 解方程:(1)、(2)、
四、解答题
-
21. 如图,在平面直角坐标系中,A(0,1),B(﹣2,3),C(4,4).
 (1)、在图中作出△ABC关于x轴的对称图形△A′B′C′;
(1)、在图中作出△ABC关于x轴的对称图形△A′B′C′;
(2)、写出△A′B′C′三个顶点的坐标.22. 如图,BD是△ABC的高线,∠A=60°,∠C=50°.求∠ABD与∠CBD的度数. 23. 如图,在中,是边上的高线,是一条角平分线,它们相交于点P.已知 , , 求的度数.
23. 如图,在中,是边上的高线,是一条角平分线,它们相交于点P.已知 , , 求的度数. 24. 如图,P为等边△ABC内一点,连接BP、PC,延长PC到点D,使CD= PC;延长BC到点E,使CE=BC,连接AE、DE.
24. 如图,P为等边△ABC内一点,连接BP、PC,延长PC到点D,使CD= PC;延长BC到点E,使CE=BC,连接AE、DE. (1)、求证:BP∥DE;(2)、求∠BAE的度数;(3)、若BP⊥AC,则∠AED=度.
(1)、求证:BP∥DE;(2)、求∠BAE的度数;(3)、若BP⊥AC,则∠AED=度.五、实践探究题
-
25. 定义:在任意中,如果一个内角度数的2倍与另一个内角度数的和为 , 那么称此三角形为“倍角互余三角形”.
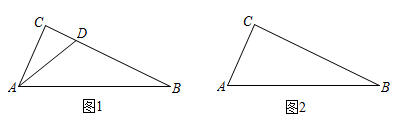 (1)、【基础巩固】若是“倍角互余三角形”, , , 则;(2)、【尝试应用】如图1,在中, , 点为线段上一点,若与互余.求证:是“倍角互余三角形”;(3)、【拓展提高】如图2,在中, , , , 试问在边上是否存在点 , 使得是“倍角互余三角形”?若存在,请求出的长;若不存在,请说明理由.
(1)、【基础巩固】若是“倍角互余三角形”, , , 则;(2)、【尝试应用】如图1,在中, , 点为线段上一点,若与互余.求证:是“倍角互余三角形”;(3)、【拓展提高】如图2,在中, , , , 试问在边上是否存在点 , 使得是“倍角互余三角形”?若存在,请求出的长;若不存在,请说明理由.