贵州省贵阳市花溪区2023-2024学年九年级上学期期中数学试卷

试卷更新日期：2023-12-18 类型：期中考试

进入出卷网下载

一、选择题（每小题3分，共36分.以下每小题均有A、B、C、D四个选项，其中只有

1. 一元二次方程3x²﹣5x﹣3＝0的一次项系数是（　　）

A、3 B、﹣5 C、﹣3 D、0

查看试题解析
2. 如图，在矩形 $A B C D$ 中，对角线 $A C$ 与 $B D$ 相交于点 $O$ ，已知 $∠ A C B = 25 °$ ，则 $∠ A O B$ 的大小是（）

A、 $130 °$ B、 $65 °$ C、 $50 °$ D、 $25 °$

查看试题解析
3. 《九章算术》中注有“今有两数，若其意义相反，则分别叫做正数与负数．”若盈利200元记作+200元，则﹣200元表示（　　）

A、亏损200元 B、盈利200元 C、亏损﹣200元 D、不盈利不亏损

查看试题解析
4. 甲骨文是我国目前发现最早的文字，其显著特点是图画性强，下列甲骨文图画是轴对称图形的是（　　）

A、 B、 C、 D、

查看试题解析
5. 两三角形的相似比是2：3，则其面积之比是（）

A、 $\sqrt{2}$ ： $\sqrt{3}$ B、2：3 C、4：9 D、8：27

查看试题解析
6. 将一元二次方程（x﹣6）²＝25转化为两个一元一次方程，其中一个一元一次方程是x﹣6＝5，则另一个一元一次方程是（　　）

A、x﹣6＝﹣5 B、x﹣6＝5 C、x+6＝﹣5 D、x+6＝5

查看试题解析
7. 如图，正方形ABCD的边长为1，点E，F分别是对角线AC上的两点，EG⊥AB．EI⊥AD，FH⊥AB，FJ⊥AD，垂足分别为G，I，H，J．则图中阴影部分的面积等于（）

A、1 B、 $\frac{1}{2}$ C、 $\frac{1}{3}$ D、 $\frac{1}{4}$

查看试题解析
8. 一元二次方程x²﹣2x=0的两根分别为x₁和x₂ ，则x₁x₂为（　　）

A、﹣2 B、1 C、2 D、0

查看试题解析
9. 从“数学”的英文单词“mathematics”中随机抽取一个字母，抽中字母m的概率为（　　）

A、 $\frac{1}{6}$ B、 $\frac{1}{4}$ C、 $\frac{1}{5}$ D、 $\frac{2}{11}$

查看试题解析
10. 一元二次方程2x²﹣5x+6＝0的根的情况为（　　）

A、有两个不等的实数根 B、无实数根 C、有两个相等的实数根 D、无法判定

查看试题解析
11. 如图，在菱形ABCD中，E是AC的中点，EF∥CB，交AB于点F，如果EF=3，那么菱形ABCD的周长为（　　）

A、24 B、18 C、12 D、9

查看试题解析
12. 定义：关于x的一元二次方程： $a_{1} (x - m)^{2} + n = 0$ 与 $a_{2} (x - m)^{2} + n = 0$ ，称为“同族二次方程”．如2（x﹣3）²+4＝0与3（x﹣3）²+4＝0是“同族二次方程”．若关于x的一元二次方程：2（x﹣1）²+1＝0与（a+2）x²+（b﹣4）x+8＝0是“同族二次方程”．则代数式﹣ax²+bx+2019的最大值是（　　）

A、2024 B、2023 C、2022 D、2021

查看试题解析

二、填空题（每小题4分。共16分）

13. 若关于x的一元二次方程x²+mx+n＝0有一个根是1，则m+n＝．

查看试题解析
14. 田大伯为与客户签订销售合同，需了解自己鱼塘里鱼的数量，为此，他从鱼塘先捞出200条鱼做上标记再放入鱼塘，经过一段时间后又捞出300条，发现有标记的鱼有20条，则田大伯的鱼塘里鱼的条数是．

查看试题解析
15. 在“一圈两场三改”活动中，某小区计划在一块长为32m，宽为20m的矩形场地上修建三条同样宽且互相垂直的小路，剩余的空地上种植草坪．根据规划，小路分成的六块草坪总面积为570m²（如图所示）．求小路的宽为多少米？若设小路的宽为x m，根据题意所列方程是．

查看试题解析
16. 如图，在边长为2的正方形 $A B C D$ 中，E，F分别是 $B C ， C D$ 上的动点，M，N分别是 $E F ， A F$ 的中点，则 $M N$ 的最大值为．

查看试题解析

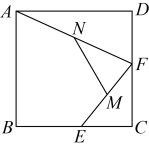
三、解答题（本大题7小题，共48分.解答应写出必要的文字说明，证明过程或演算步骤.）

17. 用适当方法解下列方程．

(1)、x²﹣9＝0；

(2)、x²﹣4x+3＝0．

查看试题解析
18. 如图，点E是平行四边形ABCD的边BC延长线上一点，连接AE，交CD于点F．写出图中任意一对相似三角形，并说明理由．

查看试题解析
19. 列方程解应用题：
某玩具厂生产一种玩具，按照控制固定成本降价促销的原则，使生产的玩具能够及时售出，据市场调查：每个玩具按480元销售时，每天可销售160个；若销售单价每降低1元，每天可多售出2个，已知每个玩具的固定成本为360元，问这种玩具的销售单价为多少元时，厂家每天可获利润20000元？

查看试题解析
20. 在一个不透明的盒子中装有2个红球，1个黄球，它们除颜色外，其余都相同．小明和小英做摸球游戏，约定游戏规则是：小英先从中随机摸出一个球，记下颜色后放回摇匀，小明再从中随机摸出一个球．如果两人摸到球的颜色相同，小英赢，否则小明赢．

(1)、请用树状图或列表格法表示一次游戏中所有可能出现的结果；

(2)、这个游戏规则公平吗？请说明理由．

查看试题解析
21. 如图，点E是矩形ABCD的边BC上的一点，且AE=AD．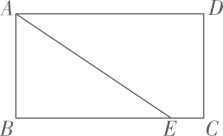

(1)、尺规作图（请用2B铅笔）：作∠DAE的平分线AF，交BC的延长线于点F，连接DF．（保留作图痕迹，不写作法）；

(2)、试判断四边形AEFD的形状，并说明理由．

查看试题解析
22. 小明用一根长56厘米的铁丝围一个矩形．

(1)、当矩形面积为180平方厘米时，长、宽分别是多少？

(2)、他还能用这根铁丝围成面积为200平方厘米的矩形吗？说明理由．

查看试题解析
23. 【综合与实践】
定义：对角线互相垂直的四边形叫做垂美四边形．如图①所示的四边形ABCD是垂美四边形．

(1)、【概念理解】
①正方形，②菱形，③矩形，三个图形中一定是垂美四边形的是；（填序号）

(2)、【性质探究】
小明说：在如图①的垂美四边形ABCD中AD²+BC²＝AB²+CD² ，请你判断他的说法是否正确，并说明理由；

(3)、【问题解决】
如图②，分别以Rt△ABC的直角边AC和斜边AB为边向外作正方形ACFG和正方形ABDE，连接CE交AB于点M，连接BG交CE于点N，连接GE．已知AC＝4，AB＝5，求GE的长．

查看试题解析