河北省唐山市路北区2023-2024学年九年级上学期期中数学试卷

试卷更新日期：2023-12-18 类型：期中考试

进入出卷网下载

一、选择题（本大题有14个小题，每题2分，共28分.在每小题给出的四个选项中，只有一项是符合题目要求的）

1. 抛物线y＝x²开口方向（　　）

A、向上 B、向下 C、向左 D、向右

查看试题解析
2. 关于x的一元二次方程（m﹣3）x²+m²x＝9x+5化为一般形式后不含一次项，则m的值为（　　）

A、0 B、±3 C、3 D、﹣3

查看试题解析
3. 如图，AB是⊙O的直径，AC，BC是⊙O的弦，若 $∠ A = 20 °$ ，则 $∠ B$ 的度数为（）

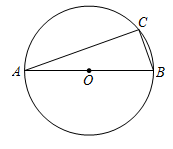A、70° B、90° C、40° D、60°

查看试题解析
4. 抛物线y＝（x+5）（x﹣3）的对称轴是直线（　　）

A、x＝﹣5 B、x＝﹣1 C、x＝1 D、x＝3

查看试题解析
5. 如图，点A ， B ， C均在⊙O上，若∠A＝68°，则∠OCB＝（　　）

A、22° B、23° C、24° D、28°

查看试题解析
6. 若关于x的一元二次方程x²+6x+c＝0配方后得到方程（x+3）²＝2c，则c的值为（　　）

A、﹣3 B、0 C、3 D、9

查看试题解析
7. 形状与抛物线y＝﹣x²+2相同，并且图象有最低点，则抛物线可能是将（　　）

A、y＝x²+5x+6 B、y＝﹣x²﹣5x+6 C、y＝﹣x²+5x+6 D、y＝x²+5x+6或y＝﹣x²﹣5x+6

查看试题解析
8. 关于x的一元二次方程x²﹣2x+m﹣2＝0有两个不相等的实数根，则m的取值范围是（　　）

A、 $m < \frac{3}{2}$ B、m＞3 C、m≤3 D、m＜3

查看试题解析
9. 如图，四边形ABCD是⊙O的内接四边形，若∠AOC＝160°，则∠ABC的度数是（）

A、80° B、100° C、140° D、160°

查看试题解析
10. 有一个人患了流行性感冒，经过两轮传染后共有144人患了流行性感冒，则每轮传染中平均一个人传染的人数是（）

A、14 B、11 C、10 D、9

查看试题解析
11. 在⊙O中 $\overset{⌢}{A B} = 2 \overset{⌢}{C D}$ ，则弦AB与弦CD的大小关系是（　　）

A、AB＞2CD B、AB＝2CD C、AB＜2CD D、AB＝CD

查看试题解析
12. 如图，二次函数y＝ax²+bx+c的图象经过点A（1，0），B（5，0），下列说法正确的是（）

A、c＜0 B、b²-4ac＜0 C、a-b+c＜0 D、图象的对称轴是直线x＝3

查看试题解析
13. 如图，AB是⊙O的直径，C，D是⊙O上的两点，且BC平分∠ABD，AD分别与BC，OC相交于点E，F，则下列结论不一定成立的是（　　）

A、OC∥BD B、AD⊥OC C、△CEF≌△BED D、AF＝FD

查看试题解析
14. 已知P₁（x₁ ， y₁），P₂（x₂ ， y₂）是抛物线y＝ax²﹣2ax上的点，下列命题正确的是（）

A、若|x₁﹣1|＞|x₂﹣1|，则y₁＞y₂ B、若|x₁﹣1|＞|x₂﹣1|，则y₁＜y₂ C、若|x₁﹣1|＝|x₂﹣1|，则y₁＝y₂ D、若y₁＝y₂ ，则x₁＝x₂

查看试题解析

二、填空题（本大题有4个小题，每小题3分，共12分）

15. 已知一元二次方程x²﹣4x+m＝0的一个根为x₁＝1．则另一个根x₂＝．

查看试题解析
16. 如图，某博览会上有一圆形展示区，在其圆形边缘的点 $P$ 处安装了一台监视器，它的监控角度是 $55 °$ ，为了监控整个展区，最少需要在圆形边缘上共安装这样的监视器台．

查看试题解析
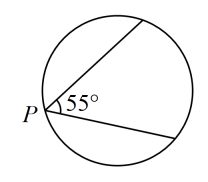17. 将二次函数y＝x²﹣4x+a的图象向左平移1个单位，再向上平移1个单位，若得到的函数图象与直线y＝2有两个交点，则a的取值范围是.

查看试题解析
18. 如图， $C D$ 为 $⊙ O$ 的直径，弦 $A B ⊥ C D$ ，垂足为 $E$ ， $\overset{⌢}{A B} = \overset{⌢}{B F}$ ， $C E = 1$ ， $A B = 6$ ，则弦 $A F$ 的长度为.

查看试题解析

三、解答题（本大题有8道小题，共60分）

19. 计算

(1)、用配方法解方程：x²﹣4x﹣32＝0；

(2)、用公式法解方程：2x²+3＝6x ．

查看试题解析
20. 已知二次函数y＝ax²+bx+3，几组该函数x与y的对应值如表：
x
…
﹣1
1
2
…
y
…
0
m
3
…

(1)、求此二次函数的解析式；

(2)、求m的值．

查看试题解析
21. 已知关于x的一元二次方程x²﹣ax+a﹣1＝0．

(1)、求证：该方程总有两个实数根；

(2)、若该方程其中一根是负整数，且a是非负数，求a的值．

查看试题解析
22. 如图1，装有水的水槽放置在水平桌面上，其横截面是以AB为直径的半圆O ， AB＝52cm ， MN为水面截线，MN＝48cm ， GH为桌面截线，MN∥GH ．

(1)、作OC⊥MN于点C ，求OC的长；

(2)、将图中的水倒出一部分得到图2，发现水面高度下降了14cm ，求此时水面截线减少了多少．

查看试题解析
23. 某校团体操表演队伍有6行8列，后又增加了51人，使得团体操表演队伍增加的行、列数相同，求增加了多少行或多少列？

查看试题解析
24. 掷实心球是某市中考体育考试的选考项目．已知一名男生投实心球行进路线是一条抛物线，行进高度y（m）与水平距离x（m）之间的函数关系如图所示，掷出时起点处高度为2m ，当水平距离为 $\frac{9}{2} m$ 时，实心球行进至最高点 $\frac{25}{8} m$ 处．

(1)、求y关于x的函数解析式；

(2)、根据该市2023年中考体育考试评分标准（男生），投掷过程中，实心球从起点到落地点的水平距离不小于12.4m ，此项考试得分为满分17分．按此评分标准，该生在此项考试中是否得满分，请说明理由．

查看试题解析
25. 已知二次函数y＝﹣x²+bx+c ．

(1)、当该函数对称轴是直线x＝2，且过点（0，3）．
①求该函数的解析式，并直接写出顶点坐标；
②当﹣1≤x≤3时，直接写出y的取值范围；

(2)、当x≤0时，y的最大值为2；当x＞0时，y的最大值为3，求二次函数的表达式．

查看试题解析
26. 如图1，在平面直角坐标系中，正方形OABC的边长为4，边OA ， OC分别在x轴，y轴的正半轴上，把正方形OABC的内部及边上，横、纵坐标均为整数的点称为好点．点P为抛物线y＝﹣（x﹣m）²+m+2的顶点．

(1)、直接写出顶点P的坐标；（用m表示）

(2)、当m＝0时，判断（1，1）是否在抛物线上，并直接写出该抛物线下方（含边界）的好点个数；

(3)、当m＝3时，直接写出该抛物线上的好点坐标；

(4)、若点P在正方形OABC内部，该抛物线下方（含边界）恰好存在8个好点，直接写出m的取值范围．

查看试题解析

x	…	﹣1	1	2	…
y	…	0	m	3	…