四川省德阳市中江县2022-2023学年七年级下学期数学第一次月考考试试卷
试卷更新日期:2023-12-18 类型:月考试卷
一、选择题(本大题共12个小题,每题4分,满分48分)在每小题给出的四个选项中,有且仅有一项是符合题目要求的。
-
1. 图中,∠1和∠2是对顶角的是( )A、
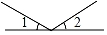 B、
B、 C、
C、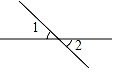 D、
D、 2. 2022年,中国举办了第二十四届冬季奥林匹克运动会,如图,通过平移右图吉祥物“冰墩墩”可以得到的图形是( )
2. 2022年,中国举办了第二十四届冬季奥林匹克运动会,如图,通过平移右图吉祥物“冰墩墩”可以得到的图形是( ) A、
A、 B、
B、 C、
C、 D、
D、 3. 下列定理中,下面语句是命题的是( )A、π是有理数 B、已知a=3,求a3 C、作∠ABC的角平分线 D、正数大于一切负数吗?4. 如图,两条平行线a , b被第三条直线c所截.若∠2=58°,则∠1的度数为( )
3. 下列定理中,下面语句是命题的是( )A、π是有理数 B、已知a=3,求a3 C、作∠ABC的角平分线 D、正数大于一切负数吗?4. 如图,两条平行线a , b被第三条直线c所截.若∠2=58°,则∠1的度数为( )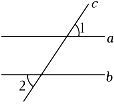 A、120° B、112° C、124° D、58°5. 下列语句正确的是( )A、的立方根是2 B、﹣3是27的立方根 C、(﹣1)2的立方根是﹣1 D、的立方根是6. 如图,若∠2=31°,则∠1的度数是( )
A、120° B、112° C、124° D、58°5. 下列语句正确的是( )A、的立方根是2 B、﹣3是27的立方根 C、(﹣1)2的立方根是﹣1 D、的立方根是6. 如图,若∠2=31°,则∠1的度数是( )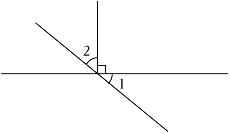 A、31° B、59° C、49° D、69°7. 春节过后,某村计划挖一条水渠将不远处的河水引到农田(记作点O),以便对农田的小麦进行灌溉,现设计了四条路段OA , OB , OC , OD , 如图所示,其中最短的一条路线是( )
A、31° B、59° C、49° D、69°7. 春节过后,某村计划挖一条水渠将不远处的河水引到农田(记作点O),以便对农田的小麦进行灌溉,现设计了四条路段OA , OB , OC , OD , 如图所示,其中最短的一条路线是( )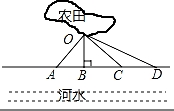 A、OA B、OB C、OC D、OD8. 如图,下列说法中,正确的是( )
A、OA B、OB C、OC D、OD8. 如图,下列说法中,正确的是( )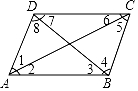 A、若∠3=∠8,则AB∥CD B、若∠1=∠5,则AB∥CD C、若∠DAB+∠ABC=180°,则AB∥CD D、若∠2=∠6,则AB∥CD9. 下列说法中,错误的是( )
A、若∠3=∠8,则AB∥CD B、若∠1=∠5,则AB∥CD C、若∠DAB+∠ABC=180°,则AB∥CD D、若∠2=∠6,则AB∥CD9. 下列说法中,错误的是( )①a与c相交,b与c相交,则a与b相交;
②若a∥b , b∥c , 则a∥c;
③过直线外一点有且只有一条直线与已知直线平行;
④在同一平面内,两条直线的位置关系平行、相交、垂直三种.
A、3个 B、2个 C、1个 D、0个10. 如图,∠1=60°,下列推理正确的是( )①若∠2=60°,则AB∥CD;②若∠5=60°,则AB∥CD;
③若∠3=120°,则AB∥CD;④若∠4=120°,则AB∥CD .
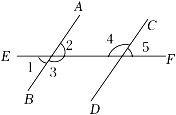 A、①② B、②④ C、②③④ D、②③11. 2022年北京冬奥会男子500米短道速滑冠军高亭玉在一次速滑训练中,经过两次拐弯后的速滑方向与原来的方向相反,则两次拐弯的角度可能是( )
A、①② B、②④ C、②③④ D、②③11. 2022年北京冬奥会男子500米短道速滑冠军高亭玉在一次速滑训练中,经过两次拐弯后的速滑方向与原来的方向相反,则两次拐弯的角度可能是( ) A、第一次向左拐52°,第二次向右拐52° B、第一次向左拐48°,第二次向左拐48° C、第一次向左拐73°,第二次向右拐107° D、第一次向左拐32°,第二次向左拐148°12. 如图,将一副三角板按如图放置,则下列结论:①∠1=∠3;②∠CAD+∠2=180°;③如果∠2=35°,则有BC∥AD;④∠4+∠2=75°.其中正确的序号是( )
A、第一次向左拐52°,第二次向右拐52° B、第一次向左拐48°,第二次向左拐48° C、第一次向左拐73°,第二次向右拐107° D、第一次向左拐32°,第二次向左拐148°12. 如图,将一副三角板按如图放置,则下列结论:①∠1=∠3;②∠CAD+∠2=180°;③如果∠2=35°,则有BC∥AD;④∠4+∠2=75°.其中正确的序号是( ) A、①②③④ B、①②④ C、①②③ D、①③④
A、①②③④ B、①②④ C、①②③ D、①③④二、填空题(本大题共7小题,每题4分,共28分,将答案填在答题卡对应的位置上)
-
13. 如图,∠2的同旁内角是 .
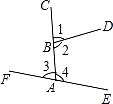 14. 如图,利用直尺和三角尺过直线外一点画已知直线的平行线,这种画法依据的是 .
14. 如图,利用直尺和三角尺过直线外一点画已知直线的平行线,这种画法依据的是 . 15. 已知(x+3)2+ =0,则x+y=.16. 把命题“等边三角形的三个内角都等于60°”写成“如果…那么…”的形式为 .17. 已知x没有平方根,且|x|=27,则x的立方根为 .18. 如图,已知AB∥CD , ∠PAQ=2∠BAQ , ∠PCD=3∠QCD , ∠P=75°,则∠AQC= .
15. 已知(x+3)2+ =0,则x+y=.16. 把命题“等边三角形的三个内角都等于60°”写成“如果…那么…”的形式为 .17. 已知x没有平方根,且|x|=27,则x的立方根为 .18. 如图,已知AB∥CD , ∠PAQ=2∠BAQ , ∠PCD=3∠QCD , ∠P=75°,则∠AQC= .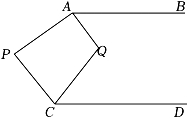 19. 观察下列各式:
19. 观察下列各式:=2;
=3;
=4;
=5;
…
用字母n表示出一般规律是 . (n为不小于2的整数)
三、解答题(本大题共6小题,共74分解答应写出文字说明、证明过程或推演步骤)
-
20. 计算题:(1)、x2=32;(2)、(﹣2)3×﹣×()2+ .21. 如图,网格中每个小正方形的边长均为1,点A、B、C均在小正方形的顶点,把三角形ABC平移得到三角形A1B1C1 , 使C点的对应点为C1 .
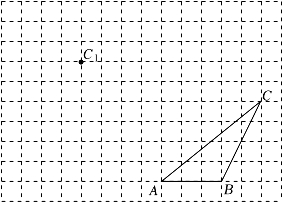 (1)、请在图中画出三角形A1B1C1 .(2)、连接AB1、BB1 , 直接写出三角形ABB1的面积为 .22. 如图,FG∥CD , ∠1=∠3,∠B=50°,求∠BDE的度数,请把下面的解答过程补充完整:
(1)、请在图中画出三角形A1B1C1 .(2)、连接AB1、BB1 , 直接写出三角形ABB1的面积为 .22. 如图,FG∥CD , ∠1=∠3,∠B=50°,求∠BDE的度数,请把下面的解答过程补充完整: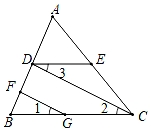
解:∵FG∥CD(已知),
∴∠1=▲ ( )
又∵∠1=∠3(已知),
∴∠3= ▲ (等量代换),
∴BC∥ ▲ ( ),
∴∠B+ ▲ =180°( ),
又∵∠B=50°(已知),
∴∠BDE= ▲ .
23.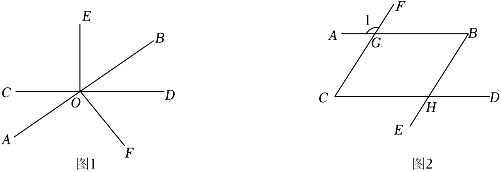 (1)、如图1,已知,直线AB、CD相交于点O , 过点O作OE⊥CD , OF⊥AB , 若∠AOC=32°,求∠EOF的度数.(2)、如图2已知∠1+∠C=180°,CF∥BE . 求证:∠B=∠C .24. 如图,直线CD、EF交于点O , OA , OB分别平分∠COE和∠DOE , 已知∠1+∠2=90°.
(1)、如图1,已知,直线AB、CD相交于点O , 过点O作OE⊥CD , OF⊥AB , 若∠AOC=32°,求∠EOF的度数.(2)、如图2已知∠1+∠C=180°,CF∥BE . 求证:∠B=∠C .24. 如图,直线CD、EF交于点O , OA , OB分别平分∠COE和∠DOE , 已知∠1+∠2=90°.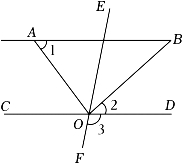 (1)、试说明AB∥CD的理由;(2)、若∠2:∠3=2:5,求∠BOF的度数.25. 已知:直线EF分别与直线AB , CD相交于点G , H , 并且∠AGE+∠DHE=180°.
(1)、试说明AB∥CD的理由;(2)、若∠2:∠3=2:5,求∠BOF的度数.25. 已知:直线EF分别与直线AB , CD相交于点G , H , 并且∠AGE+∠DHE=180°.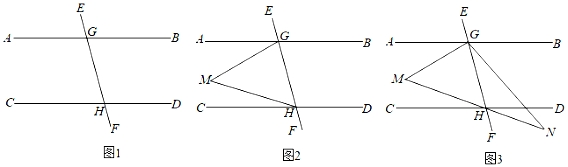 (1)、如图1,求证:AB∥CD;(2)、如图2,点M在直线AB , CD之间,连接GM , HM , 求证:∠M=∠AGM+∠CHM;(3)、如图3,在(2)的条件下,射线GH是∠BGM的平分线,在MH的延长线上取点N , 连接GN , 若∠N=∠AGM , ∠M=∠N+∠FGN , 求∠MHG的度数.
(1)、如图1,求证:AB∥CD;(2)、如图2,点M在直线AB , CD之间,连接GM , HM , 求证:∠M=∠AGM+∠CHM;(3)、如图3,在(2)的条件下,射线GH是∠BGM的平分线,在MH的延长线上取点N , 连接GN , 若∠N=∠AGM , ∠M=∠N+∠FGN , 求∠MHG的度数.