人教版(贵州地区)初中数学2023-2024学年八年级上学期期末模拟卷(一)
试卷更新日期:2023-12-18 类型:期末考试
一、选择题
-
1. 下列算式中,结果等于a6的是( )A、a4 +a2 B、a2+a2+a2 C、a2·a3 D、a2·a2·a22. 下面的计算正确的是( )A、(a+b)2=a2+b2 B、(a3)2=a6 C、a2+a3=2a5 D、(3a)2=6a23. 下列因式分解正确的是( )A、 B、 C、 D、4. 计算的结果为 ( )A、 B、 C、 D、5. 下列每组数分别是三根木棒的长度,能用它们摆成三角形的是( )A、3cm,4cm,8cm B、8cm,7cm,15cm C、5cm,5cm,11cm D、13cm,12cm,20cm6. 使分式有意义的条件是( )A、 B、 C、 D、7. 如图,将一个五边形ABCDE沿虚线裁去一个角后得到的多边形ABCDGF的内角和为( )
 A、180° B、360° C、540° D、720°8. 如图(1),边长为的正方形剪去边长为2的正方形得到①、②两部分,再把①、②两部分拼接成图(2)所示的长方形,根据阴影部分的面积不变,你能验证的结论是( )
A、180° B、360° C、540° D、720°8. 如图(1),边长为的正方形剪去边长为2的正方形得到①、②两部分,再把①、②两部分拼接成图(2)所示的长方形,根据阴影部分的面积不变,你能验证的结论是( ) A、 B、 C、 D、9. 若关于的分式方程有增根,则增根为( )A、 B、 C、 D、10. 如图,在△ABC中,∠ABC和∠ACB的平分线相交于点O , 过O点作EF∥BC交AB于点E , 交AC于点F , 过点O作OD⊥AC于D , 下列四个结论.①EF=BE+CF;②∠BOC=90°+∠A;③点O到△ABC各边的距离相等;④设OD=m , AE+AF=n , 则S△AEF=mn , 正确的结论有( )个.
A、 B、 C、 D、9. 若关于的分式方程有增根,则增根为( )A、 B、 C、 D、10. 如图,在△ABC中,∠ABC和∠ACB的平分线相交于点O , 过O点作EF∥BC交AB于点E , 交AC于点F , 过点O作OD⊥AC于D , 下列四个结论.①EF=BE+CF;②∠BOC=90°+∠A;③点O到△ABC各边的距离相等;④设OD=m , AE+AF=n , 则S△AEF=mn , 正确的结论有( )个. A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 在实数范围内分解因式: .12. 已知 , , 求的值是 .13. 若一扇窗户打开后,用窗钩将其固定,主要运用的几何原理是 .14. 若关于的分式方程无解,则的值是 .15. 若一个等腰三角形的两边长分别为4和10,则这个三角形的周长 .16. 关于的分式方程的解为正整数,且关于的不等式组的解集为 , 则满足条件的所有整数之和为 .17. 如图,已知∠B+∠C=150°,则∠A+∠D+∠E+∠F等于 (度).
 18. 如图,点A在DE上,△ABC≌△EDC,若∠BAC=55°,则∠ACE的大小为
18. 如图,点A在DE上,△ABC≌△EDC,若∠BAC=55°,则∠ACE的大小为
三、计算题
-
19. 因式分解:(1)、4ab-2a2b;(2)、25x2-9y2;(3)、2a2b-8ab2+8b3;(4)、x2(x-3)+9(3-x).20. 先化简,再求值:(a+b)(a-b)+a(2b-a),其中a=3,b=-2.21. 解方程.(1)、;(2)、 .
四、解答题
-
22. 在平面直角坐标系中,△ABC的三个顶点在格点上(每个方格的边长均为1个单位长度).

⑴请画出△ABC关于原点对称的图形△A1B1C1 , 并写出B1点的坐标.
⑵将△ABC绕点B逆时针旋转90°,画出旋转后得到的△A2B2C2;
⑶求(2)中点A移动的距离.
23. 如图,在中, , 将边绕点逆时针旋转得到 , 过点作 , 交的延长线于点 .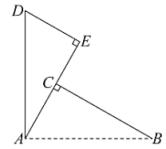
求证:
(1)、;(2)、 .24. 如图,在△ABC中,AD⊥BC,AE平分∠BAC,∠B=70°,∠C=34°,求∠DAE的度数.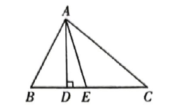
五、综合题